Introducción
Las variables hidrológicas, entre ellas la precipitación, temperatura, infiltración, etcétera, presentan una alta variabilidad espacial y temporal en función del esquema general de circulación atmosférica y de un conjunto de factores locales como la orografía, el efecto del viento en la superficie, pendiente y orientación del terreno (Álvarez, 2011); ello condiciona los ciclos agrícolas y forestales y, por ende, el desarrollo de la flora y la fauna; además, influye en la producción de bienes y servicios, por lo tanto, en la economía.
El registro de estas variables se realiza comúnmente en estaciones con instrumentos de medición discreta y de forma puntual con pluviómetros, pluviógrafos, disdrómetros, etcétera y de forma espacial con radar y satélite, con distintos intervalos de tiempo (Maggioni y Massari, 2018; Haberlandt, 2008). Así, para medir la precipitación existen distintas redes de medición de lluvia de forma puntual como espacial con intervalos de medición desde 1 minuto hasta 24 horas (Plouffe et al., 2015). Indistintamente del equipo de medición, y del intervalo de tiempo, en este proceso existe asociada cierta incertidumbre (García et al., 2014).
Para emplear dicha información en aplicaciones ingenieriles (pronósticos, balances hídricos, extrapolación de variables, proceso lluvia-escurrimiento, diseño de obras hidráulicas, etcétera), generalmente es necesario obtener un valor medio que sea representativo de la zona de estudio (cuencas o subcuencas hidrológicas); para ello, existen distintos métodos de uso tradicional (aritmético, polígonos de Thiessen e isoyetas) (Chow et al., 1994). En otros casos, es útil el valor de dicha variable en un punto o puntos distintos al de medición, en dicho proceso se debe realizar la distribución espacial de la variable hidrológica sobre la zona de interés, empleando técnicas de interpolación (Thiessen, inverso de la distancia, Kriging, etcétera) a partir de la información disponible de forma puntual (He et al., 2005). En el caso de la lluvia, consiste en construir por ejemplo, una superficie de precipitación o campo de tormenta (Cisneros et al., 1998); dicha información es de gran utilidad para emplearla en el proceso lluvia-escurrimiento, en el primer caso para modelos de parámetros agregados y semidistribuidos; en el segundo en modelos de parámetros distribuidos (Ruelland et al., 2008; Mendez y Calvo, 2016).
El análisis de variables hidrológicas y en especial la lluvia, se ha estudiado ampliamente empleando valores medios, para ello, el método más utilizado es el de los polígonos de Thiessen y en menor medida el método de las isoyetas, a pesar de considerarse más preciso (Chua y Brass, 1982; Damant et al., 1983). En cuanto a los métodos de distribución espacial de la lluvia, debido a su facilidad de aplicación, el método inverso de la distancia tiene buena aceptación, por otro lado, los métodos estadísticos cada día tienen mayor peso, en particular el método de Kriging ordinario (Lu y Wong, 2008; Cisneros et al., 1998). El principio básico de la mayoría de las técnicas de interpolación, consiste en predecir el valor de la variable en un punto o área de interés, a partir de valores muestrales vecinos, empleando factores de ponderación espacial (Damant et al., 1983; Plouffe et al., 2015). En este contexto, el factor de ponderación de un valor observado decrece a medida que la distancia en relación con el punto a predecir se incrementa (Mendez y Calvo, 2016).
Debido a ello, hoy en día es relativamente sencillo realizar dichos procesos con el empleo de Sistemas de información Geográfica (SIG), pero es un proceso repetitivo con el cual se genera una gran cantidad de información. Dado que la información generalmente, se utilizará en otras aplicaciones (modelos hidrológicos e hidráulicos), ello se convierte en un proceso un tanto complicado, ya que es necesario intercambiar y adaptar información entre las distintas plataformas (Goovaerts, 2000).
De esta manera, el objetivo de este trabajo es el desarrollo de un código de cálculo en el cual se implementan distintos métodos de interpolación (Thiessen, inverso de la distancia, Kriging ordinario) para realizar la distribución espacial de variables hidrológicas, mediante el empleo de archivos en formato ASCII, lo que facilita el intercambio de información con SIG. Además, permite determinar la variable media de un área de estudio con los métodos tradicionales (aritmético, polígonos de Thiessen) y a partir de los datos de la distribución espacial hecha con los métodos de interpolación. Los resultados de dicho proceso, son el insumo para otros modelos, entre ellos, modelos lluvia-escurrimiento concentrados y distribuidos. Dichos desarrollos se aplicaron y evaluaron en un dispositivo físico de laboratorio y en una cuenca hidrológica, con características fisiográficas y de la variable hidrológica, en este caso de la lluvia, muy variadas.
Desarrollo
Para la aplicación y validación de los métodos implementados, se utilizará un dispositivo experimental y una cuenca hidrológica; en ambas se dispone con la información requerida, esto es, características fisiográficas, ubicación de los instrumentos de medición y registros de precipitación.
Mesa hidrológica
La mesa hidrológica consiste en un dispositivo experimental que permite reproducir algunos fenómenos del ciclo hidrológico, entre ellos, la lluvia, escurrimiento superficial y la infiltración; está instrumentado con cinco pluviómetros distribuidos de forma uniforme (Figura 1 y Tabla 1), seis sensores de presión hidrostática por peso (cinco para medir lluvia en diferentes puntos de la cuenca y uno para medir la carga hidráulica en un vertedor rectangular ubicado en la salida de la cuenca y con ello el escurrimiento superficial y bajo ciertas circunstancias el escurrimiento subterráneo producto de la infiltración) y un sensor de nivel por conductividad para medir el nivel de agua en los cauces; no se dispone de la instrumentación para medir la infiltración. La mesa hidrológica tiene una longitud de 2 m de longitud y 1 m de ancho, por lo que el área de aportación es de 2 m2, longitud y pendiente del cauce principal de 2.75 m y 8%, respectivamente (Aragón et al., 2017).
Tabla 1 Registros de la lluvia sintética
| Estación | x (m) | y (m) | z (m) | P (mm) |
|---|---|---|---|---|
| 1 | 0.525 | 0.185 | 0.082 | 3.7 |
| 2 | 0.775 | 0.895 | 0.120 | 49.7 |
| 3 | 0.335 | 0.720 | 0.093 | 18.0 |
| 4 | 0.730 | 1.630 | 0.120 | 91.7 |
| 5 | 0.300 | 1.590 | 0.144 | 5.3 |
En dicho dispositivo se generaron distintos patrones de lluvia sintética con diferentes magnitudes, intensidades y duraciones, todas registradas por los cinco pluviómetros; el registro más desfavorable se muestra en la Tabla 1. Para este evento no se midió la infiltración y tampoco el escurrimiento subterráneo.
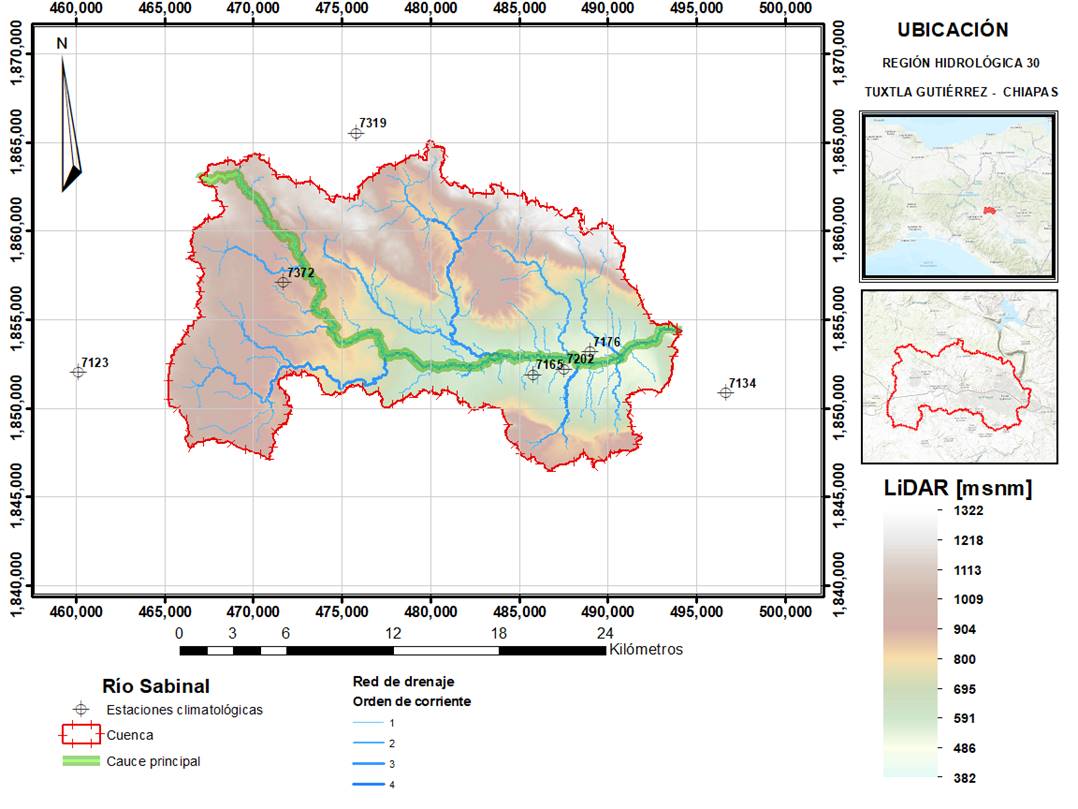
Cuenca del río Sabinal
La cuenca del río Sabinal se encuentra ubicada en el estado de Chiapas en el sureste de la República Mexicana (Figura 2) y pertenece a la región hidrológica 30 Grijalva-Usumacinta y a la región hidrológica-administrativa XI Frontera sur. Abarca porciones de cinco municipios, entre ellos, la capital del estado de Chiapas, Tuxtla Gutiérrez, que aporta casi 40% del área. La cuenca del río Sabinal tiene un área de aportación de 340.27 km2, longitud y pendiente del cauce principal de 40.7 km y 2%, respectivamente.
En la zona urbana de dicha cuenca, las inundaciones son recurrentes debido a lluvias intensas provocadas generalmente por eventos hidrometeorológicos, como los ciclones tropicales; uno de estos eventos, el ciclón tropical Larry, provocó precipitaciones importantes del 4 al 7 de octubre de 2003 en la parte alta de la cuenca del río Sabinal, sobre todo el día 5 de octubre, cuyas láminas de lluvia acumulada en 24 horas fueron registradas por siete estaciones climatológicas (Tabla 2).
Tabla 2 Registros de lluvia acumulada en 24 horas. 5/octubre/2003
| Clave | Estación | x (m) | y (m) | z (msnm) | P (mm) |
|---|---|---|---|---|---|
| 7123 | Ocozocoautla | 460,148.41 | 1,852,025.10 | 838 | 120.0 |
| 7134 | Puente Colgante | 496,685.09 | 1,850,859.54 | 418 | 47.5 |
| 7165 | Tuxtla Gutiérrez (SMN) | 485,792.43 | 1,851,903.89 | 570 | 18.0 |
| 7176 | Tuxtla Gutiérrez (CFE) | 489,043.90 | 1,853,196.24 | 532 | 46.0 |
| 7202 | Tuxtla Gutiérrez (DGE) | 487,561.00 | 1,852,212.52 | 543 | 19.1 |
| 7319 | San Fernando | 475,831.78 | 1,865,530.70 | 950 | 131.0 |
| 7372 | Berriozábal | 471,730.28 | 1,857,106.24 | 890 | 225.5 |
Métodos de interpolación
Para realizar la distribución espacial de una variable hidrológica se implementaron el método de los polígonos de Thiessen (vecino cercano), el método del inverso de la distancia y el método de Kriging ordinario. Además, es posible calcular el valor medio de dicha variable a partir de datos puntuales con el método aritmético y el método de los polígonos de Thiessen y a partir de información distribuida espacialmente.
Kriging ordinario
El estudio de fenómenos con correlación espacial, por medio de métodos geoestadísticos surgió con el propósito de predecir valores de las variables en sitios no muestreados, lo cual se puede lograr en dos etapas (Gotway, 1991; Cressie, 1985). La primera consiste en un análisis estructural con la finalidad de describir la correlación entre puntos muestrales en el espacio; la segunda, hacer la predicción en puntos de la región no muestrales por medio de la técnica Kriging. Esta técnica engloba un conjunto de métodos que se fundamentan en la minimización del error cuadrático medio de predicción; este trabajo se enfoca en uno de ellos, el método de Kriging ordinario, el cual propone que el valor de la variable en un punto no muestral
Donde
donde:
La varianza del error de predicción se puede obtener como:
donde
Los valores de
Todos los modelos teóricos de semivariograma tienen tres parámetros
Donde
Inverso de la distancia
El método del inverso de la distancia supone que con el aumento de la distancia, el valor de la variable entre dos puntos implica menor similitud, siempre y cuando la variable sea continua en el espacio, ello justifica el uso de factores de ponderación dependiente de una función inversa de la distancia. Lo anterior se puede expresar como (Lu y Wong, 2008):
Donde
Polígonos de Thiessen
El método de los polígonos de Thiessen consiste en extrapolar la precipitación registrada en un punto muestral al conjunto de puntos de la cuenca que tengan a ese punto muestral como el más cercano (Tabios III y Salas, 1985).
Evaluación de los métodos
La evaluación de los métodos de interpolación descritos anteriormente, se realiza por medio de regresión lineal y correlación cruzada; esta última consiste en evaluar el error en cada punto de registro entre el valor medido respecto al valor extrapolado con el resto de registros (Isaaks y Srivastava, 1989); este procedimiento se aplica sobre cada uno de los valores registrados, es decir, realizando tantas interpolaciones como valores medidos se tengan. De esta manera, del error
donde
Precipitación media
El valor medio de una variable hidrológica en una zona de estudio, representa el valor medio repartido de forma uniforme en toda el área; una de las finalidades de dicho valor, es utilizarlo en modelos agregados. Para determinarlo, tradicionalmente se emplean entre otros, el método aritmético y el método de los polígonos de Thiessen; adicionalmente, si la información proviene de mediciones o datos en forma espacial se utiliza un método denominado malla regular.
Método aritmético
El método aritmético es el promedio de los valores de la variable registrada en la cuenca (Singh, 1988).
donde
Polígonos de Thiessen
La precipitación media con el método de los polígonos de Thiessen se calcula como una ponderación de la precipitación de las estaciones respecto al área de influencia, como (Tabios III y Salas, 1985):
Donde
Malla regular
El valor medio de una variable hidrológica con datos a partir de un campo de precipitaciones se calcula como (Álvarez, 2011; Plouffe et al., 2015):
donde
Resultados y discusión
La aplicación de los diferentes métodos de interpolación implementados para distribuir de forma espacial la lluvia en las cuencas de estudio y el cálculo de precipitación media con los distintos métodos, se presenta en las siguientes secciones; para ello, se realizó un análisis del tamaño de celda para la discretización de la zona de estudio y del exponente
Antes de realizar la distribución de la precipitación en la mesa hidrológica (caso 1) y la cuenca del río Sabinal (caso 2), primero se calculó la precipitación media de las cuencas en estudio con los métodos tradicionales (Tabla 3); dado que no fue posible calcular la lluvia media con los datos medidos (lluvia y escurrimiento superficial; no se midió la infiltración ni el escurrimiento subterráneo), esta se estimó con el método de las isoyetas, considerado el más preciso, y por tanto, como valor de referencia para este trabajo. De ello se desprende que, el método de los polígonos es más exacto que el método aritmético; este último tiene diferencias de hasta 28.3% respecto al método de las isoyetas en el caso 2.
Tabla 3 Precipitación media a partir de información puntual y distribuida
| Caso 1 | Caso 2 | |||
|---|---|---|---|---|
| Método | Pm (mm) | ER (%) | Pm (mm) | ER (%) |
| Aritmético | 33.7 | 5.25 | 86.73 | 28.30 |
| Polígonos de Thiessen | 31.9 | 0.22 | 122.03 | 0.88 |
| IDW | 32.0 | 0.00 | 120.91 | 0.04 |
| Kriging ordinario | 33.0 | 3.16 | 112.52 | 6.98 |
| Isoyetas (exacto) | 32.0 | - | 121.0 | - |
Posteriormente, se discretizaron las zonas de estudio con tamaños de celda distintos (Tabla 4 y Tabla 5), además se calculó el área de la cuenca y la precipitación media con el método de los polígonos de Thiessen (M1), inverso de la distancia (M2), Kriging ordinario (M3).
Tabla 4 Variables de discretización de la mesa hidrológica
| Pm (mm) | |||||
|---|---|---|---|---|---|
| Tamaño (m) | Número | A (m2) | M1 | M2 | M3 |
| 0.001 | 2,006,022 | 2.01 | 31.9 | 32.0 | 33.0 |
| 0.0025 | 320,760 | 2.00 | 31.9 | 32.0 | 33.0 |
| 0.005 | 80,080 | 2.00 | 31.8 | 31.9 | 32.9 |
| 0.010 | 20,020 | 2.00 | 31.6 | 31.7 | 32.9 |
| 0.025 | 3,212 | 2.01 | 31.2 | 31.3 | 32.6 |
| 0.050 | 792 | 1.98 | 30.0 | 30.2 | 32.0 |
| 0.10 | 198 | 1.98 | 28.1 | 28.6 | 31.2 |
| 0.25 | 28 | 1.75 | 26.3 | 26.1 | 28.8 |
| Media: | 1.97 | 30.4 | 30.5 | 32.0 | |
Tabla 5 Variables de discretización de la cuenca del río Sabinal
| Pm (mm) | |||||
|---|---|---|---|---|---|
| Tamaño (m) | Número | A (km2) | M1 | M2 | M3 |
| 25 | 544,427 | 340.27 | 122.0 | 120.9 | 112.5 |
| 50 | 136,143 | 340.36 | 122.1 | 120.9 | 112.5 |
| 100 | 34,012 | 340.12 | 122.2 | 121.0 | 112.6 |
| 250 | 5,446 | 340.38 | 122.5 | 121.4 | 112.7 |
| 500 | 1,359 | 339.75 | 122.3 | 121.3 | 112.6 |
| 1,000 | 340 | 340.00 | 124.5 | 123.1 | 113.4 |
| 2,500 | 53 | 331.25 | 119.5 | 121.6 | 113.9 |
| 5,000 | 15 | 375.00 | 130.3 | 129.6 | 118.2 |
| Media: | 343.39 | 123.2 | 122.5 | 113.6 | |
En la mesa hidrológica, el área de aportación y la precipitación media es poco sensible al tamaño de la celda a excepción del tamaño de celda de 0.10 m y 0.25 m, ya que presenta errores relativos de hasta 18.5%. En la cuenca del río Sabinal, las áreas de aportación para las discretizaciones de 2,500 m y 5,000 m, se pueden considerar como no representativas, ya que presenta diferencias mayores a 10%, en cambio, el error relativo de la precipitación media, es de hasta 7.7%. En este sentido, considerando que entre menor es el tamaño de celda se tiende a la solución exacta, para los análisis se utilizó un tamaño de celda de 0.001 m en la mesa hidrológica y de 25 m en la cuenca del río Sabinal.
Con la discretización propuesta, se propusieron exponentes
Tabla 6 Precipitación media en función del exponente
| Pm (mm) | ||
|---|---|---|
| b | Caso 1 | Caso 2 |
| 1 | 33.41 | 93.07 |
| 2 | 32.96 | 104.55 |
| 3 | 32.66 | 111.89 |
| 4 | 32.47 | 115.72 |
| 6 | 32.24 | 118.93 |
| 8 | 32.12 | 120.13 |
| 10 | 32.05 | 120.72 |
| 11 | 32.03 | 120.91 |
| 12 | 32.01 | 121.05 |
| 13 | 32.00 | 121.20 |
| 15 | 31.98 | 121.35 |
| 20 | 31.50 | 121.60 |
En relación con el método de Kriging ordinario, para cada caso se realizó el ajuste de los distintos modelos de variogramas teóricos (Ecuaciones 5-7); los mejores ajustes se obtuvieron con los modelos esférico y Gaussiano para la mesa hidrológica y la cuenca del río Sabinal, respectivamente; bajo las consideraciones anteriores en la Figura 3 se presenta la distribución espacial de la lluvia en la mesa hidrológica y la correspondiente a la cuenca del río Sabinal en la Figura 4.
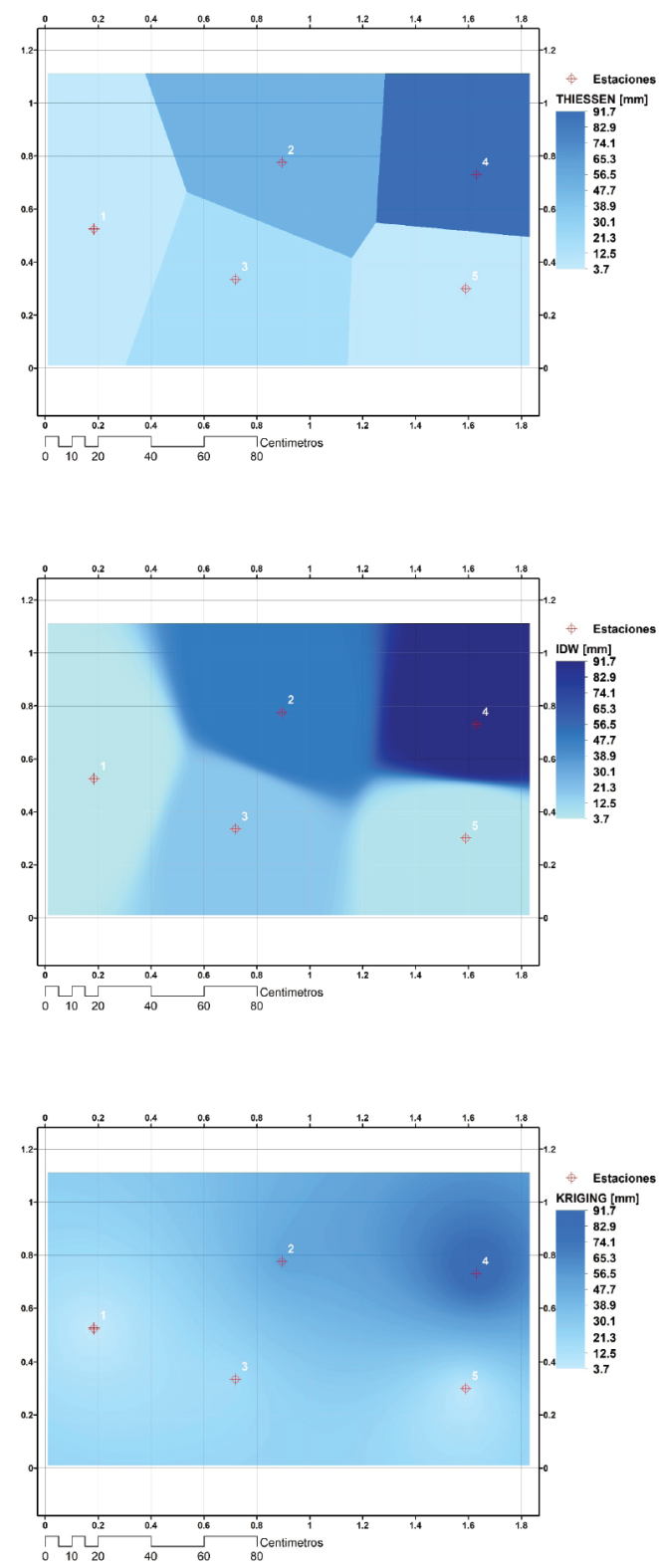
Figura 3 Distribución espacial de la precipitación en la mesa hidrológica: a) polígonos de Thiessen, b) inverso de la distancia y c) Kriging ordinario
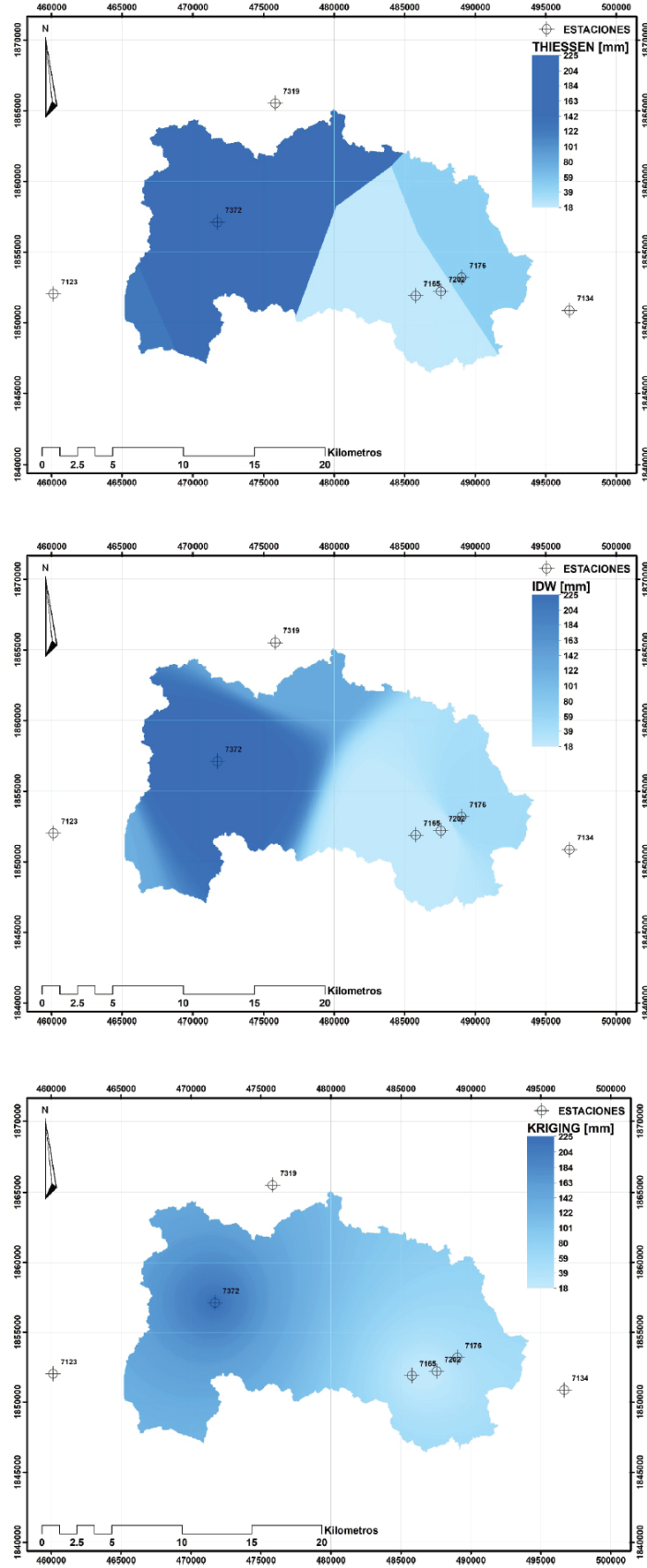
Figura 4 Distribución espacial de la precipitación en la cuenca del río Sabinal: a) polígonos de Thiessen, b) inverso de la distancia y c) Kriging ordinario
A partir de dicha distribución espacial de la precipitación, se calculó también la precipitación media (Ecuación 15 y Tabla 3); si se comparan los métodos de interpolación solamente con la precipitación media como referencia (calculada con el método de las isoyetas), en ambos casos, el método inverso de la distancia es el mejor.
Para evaluar la actuación de cada uno de los métodos de interpolación en la distribución espacial de la precipitación, se realizó la correlación cruzada; en el caso de la cuenca del río Sabinal, solamente se utilizaron las estaciones ubicadas dentro de la cuenca (7165, 7176, 7202 y 7372). Para ello, se determinó el error (valor medido menos el valor estimado) en cada uno de los puntos de medición correspondientes; los resultados se muestran en la Tabla 7; para la aplicación del método de Kriging ordinario; los parámetros del modelo teórico de semivariograma (Ecuaciones 5-7) se determinaron mediante regresión no lineal, para ello, primero se determinaron en cada caso, los semivariogramas experimentales (Ecuación 8).
Tabla 7 Errores obtenidos en la correlación cruzada
| Método | Caso | EMC (mm) | EMA (mm) | EM (mm2) |
|---|---|---|---|---|
| Polígonos de Thiessen | 1 | 3,426.6 | 50.1 | -2.9 |
| 2 | 2,414.1 | 30.9 | 30.4 | |
| IDW | 1 | 3,443.6 | 50.5 | -3.3 |
| 2 | 2,510.7 | 33.9 | 27.5 | |
| Kriging ordinario | 1 | 2,398.7 | 42.5 | -9.0 |
| 2 | 1,392.0 | 25.3 | 22.5 |
Así, al comparar los diferentes errores, se desprende que para la mesa hidrológica, el mejor método de distribución espacial de la lluvia por decisión dividida corresponde al método de Kriging ordinario (dos de tres) y para la cuenca del río Sabinal por decisión unánime también corresponde al método de Kriging ordinario (tres de tres).
Además, para conocer la bondad de los métodos de interpolación (M1: método de los polígonos de Thiessen, M2: inverso de la distancia, M3: Kriging ordinario) en la estimación de variables, en las Figuras 5 y 6 se presenta la correlación lineal existente entre la lluvia medida y la lluvia estimada por dichos métodos, para ambos casos, respectivamente. Se puede observar que en la mesa hidrológica, la correlación es baja, en cambio, en la cuenca del río Sabinal, dicha correlación es muy buena; en ambos casos, como es de esperar, la mayor correlación la presenta el método de interpolación Kriging ordinario (M3).
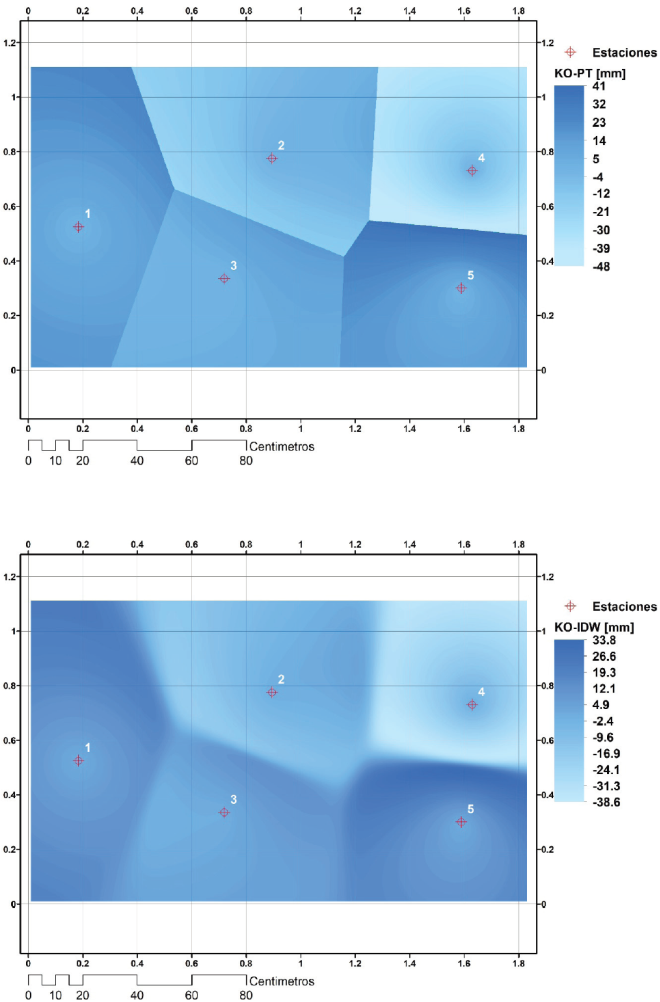
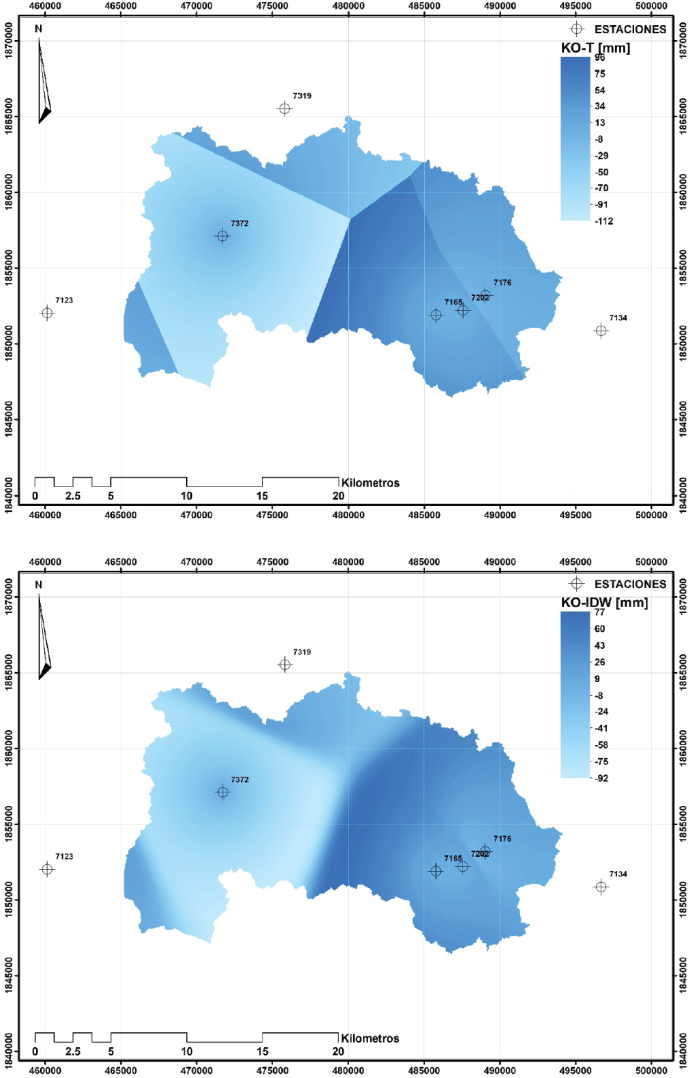
Finalmente, para conocer en qué zonas de las cuencas se presentan las mayores diferencias en la precipitación estimada, se determinó el error absoluto en cada celda (valor medido menos el valor estimado); se consideró que la distribución espacial con el método de Kriging corresponde a los valores medidos o más precisos. Los resultados se muestran en la Figuras 7 y 8 (KO, corresponde al método de Kriging ordinario, PT al método de los polígonos de Thiessen e IDW al método inverso de la distancia).
La evaluación de los métodos mediante la precipitación media, correlación cruzada y regresión lineal, sin duda ofrecen buenos resultados, así lo indican los estimadores empleados, pero las diferencias de láminas de lluvias entre el método de Kriging ordinario (empleado como de referencia) en relación con el método de los polígonos de Thiessen e inverso de la distancia, en algunas áreas se observan diferencias importantes de hasta 50%; tales diferencias podrían tener repercusiones, si no a nivel de cuenca, sí a nivel de subcuencas, sobre todo en el escurrimiento producido por la lluvia.
Conclusiones
En este trabajo se desarrolló un código de cálculo y se implementaron tres métodos de interpolación de variables (polígonos de Thiessen, inverso de la distancia y Kriging ordinario) para la distribución espacial de variables hidrológicas y el valor medio de la misma con dos métodos tradicionales, en ambos casos, a partir de valores puntuales; además, permite calcular el valor medio a partir de datos distribuidos en celdas en que se discretiza la zona de estudio, por lo que lo convierte en una herramienta eficiente, amigable y de gran utilidad y apoyo en distintas áreas de interés. Dicha herramienta, se puede aplicar en cualquier área y con cualquier variable, en especial las hidrológicas, como en este caso, que se realizaron aplicaciones para determinar tanto la distribución espacial y el valor de la precipitación en un dispositivo físico en el laboratorio (mesa hidrológica) y la cuenca del río Sabinal con características fisiográficas muy distintas (varios ordenes de magnitud) y patrones, magnitudes, duraciones e intensidad de lluvias diferentes.
A partir de dichas aplicaciones, se realizó la distribución espacial de la lluvia con los distintos métodos y la precipitación media a partir de datos puntuales (métodos tradicionales) y de las celdas. Con dicha información se realizó una evaluación de los diferentes métodos.
El cálculo de la precipitación media con datos puntuales y aquellos obtenidos con los métodos de extrapolación se evaluó utilizando la precipitación media calculada con el método de las isoyetas como referencia; ello indica que en el caso de los métodos tradicionales, el mejor corresponde al método de los polígonos de Thiessen; en cambio, con los métodos de interpolación correspondió al método inverso de la distancia. La evaluación de los métodos de interpolación mediante correlación cruzada y regresión lineal, concluye que el método de Kriging ordinario es un buen estimador en ambas aplicaciones.
A pesar de que la evaluación mediante la precipitación media, correlación cruzada y regresión lineal ofrece buenos resultados para los métodos correspondientes, al analizar las láminas de lluvia que cada método proporciona, se pudo constatar que existen áreas en donde las diferencias son de hasta 50% respecto al otro, ello puede traer consecuencias si no a nivel de cuenca, sí a nivel de subcuencas, dichas diferencias de lámina de lluvia pueden generar escurrimientos importantes.
Además, se realizó un análisis de sensibilidad del tamaño de celda con que se discretiza la zona de estudio y del exponente en el método del inverso de la distancia. Tanto el área de la cuenca como la precipitación media son ligeramente sensibles al tamaño de la celda, por lo que se sugiere, utilizar el tamaño de celda menor posible desde el punto de vista práctico, ya que a menor tamaño mayor precisión, pero también más elementos producto de la discretización, por lo tanto, mayor tiempo de cálculo. Por otra parte, en la práctica, es bastante común utilizar un exponente en el método inverso de la distancia de dos, lo cual lo convierte en el método inverso de la distancia al cuadrado, sin embargo, en ambas aplicaciones el menor error de la precipitación media se logró con exponentes mayores a 10 (13 en el dispositivo físico y 11 en la cuenca hidrológica); en este sentido, entre mayor es el exponente, mayor pérdida de información conforme aumenta la distancia, por lo que es de esperarse que, entre más separadas se encuentren las estaciones, dicho valor será menor y viceversa.











 nueva página del texto (beta)
nueva página del texto (beta)