1 Introduction
The quantity of information that society produces is affected since human capacity to categorize it is limited. Thus, Machine Learning has developed algorithms capable of processing great quantities of documents and associate them to certain topics. This type of analysis receives the name of Probabilistic Topic Modeling. In this type of models statistic methods are used to analyze the words of the texts and to identify the groups of words that constitute the topics of which the documents are composed. One of the methods that precedes the statistics, is the Latent Semantic Analysis (LSA) model that applies the algebraic principle of decomposition in singular values, that consists in the factorization of a matrix [19].
Hofmann [15, 16], starting from the LSA model, developed a new algorithm that turned away of linear algebra and centered in the statistic analysis called Probabilistic Latent Semantic Analysis (pLSA). The modification that was introduced to this new study was the creation of topics that is a new relation between words and documents. Words were distributed around the topics where words can be shared and everyone has a different relevance within each document.
As it can be sensed, the topics must be deduced from the text. This method of unsupervised learning uses the iterative algorithm Expectation Maximization (EM) to determine the distribution of the latent variables.
Blei [8] get backs the idea of latent structure of topics and designs a generative model of documents called Latent Dirichlet Allocation (LDA) and is based in the basic concept that a collection of documents presents a logic structure of words that belong, in different proportion, to each of the topics that are responsible for the generation of documents. Instead of directly estimating the distributions words-topics and topics-documents, it uses another approach that is to directly estimate the posterior distribution given by the observed words.
Currently, this algorithm is one of the most simple and mostly used in Topic Modeling.
The main objective of this work is to develop a system based in the Latent Dirichlet Allocation (LDA) model to carry out the task of automatically selecting the corpus words and, based on their frequency in the documents, it would indicate that they may or do not belong to certain topic.
This will be implemented using Serial-Parallel Algorithm (SPA) in C/C++ programming language with parallel programming using OpenMP and in a shared memory architecture.
This document is organized as follows. In section 2, the state of art in the field of topic modeling and LDA. In section 3, the design and development of the LDA model are realized, section 4, results and findings of the application of the LDA model are presented. Finally in section 5, final comments and future work of the research are presented.
2 State of the Art
In this section, the main contributions of works related to the application of topics models and LDA are revised as described below.
The important contributions to the statistical analysis identify certain topic models known as Probabilistic Topic Modeling, that refer to statistical algorithm to discover latent semantic structures of extensive body text. Some interesting language properties, as hierarchical semantic relations between words [8] and the interaction between syntax and semantics [13]. In the technical note of [20], the objective is to review the foundations of Bayesian parameter estimation in the discrete domain, that is necessary to comprehend the internal functioning of text analysis approaches based on topics as Probabilistic Latent Semantic Analysis (PLSA), Latent Dirichlet Allocation (LDA) [6], and other methods of count data mixing
2.1 Topic Modeling
The Latent Dirichlet Allocation (LDA) model is a generative probabilistic model. The basic idea is that the documents to be classified are represented as random mixtures of hidden topics, where each topics is characterized by a distribution of words. The distribution of categories has a priori distribution of Dirichlet, this model is the most commonly used in the following works.
Authors Ruiz and Campos in [25] present a study where they measure the performance of an algorithm that combines non-linear kernels, concurrences of skull shape features, a method of selection of variables and a standard algorithm of dimensionality reduction to characterize and classify malformations caused by primary craniosynostosis. The sorting technique used in this work is that a particular class of skull shapes can be represented through characteristic patterns. The implemented dimensionality reduction model is based on the LDA algorithm. LDA is used as a generative model that samples skull shape features from a mix of geometric topics. The results of that study suggest that the combination of shape descriptor calculations (of the skulls) and LDA technique result in low rates of classification errors.
In the work of Bisgin, Liu, Fang, Xu and Tong in [7], the relationship between medicines and drugs approved by FDA is determined. In this way, each drug is associated to the most probable topic. The model used in the extraction of topic is LDA.
The author Hu in [17] employs unsupervised learning in the study of 2 bible books (proverbs and psalms) due to the shared association of information. The chapters of each book are grouped by content. The model that determines the association between books is LDA algorithm, the extraction of topics of each document identified by the model is used to define a correlation and measure the similarity between both books.
The author Rodríguez in [24], unveils tools that analyze sport videos using computer vision and pattern recognition techniques. Currently, to improve sport results, clubs lay out people in charge of analyzing the matches on their staffs, both their own and those of rival teams, to find patterns in their gameplay and, thus, study the best form to obtain competitive advantages. Once evaluated their right functioning of the algorithm, the next step is to test the model on sport videos and see if it is capable of breaking them down in topics. In the discovery phase, the LDA unsupervised learning method is used to discover activities and interaction in places very crowded.
Authors Dueñas and Velásquez in [10] present an alternative methodology to detect Web trends through the use of information retrieval techniques, topic modeling and opinion mining. Given a set of Websites, topics that are mentioned in the retrieved texts are extracted and later, social networks are used to obtain the opinion of their users in relation to these. LDA is used for the extraction of important topics from the opinions consigned in blogs and news sites.
Seiter, Amft, Rossi, and Tröster in [26] compare the results of three unsupervised models (LDA, n-gram TM, Correlated TM (CTM)), in three data sets of public activities to obtain guidelines for the selection of TM parameters depending on the properties of the set data. In this work, it is determined that the main limitation of the unigram model is that it supposes that all documents are just collections of homogenous words, that is to say, all documents present one unique topic. The experimental results about the selected data set have demonstrated that the LDA proposal in the discovery of information results to be less sensible to noise. The LDA method initially was developed to model discrete data sets, though overall text documents. In the task of modeling a document, LDA handles better than LSI and a mix of unigram models. LSI over adjusts the probabilities of document modeling to determine the topics in a new document. Predictably, the great advance of LDA with LSI was that probabilities are easily allocated to a new document. Its application in documents classification determines that the LDA model can be useful as a screening algorithm to the topic selection function.
The LDA is a robust and generic model that is easily extendable beyond empiric data of a small discussed set. Diverse articles have been published about the application of LDA to a wide range of areas. It has been applied to tasks ranging from fraud screening in telecommunications to error detection in the source code. Despite the wide range of applications, LDA has not been applied to automatic summary of documents, although the possibility is quite feasible. The LDA model has demonstrated to be a a method that allows to assign a class or category to an object to create learning, generating a good separability between classes and a good cohesion within the same class.
Words of documents are the observable variables, meanwhile that the topics, the relation between each document and the topics, the correspondence between each word and topic, are non-explicit distributions. Considering the observed words in a set of documents, the class of topics more likely to have generated the data must be determined. This implies to infer the probability distribution on words associated with each topic and the distribution on the topics of each document.
3 Design and Development of LDA Model
3.1 LDA Generative Model
In LDA (Latent Dirichlet Allocation), if observations are words in documents, each document can be seen as a mix of various topics. In LDA, it is assumed that the distribution of topics has a distribution a priori of Dirichlet [20]:
where
since Dir(p;a) is a function of density, then it is fulfilled:
Which implies that:
3.2 Development of LDA Model
The list of symbols in LDA model to begin the development is described in Table 1.
Table 1 List of symbols used in LDA model
| Variables | Meaning |
| N | Number of words in the corpus. |
| W = {wi} | The corpus, wi denotes a word. |
| Z = {zi} | Latent topics, zi topic assigned to the wordith. |
| W-i = W -{wi} | The corpus excluding Wi. |
| Z-i = Z-{zi} | The corpus excluding Zi. |
| K | Number of topics. |
| V | Number of words (terms) in the vocabulary. |
| D | Number of documents. |
| Nd | Number of of words in the document d. |
| v | Denotes a word (term) in the vocabulary. |
| α | Vector K-dimensional of real positives. |
| β | Vector V-dimensional of real positives. |
| θ | Vector K-dimensional of probabilities. |
| φ | Vector V-dimensional of probabilities. |
The model specifies the following distribution on words within a document:
where p(zi = j) is the probability that the jth topic was chosen to the ith word and p(wi / zi = j) is the probability to choose the word wi come down to topic j.
Table 2 is an example of the distribution of words in a corpus.
Table 2 Distribution of words in a corpus
| Term_1 | Term_2 | Term_3 | Term_4 | Term_5 | |
| Doc_1 | 0.2 | 0.1 | 0.1 | 0.4 | 0.2 |
| Doc_2 | 0.5 | 0.2 | 0.1 | 0.1 | 0.1 |
| Doc_3 | 0.0 | 0.2 | 0.4 | 0.0 | 0.4 |
| Doc_4 | 0.2 | 0.0 | 0.3 | 0.2 | 0.3 |
The probability of
where
Table 3 is an example of the distribution of terms in the topics.
Table 3 Distribution of terms in a corpus
| Term_1 | Term_2 | Term_3 | Term_4 | Term_5 | |
| Top_1 | 0.3 | 0.1 | 0.0 | 0.4 | 0.2 |
| Top_2 | 0.1 | 0.4 | 0.1 | 0.2 | 0.2 |
| Top_3 | 0.0 | 0.2 | 0.4 | 0.3 | 0.1 |
The LDA model introduces a distribution of Dirichlet prior on [20]. The prior to is the following:
The hyperparameters
where
A Dirichlet is introduced prior
Table 4 Distribution of topics in documents
| Top_1 | Top_2 | Top_3 | Top_4 | |
| Doc_1 | 0.4 | 0.2 | 0.1 | 0.3 |
| Doc_2 | 0.8 | 0.0 | 0.2 | 0.0 |
| Doc_3 | 0.3 | 0.2 | 0.1 | 0.4 |
| Doc_4 | 0.0 | 0.3 | 0.4 | 0.3 |
The hyperparameters
Good options for the hyperparameters
The main variables of interest in the model are the distributions of words-topics
In this work, it will be applied an algorithm that uses the Gibbs sampling, a form of chain of Markov Monte Carlo, that is easy to implement and provides a method relatively efficient to extract a set of topics of a great corpus [9, 11].
Gibbs sampling (also known as como la conditional sampling alternation), is a specific form of MCMC, simulates a multidimensional distribution through the sampling of subsets of variables of inferior dimensions, where each subset is conditioned to the value of all the others. The sampling is realized continuously until all sampled values approximate to the destination distribution. The process of Gibbs does not provide direct estimations of
3.3 Gibbs Sampling
To obtain a sample of
On the other hand, it is known that:
and
Using (4), (5) and (3), it is obtained:
Now,
Substituting (11, 12) in (9), it is obtained:
As
But it is known that:
Doing the same as for obtaining (13), we have:
where
Finally using (13, 14, 15, 16), the expression (8) can be written as:
Then:
Using the equalities
it is obtained:
Finally, the estimations of Bayes of the parameters of the function of posterior distribution are:
Table 5 shows how each word in a document is assigned to a topic.
4 Experimental Part
The development of the system LDA will be executed in parallel form, in various processors and cores, so that the time of execution is greatly reduced. In the best parallelization, must exist an independence of data between the tasks, that is to say, a task A does not needs information of the task B to realize its work, and vice verse. However, there exist cases in which the tasks despite of being able to execute in parallel form, need to communicate between them, either message passing or because they share variables, thus, there must exist a mechanism of synchronization [2, 11, 22].
4.1 Programming Language
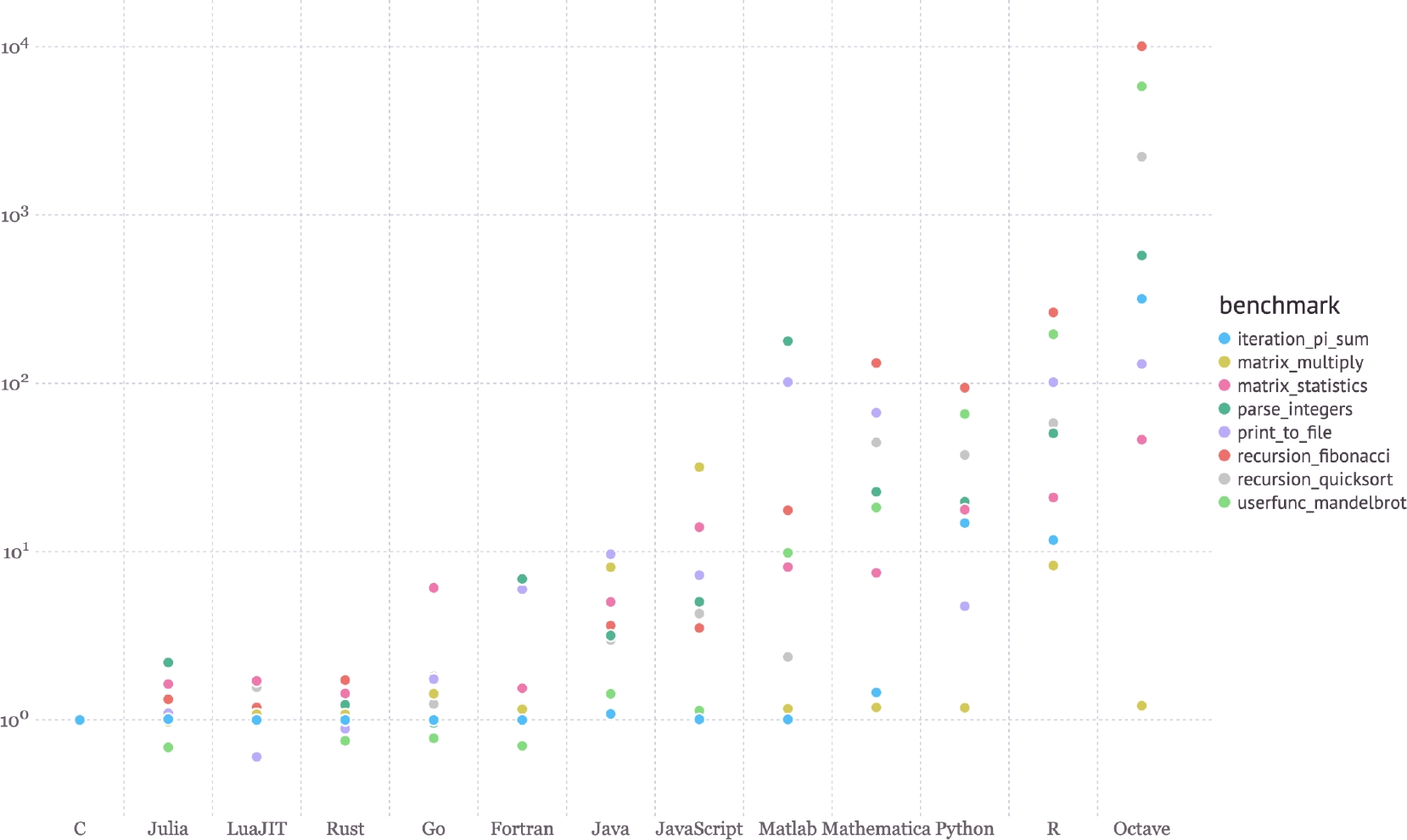
Nowadays it exists a wide variety of programming languages that serve to make parallel or concurrent computing, between them C/C++, Java, Python, Julia, among others stand out. However, what is been looking for the implementation of system LDA is a language of high perfromance. And it was found in the page of Julia [6] the graphic shown in Fig. 14, where different “benchmarks” have been made with different programming languages, and results are compared against C, where it can be clearly appreciated that C is overcome few times regarding its performance. For these reasons it was decided to realize the programming of system LDA in language C/C++.
4.2 Programming of System LDA
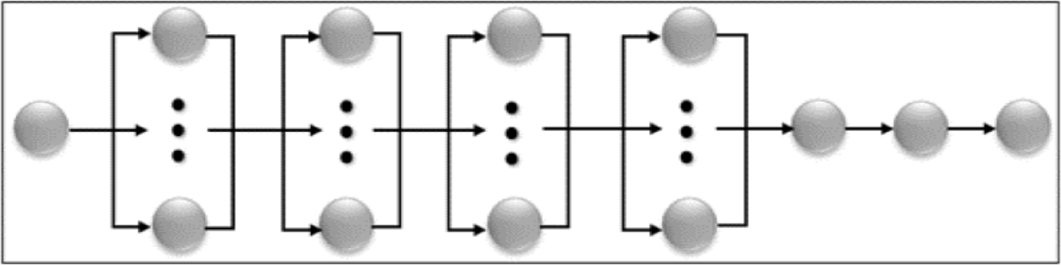
For the programming of system LDA, an Algorithm of type Serial-Parallel (SPA) has been used, which, can be graphically seen in Fig. 2.
To be able to carry out the parallel programming, it has decided to use OpenMP, this due to that in the parallel stages all created threads must share certain variables, and the fact that in MPI this is not possible, makes it to be discarded immediately. Thus, the architecture of memory occupied was the shared memory [4, 5, 3, 21, 27].
4.2.1 Initialization
It is in this stage the initialization of the system, that is to say, here it is defined the quantity of topics for the corpus (k), it is defined the quantity of iterations (iter) for the system sistema LDA, and are calculated the values alfa-beta of the equation.
Once this is done, they must be read and stored, the names of the files that belong to corpus for later load all the vocabulary along with its frequency in a dictionary. When the dictionary is created, all words which frequency in the corpus is less than three are deleted. This is, the words with a frequency very reduced cannot define topics, besides, they would only cause noise in the final results.
Knowing the quantity of files that belong to corpus, and the quantity of words in the dictionary, sonare created two matrices of real numbers; the first represents topics by vocabulary (that will be called ntk), and the second represents the documents by topics (that will be called nkm).
It must have special care in this part, since the created matrices can become very big, for example, if 1,000 topics are chosen, and the vocabulary with major frequency or equal to 3 has a size of 500,000 words, and there is a total of 100,000 files, and as the matrices are real, the double is occupied as type of data.
It can be used the following formula to have an idea of the space in RAM to be able to execute the system (the formula gives the result in Gigabytes):
So that for this situation are necessary 4.47 Gigabytes. This formula is only as reference for the creation of these matrices, since in the parallel stages each thread occupies certain variables to perform its work, whereby it is recommended for the RAM to be at least the double of the result of
4.2.2 First Iteration
As the name of this stage indicates it, it is based on the first iteration on the corpus. To carry out the parallelization, the files spread between threads, and the matrixes
4.2.3 Iterations
This stage is perhaps the most important, the cause that the system develops in parallel, since according to the number of iterations, it is the number of times that each file has to open, that is to say, if there is a corpus with 100,000 files and it is wanted to do1000 iterations, then a total of 100,000,000 files would have to open, which is not a small quantity. Which, similarly to stage 1, in each iteration, the files are divided between all threads, so that the matrixes ntk and nkm are shared again; furthermore of k, beta, and alfa. And the actualization of both matrixes is done using Gibbs Sampling.
4.2.4 Creation of Theta
Once it is finished the part where the heaviest weight of the processes of the system is recharged, theta is calculated. At the end of the calculations, theta contains the probabilities, of each topic, of belonging to each document. In this stage, parallelization is possible spreading the rows of the matrix theta between threads.
4.2.5 Creation of Phi
Stage 5 is very similar to stage 4, with the difference that now the probabilities that each word belongs to each topic will be stored in phi. Similarly, parallelization is possible dividing the rows of phi between threads.
4.2.6 Most Representative Topics of a Document
In this point of the program, there is only interest for the words that best describe each document/file, so that in this parte the 10 topics with higher odds for each file are sought in theta. Once found they are stored in a text file.
4.2.7 Representative Words of a Topic
Similar to stage 6, in this stage the interest is to search for words that best represent the topics, so that in phi are sough for each topic the 20 words with the highest odds. Once found, they are stores in a text file.
4.2.8 Entropy Calculation
It has been added this last stage, which helps to measure the entropy of the results. This part serves to identify an optimal amount of topics, that is to say, in the beginning we may not know the exact number of topics that the corpus, nevertheless, after executing the system with different quantities of topics, a graphic can be constructed with the result of this stage, and based on the graphic, the optimal amount of topics for the corpus could be observed.
4.3 Execution of the LDA System
The corpus that was used as a base is the Wikicorpus in Spanish [23], which contains about 120 millions of words.
4.3.1 Pre-Processing of Data
This part is fundamental in the execution of this system, since it is where the input data are “cleared” so that good results are obtained. Abella and Medina [1] talk a little of the pre-processing de datos, from which stand out:
— Elimination of punctuation marks.
— Reduction of capital letters.
— Elimination of labels if it comes from a document type XML.
— Elimination of empty words; those that does not contribute with any meaning to the text. An example of these are articles, prepositions, conjunctions, etc.
— Extraction of etymons and slogans.
Preserving this pre-processing, it is found that in the state of art that the Polytechnic University of Catalonia and the Pompeu Fabra University have processed the Wikicorpus, this group has lemmatized and labeled the corpus. This corpus already lemmatized will be applied to LDA system [9].
4.3.2 Execution
The system LDA has been executed in the National Laboratory of Supercomputer of Southeast of Mexico in normal nodes [18] , where each node has 12 cores with a frequency of 2.5 GHz, besides they count with 126 Gigabytes of RAM memory.
Remembering that the system has been programmed with Lenguaje C++ and the API of OpenMP; in each parallel stage, 24 threads are created with the purpose that for each thread be executed by a different core.
5 Results and Discussion
The system LDA was executed with 300 iterations and with a variable amount of topics, ranging from 100 to 4000 topics. Results can be seen in the Table 6.
Table 6 Results of 300 iterations
| Topics | Entropy | Topics | Entropy |
| 100 | 9.11148 | 1200 | 8.63675 |
| 200 | 9.01459 | 1300 | 8.61248 |
| 300 | 8.94128 | 1400 | 8.59993 |
| 400 | 8.88203 | 1500 | 8.58606 |
| 500 | 8.83977 | 1600 | 8.57487 |
| 600 | 8.79597 | 1700 | 8.55774 |
| 700 | 8.76163 | 1800 | 8.54389 |
| 800 | 8.72798 | 1900 | 8.52989 |
| 900 | 8.70400 | 2000 | 8.51713 |
| 1000 | 8.67401 | 3000 | 8.43023 |
| 1100 | 8.66157 | 4000 | 8.36932 |
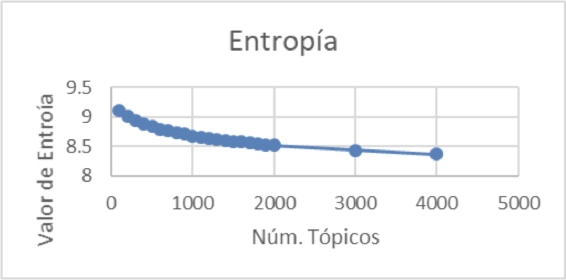
With these data, the graphic of Fig. 8 was obtained, where it can be seen a decrease and, that after 1300 topics, the entropy starts to gradually decrease. In this setting, it was chosen as amount of topics 1300.
Once chosen the value of 1,300, the system LDA has been executed again with 1,000 iterations.
Then, some topics with their words and their respective probabilities in the topic generated by system LDA for 1,300 topics with 1,000 iterations are presented in Table 7.
Table 7 1,300 topics and their probabilities
| Topic_334 | Topic_413 | Topic_418 | |||
| roberto | 0.01567 | game | 0.06414 | play | 0.02811 |
| year | 0.00948 | videogame | 0.00929 | club | 0.02808 |
| no | 0.00741 | character | 0.00728 | football | 0.02726 |
| gómez | 0.00625 | power | 0.00706 | team | 0.02686 |
| rodríguez | 0.00487 | saga | 0.00669 | selection | 0.01437 |
| all | 0.00478 | no | 0.00659 | first | 0.01362 |
| chespirito | 0.00475 | cisneros | 0.00594 | goal | 0.01352 |
| first | 0.00443 | developers | 0.00588 | division | 0.01312 |
| program | 0.00429 | also | 0.00585 | match | 0.01212 |
| city | 0.00422 | player | 0.00542 | tournament | 0.01073 |
| other | 0.00420 | all | 0.00481 | season | 0.00950 |
| iso | 0.00415 | console | 0.00478 | footballer | 0.00927 |
| jesús | 0.00399 | other | 0.00472 | player | 0.00879 |
| aramón | 0.00356 | version | 0.00472 | year | 0.00862 |
| where | 0.00343 | mode | 0.00446 | champion | 0.00799 |
| screenwriter | 0.00341 | gamecube | 0.00439 | national | 0.00785 |
| character | 0.00332 | wii | 0.00413 | dispute | 0.00743 |
| fernández | 0.00324 | protocol | 0.00382 | win | 0.00694 |
| power | 0.00315 | software | 0.00380 | debute | 0.00662 |
| mexican | 0.00309 | year | 0.00378 | championship | 0.00627 |
| club | 0.04666 | orchestra | 0.03887 | cv | 0.03641 |
| team | 0.04375 | piano | 0.03185 | motor | 0.02912 |
| play | 0.03234 | music | 0.02398 | cylinder | 0.01561 |
| season | 0.03169 | concert | 0.01781 | four | 0.01438 |
| match | 0.02597 | oeuvre | 0.01712 | automobile | 0.01204 |
| football | 0.02417 | violin | 0.01525 | line | 0.01057 |
| link | 0.02372 | composer | 0.01511 | generation | 0.00983 |
| cup | 0.01963 | op | 0.01448 | year | 0.00857 |
| selection | 0.01558 | guitar | 0.012823 | external | 0.00748 |
| division | 0.01502 | musical | 0.01169 | game | 0.00706 |
| goal | 0.014972 | symphonic | 0.01065 | five | 0.00694 |
| player | 0.01456 | composition | 0.00993 | first | 0.00692 |
| dispute | 0.01235 | director | 0.00928 | bodywork | 0.00666 |
| champion | 0.011898 | opus | 0.00818 | traction | 0.00653 |
| first | 0.01004 | pianist | 0.00805 | version | 0.00642 |
| football | 0.00900 | musician | 0.00740 | gasoline | 0.00641 |
| spanish | 0.00881 | major | 0.00639 | power | 0.00598 |
| athletic | 0.00850 | year | 0.00563 | diesel | 0.00581 |
| final | 0.00824 | piece | 0.00535 | injection | 0.00540 |
| trainer | 0.00761 | sonata | 0.00514 | maximum | 0.00512 |
| patient | 0.03165 | candidate | 0.03174 | island | 0.04056 |
| disease | 0.02630 | election | 0.02674 | tropical | 0.03674 |
| symptom | 0.01986 | vote | 0.02366 | hurricane | 0.02882 |
| disorder | 0.01595 | party | 0.01459 | storm | 0.02735 |
| doctor | 0.01256 | political | 0.00764 | atlantic | 0.01935 |
| power | 0.01105 | coalition | 0.00734 | wind | 0.01643 |
| pain | 0.00952 | candidacy | 0.00671 | ice | 0.01511 |
| no | 0.00927 | electoral | 0.00668 | coast | 0.01461 |
| other | 0.00706 | obtain | 0.00666 | ocean | 0.01368 |
| medicament | 0.00632 | seat | 0.00619 | soil | 0.01147 |
| affect | 0.00556 | no | 0.00592 | km | 0.01125 |
| mental | 0.00513 | method | 0.00527 | north | 0.01033 |
| effect | 0.00443 | choose | 0.00520 | season | 0.00928 |
| medicine | 0.00418 | jaime | 0.00467 | rain | 0.00862 |
| studio | 0.00405 | deputy | 0.00438 | damage | 0.00772 |
| duty | 0.00396 | all | 0.00424 | west | 0.00762 |
| nervous | 0.00388 | year | 0.00422 | cause | 0.00740 |
| thumb | 0.00383 | result | 0.00417 | sea | 0.00735 |
| produce | 0.00381 | other | 0.00403 | south | 0.00730 |
| also | 0.00381 | power | 0.00371 | cyclone | 0.00729 |
It must be highlighted that the words that best describe a topic are those with the highest probabilities, which are ordered in descending form.
6 Conclusions and Future Work
As it can be seen in topics, good results have been found, of course there are words that do not belong to the topic, various topics are right and are easily linked to specific topics.
Getting these topics is important, for example, when it is desirable to know what does a file talk about. In this point, it is not only necessary to see the topics which it is linked, and in this way it is possible to abstract the idea of the content of the file without completely reading it.
On the other hand, not all 1,300 topics represent different themes, also to find similar topics is viable, as well as topics that contain words of several topics, which hinders to associate these topics to some specific theme. LDA is one of the algorithms more used on the field of Topic Modeling that is based, as it has been described in this work, in the concept of latent structure of topics within a great collection of documents. The method of this Gibbs sampling is the algorithm more used within the family of sampling methods. However, there are other type of algorithms that could be applied in future works, and that do not approximate a posteriori distribution with samples, but that are of deterministic type such as Variational Bayesian Inference (VB), Expectation Propagation (EP), Variational EM, inter alia, that could be implemented to compare results.











 nueva página del texto (beta)
nueva página del texto (beta)