Introducción
La regeneración de una población forestal coetánea se puede realizar de manera natural o a través de una plantación (Nyland et al., 2016). En México, para lograr la regeneración natural, es común utilizar el método de árboles padre, considerando la tolerancia y las características de las especies, usualmente sometidas a un régimen de manejo coetáneo (Musálem et al., 1994).
Hasta 2019, cerca de 35% de los planes de manejo forestal autorizados utilizaban este método de regeneración naturalaa; incluso, sistemas de manejo como el de Desarrollo Silvícola, recomiendan este método (Secretaría de Medio Ambiente Recursos Naturales y Pesca [Semarnap], 1994) con la sugerencia de dejar hasta 25 árboles por hectárea en pie.
Algunos autores han demostrado que la aplicación del método de árboles padre permite generar una regeneración exitosa en varias especies (Chacón et al., 1998; Hernández et al., 2019). Sin embargo, la estimación del número de árboles padre que asegure un adecuado cubrimiento de semilla en el sitio ha sido un problema tradicional de silvicultura y sigue siendo controversial, sobre todo porque la decisión debe considerar las características de la regeneración producida en términos de calidad y vigor, y los costos asociados a su establecimiento, como el costo de oportunidad de dejar a los árboles padre en pie y el costo de la corta de liberación (Puettman et al., 2015).
La definición del número óptimo de árboles padre depende de la interacción de múltiples factores (Nyland et al., 2016). Varios autores clásicos (Assmann, 1970; Hawley y Smith, 1972; Daniel et al., 1979; Oliver y Larson, 1990; Smith et al., 1997; Ashton y Kelty, 2018) han identificado tres grupos de factores que determinan la cantidad de árboles a dejar en pie: factores intrínsecos de la especie (altura del árbol, cobertura de copa, peso, tamaño y forma y viabilidad de la semilla, entre otros), del sitio (calidad de sitio, fisiografía) y del entorno ambiental (depredadores, vientos, clima, etc.) (Smith, et al., 1997; Nyland et al., 2016).
La interacción de todos estos factores hace que la estimación empírica del número óptimo de árboles padre por sitio y por especie enfrente un problema de dimensionalidad en el número de alternativas a evaluar. De aquí que las recomendaciones genéricas son variadas; por ejemplo, considerando el diámetro normal, se recomiendan hasta 74 árboles por hectárea con diámetros de 25 cm para Pinus taeda L. y Pinus elliottii Engelm, mientras que para rodales con diámetros de 40 cm se recomiendan 25 árboles (Barnett y Baker, 1991).
Para especies con semilla pequeña como Pseudotsuga menziesii Doug., se recomienda de 15 a 20 árboles por hectárea. Sin embargo, la densidad de árboles padre puede bajar incluso a siete árboles por hectárea en especies como Larix occidentalis Nutt., cuya semilla cuenta con una alta capacidad de dispersión al ser pequeña y ligera (Schmidt et al., 1976). El problema de dimensionalidad dificulta la realización de un número tal de experimentos que cubran todas las condiciones y sus interacciones, por lo que los resultados obtenidos de las evaluaciones sobre la eficiencia del método solo han sido aplicados al área de influencia de los experimentos, limitando su extrapolación a las áreas operativas (Barnett y Baker, 1991).
En contraste, la regeneración a través de plantación tiene un costo mayor, dado que requiere inversión en planta, así como en el establecimiento de la plantación (Dlugosiewicz, Zając y Wysocka-Fijore, 2019; Dlugosiewicz, Zając, Wysocka-Fijore y Sułkowska, 2019). Esta inversión generalmente representa una restricción al momento en que los productores toman la decisión entre regenerar o no, artificialmente. Por lo anterior, la decisión resulta altamente sensible a la magnitud de los costos de reforestación, a la disponibilidad de apoyo gubernamental, a la asistencia técnica existente y a la disponibilidad de insumos para la reforestación (Royer, 1987). Adicionalmente, cuando se trata de regeneración asistida, es necesario tener control de la calidad de planta que se utiliza, la cual debe provenir de colectas de semilla en árboles de la zona a regenerar con características fenotípicas deseables (Ashton y Kelty, 2018). A pesar de ello, la plantación puede tener ventajas económicas, como el aprovechamiento de los árboles padre al momento de la corta de regeneración, que se refleja, en una ganancia inmediata y un menor costo futuro de extracción, así como en una reducción de los costos asociados al posible daño a la regeneración al momento de realizar la corta de liberación (Barnett y Baker, 1991; Stokes et al., 2020).
Lo anterior sugiere que la plantación podría ser más deseable que la regeneración natural en algunas circunstancias, ello sin considerar las probables ventajas técnicas vinculadas a una ganancia en el tiempo de establecimiento, mejora de las características genéticas y una ganancia de vigor de la planta establecida, entre otras (Rums et al., 2020). Cabe señalar que, en sitios con buena productividad, la regeneración natural podría producir poblaciones de mayor vigor y crecimiento que una plantación (Falfán-Cortés et al., 2021).
Estas ventajas y desventajas de ambos métodos de regeneración (plantación o natural) hacen evidente la necesidad de evaluar, bajo una amplia gama de condiciones, la rentabilidad de regenerar a través de una plantación en comparación con la regeneración natural, bajo el supuesto de que la primera podría tener al menos las mismas ventajas desde el punto de vista técnico que la regeneración natural.
Objetivos
El objetivo de este trabajo fue evaluar la rentabilidad del método de regeneración natural a través del sistema silvícola de árboles padre respecto a la regeneración por plantación, bajo una amplia gama de condiciones de sitio y económicas, usando un modelo de simulación.
Materiales y métodos
El procedimiento para contrastar los costos de una regeneración natural contra una plantación se llevó a cabo en cuatro etapas: 1) Desarrollo de un algoritmo para estimar el número de árboles padre con base en atributos del sitio y de la población; 2) Calibración (identificación de valores idóneos para los parámetros del modelo) del algoritmo con base en información disponible; 3) Definición de la estructura de costos y beneficios de ambos procedimientos de regeneración a lo largo de un periodo de regeneración; y 4) Estimación de la rentabilidad de diferentes condiciones de sitio y económicas de ambos métodos de regeneración y la generación de una distribución de probabilidades empírica de las diferencias en utilidades de ambos métodos.
Desarrollo del algoritmo de estimación del número de árboles padre
Se idealizó un rodal cuadrado de una hectárea de superficie (100 m × 100 m) con una distribución regular de N árboles padre a dejar en pie en la superficie de interés. N es el mínimo número de árboles padre requeridos de acuerdo con las características de cada especie para una condición de sitio particular. Se consideró que la distribución de los N árboles en la superficie fue:
donde:
A = número de árboles distribuidos en los 100 m de longitud de cada lado del cuadrado considerado (Fig. 1)
Para definir el valor de A, se tomó en cuenta que está inversamente relacionado con la altura, dado que a mayor altura mayor área de dispersión de semillas. También se consideró que la altura a una edad reproductiva depende en gran medida de la calidad de sitio, misma que se puede aproximar por el índice de sitio (IS) y que, a su vez, IS se define como una altura estandarizada dada una calidad de sitio. De acuerdo con las consideraciones anteriores, se aproximó A como:
Donde:
IS = índice de sitio
A = número de árboles en el lado del cuadrado idealizado
La ecuación 2 estima el número de árboles padre en 100 m, separados por una distancia igual al IS. No obstante, este modelo no considera que, a medida que incrementa la altura, la cantidad de semilla dispersada tiene incrementos marginales decrecientes hasta, quizá, alcanzar un valor asintótico máximo de distancia de dispersión de semilla de un solo árbol. Esta consideración se añadió al modelo incorporando un exponente, α, al índice de sitio (Ecuación 3) con la restricción de que solo tome valores en el intervalo (0, 1). Este exponente permite incorporar el efecto del entorno ambiental (vientos, pendiente, fisiografía, entre otros) en la estimación del número de árboles padre. Un valor muy pequeño implicaría que el incremento en la altura del arbolado tiene poco efecto en asegurar una adecuada dispersión de la semilla; por el contrario, valores de α cercanos a la unidad identificarían especies y situaciones de sitio donde la altura del arbolado tiene un fuerte efecto en asegurar una adecuada dispersión de semilla.
donde:
α = parámetro del modelo
El modelo se puede afinar aún más, al incluir un parámetro que incorpore el efecto de los agentes de disturbio y factores intrínsecos de la especie, mismos que podrían obligar al silvicultor a dejar un número mínimo de árboles padre conforme a la especie y el entorno ambiental. Ejemplos de ello pueden ser la cantidad de roedores, como ardillas, o plagas que puedan reducir la cantidad de semilla disponible para regeneración (Velázquez-Martínez y Musálem, 1986; Nuñez et al., 2008; Steele y Yi, 2020). El efecto de estos agentes y factores puede considerarse añadiendo un parámetro más como se muestra en la ecuación 4:
donde:
β = Factor de ajuste para considerar el número mínimo de árboles a dejar en pie en una condición de sitio dada
Un valor grande de β resulta en un menor número de árboles padre, lo que reflejaría un limitado efecto negativo de la condición de sitio sobre N De esta forma, el algoritmo para calcular el número de árboles padre se traduce en:
Calibración de parámetros
La calibración del modelo (5) se puede realizar por un ajuste de regresión en el caso de contar con varias observaciones (caso poco común), o bien aproximando los parámetros α y β a partir de un par de observaciones. Para ejemplificar este segundo caso se idealizó un rodal con índice de sitio para la especie X de 10 m (10 m a la edad de 50 años). En estas condiciones de sitio, las recomendaciones sobre densidad de árboles padre señalan que N = 30 árboles por hectárea garantizan que la especie X se regenera naturalmente en forma apropiada dentro del periodo de regeneración recomendado. Dado que no se cuenta más que con un par de referencias sobre la densidad reomendada de árboles padre, se hipotetiza un valor de α por ejemplo α =0.25. Con esta información y utilizando la ecuación (5) se aproxima el factor de ajuste β con la siguiente expresión:
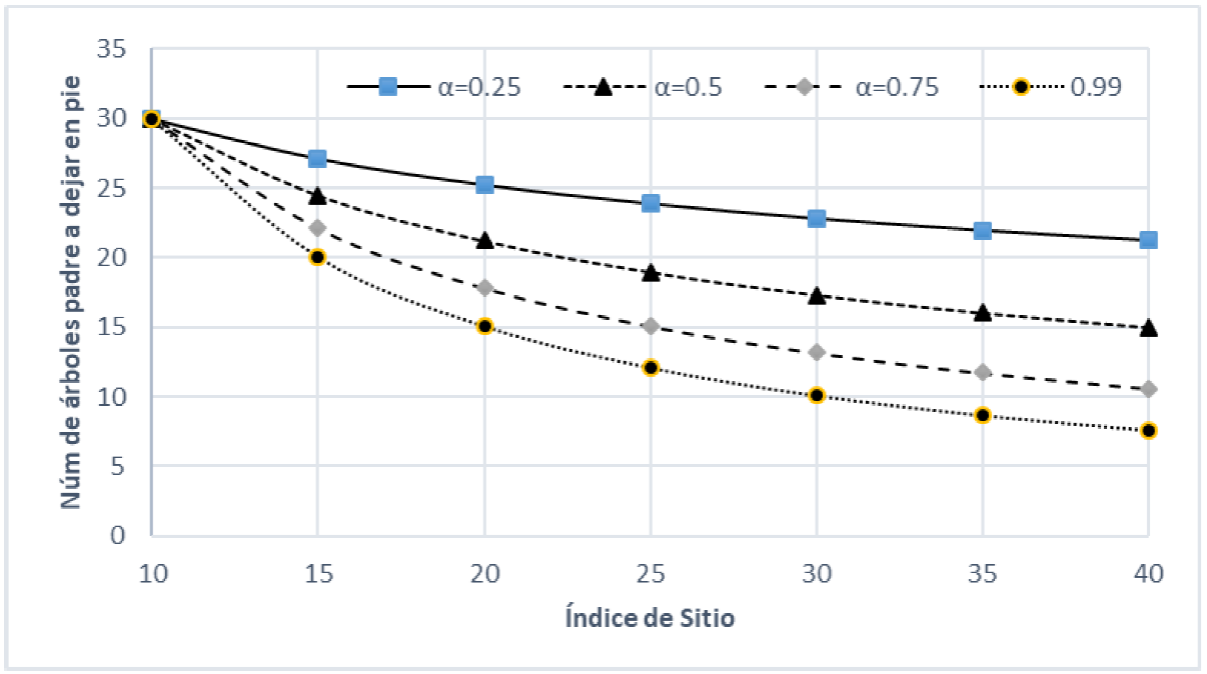
De esta forma, dado el valor de β estimado con la ecuación 6, se puede calcular el número mínimo de árboles padre para el IS=10 y α =0.25. La Figura 2 muestra varias trayectorias del número de árboles padre para diferentes valores de α e IS. El modelo 5 permite cambiar la forma y la escala de la tendencia, de aquí que la calibración requerirá que la selección de los valores de α y β sea tal que la trayectoria de N se aproxime a los valores de N que señalan las recomendaciones disponibles de densidad de árboles padre.
Estructura de costos y beneficios entre sistemas de regeneración
Los costos considerados para estimar el costo de regeneración natural fueron: el costo de oportunidad del valor de la cosecha durante el periodo de regeneración y el costo de un mantenimiento adicional de la infraestructura para realizar la extracción durante la liberación (m). El valor de la cosecha dejada en pie expresado como función de N se aproximó de la siguiente forma:
donde:
VC = valor de la cosecha dejada en pie (MXN ha-1)
p = precio por metro cúbico del volumen comercial en pie (MXN m-3)
k = factor de corrección (m3 m-1) que transforma la altura definida por el índice de sitio (IS) en volumen comercial
N = número árboles padre a dejar en pie
α y β = parámetros del modelo
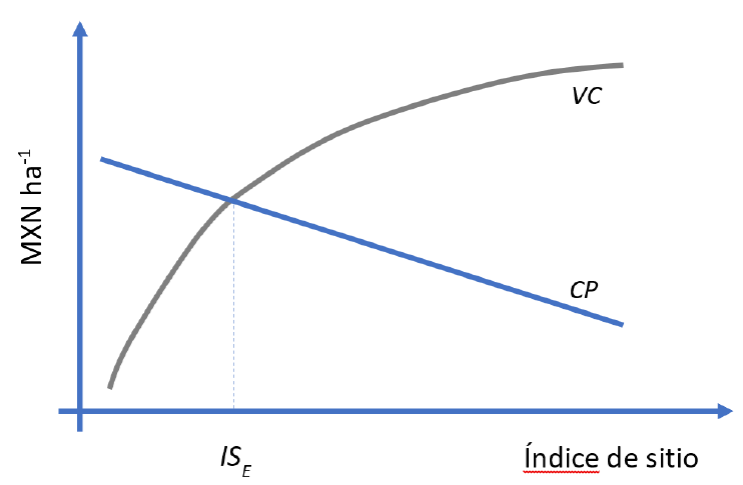
La ecuación 7 muestra que VC aumenta con el precio y con el volumen (aproximado por k (IS)) y se reduce con β y α. Aún más, dada una β fija (número mínimo N), VC ≅ Kp (IS) 1-α (considerando un cambio de variable K = k / β). Es importante notar que, a pesar de que N se reduce al aumentar IS, el VC aumenta con el IS en tanto α < 1 y cercano a cero, tal y como se esperaría (Fig. 3). El costo de mantenimiento (m) se asume único al momento de la corta de liberación.
Por su parte, el costo de plantación (CP) está compuesto por un costo fijo (c), más un costo variable (b), definido por las características del sitio, mismas que también se pueden aproximar por el índice de sitio. El costo fijo incluye componentes como el costo de la planta (bajo el supuesto de una densidad de plantación constantes) y el mantenimiento inicial de la plantación, mientras que en el componente de costo variable se incluyen el costo de preparación de sitio, el transporte de brinzales y el plantado, los cuales están relacionados con el IS.
Regularmente, el costo variable es menor en la medida que el sitio tiene mejores características, por lo cual este costo es inversamente proporcional al IS, lo cual se puede aproximar por b (IS), donde b es un escalar negativo. Por tanto, el CP se expresa como:
donde:
CP = costo de plantación (MXN ha-1)
b = costo variable de plantación (MXN ha-1)
c = costo fijo de plantación (MXN ha-1)
Bajo los supuestos de este modelo, la trayectoria del CP como función del IS es una línea con pendiente negativa (Fig. 3). Es importante notar que las trayectorias de CP y VC muestran que debe existir una calidad de sitio, IS E , tal que para mejores condiciones de sitio no resulta económico dejar arbolado en pie y debe optarse por la regeneración asistida.
La Figura 4 muestra una línea de tiempo para el año t 0 , momento en que se cosecha todo el arbolado para el caso de la plantación, o bien la cosecha obtenida por la corta de regeneración con el método de árboles padre. La línea de tiempo también muestra el año t, momento en que se hace la corta de liberación para el caso de la regeneración por árboles padre. Para el caso de la plantación, la ganancia considera el valor de la cosecha total de los árboles padre y el costo corresponde al CP. De esta forma, la utilidad neta derivada de la plantación (π p ) en t 0 corresponde al valor de la cosecha de los árboles padre. (VC) menos el costo de ésta (CP); esto es, π p = VC - CP.
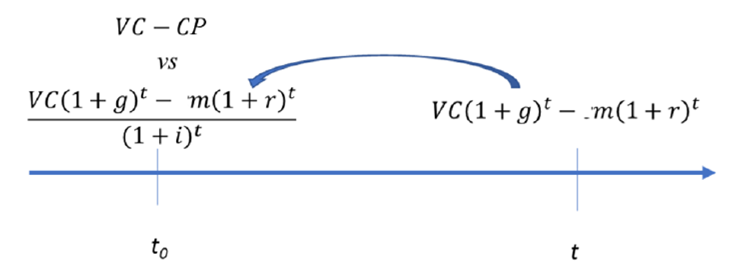
Figura 4 Línea de tiempo donde se verifican las ganancias de la regeneración asistida vs la regeneración por árboles padre.
En contraste, la regeneración por árboles padre implica que no se realiza inversión alguna en el año t 0 , mientras que los beneficios de la cosecha de los árboles padre se obtienen hasta el año t, año en que se realiza la corta de liberación. Para poder comparar ganancias de la plantación vs el método de árboles padre se han hecho las siguientes consideraciones: 1) los árboles padres tendrán un crecimiento adicional y el valor de la cosecha deberá aumentar, aunque sea marginalmente; 2) en el año t existirá un costo adicional por mantenimiento de caminos (m), que será más alto a medida que la regeneración toma más tiempo; 3) estos cambios suceden en el año t, por lo que para comparase con las ganancias de la regeneración asistida deben actualizarse al año t 0 calculando su valor presente neto. La inclusión de estas consideraciones asume que el crecimiento adicional se puede expresar como un crecimiento anual porcentual, g sobre el valor de la cosecha. Este valor es regularmente muy pequeño (0%-4%) debido a que los árboles padre son arbolado maduro que regularmente muestra un crecimiento reducido. Como referencia se puede citar que, en especies de rápido crecimiento e índices de sitio de buena calidad, el crecimiento porcentual puede alcanzar un promedio de 6% hacia la edad del turno (Peters y Jarpa, 1982).
Para el costo adicional por mantenimiento (m) se presume un aumento anual con una tasa r. Por tanto, el valor presente neto de la utilidad neta derivada de la cosecha de los árboles padre (π AP) en el año t se puede expresar como:
donde:
m = costo de mantenimiento de vías de saca (MXN ha -1)
R = tasa de aumento en el costo de mantenimiento posterior a la corta de regeneración (MXN ha -1 año-1)
i = tasa de descuento usada para convertir el valor futuro a un valor presentebb
La tasa de descuento i se puede aproximar con una tasa de interés bancario o bien a través de una tasa social de descuento (Edwards, 2016).
Comparación de la utilidad neta de los sistemas de regeneración
La comparación de la utilidad neta derivada de la regeneración natural (π AP ) con aquella de la plantación (π P ) se realizó con una simulación Monte Carlo con 20 000 pruebas; la variable de respuesta de la simulación fue la diferencia entre utilidades netas (D) de la plantación respecto de la regeneración natural, esto es:
donde:
πAP= beneficio neto derivado de la regeneración natural (MXN ha-1)
πP = beneficio neto derivado de la plantación (MXN ha-1)
La simulación se realizó variando todos los parámetros que se han identificado en la estructura de costos y el modelo de número de árboles padre, considerando un periodo de regeneración t. Para cada parámetro del modelo se definió una distribución de probabilidades uniforme dentro de un intervalo de valor máximo y mínimo (Tabla 1). A partir de esta simulación se construyó una distribución de frecuencias relativas para la diferencia entre utilidades netas (D), dado un periodo de regeneración t. Ello permitió estimar la probabilidad de que las utilidades de uno método de regeneración puedan ser mayores que las de otro para cada periodo de regeneración considerado.
Tabla 1 Valores mínimos y máximos usados para la simulación Monte Carlo de la diferencia del valor presente de las ganancias de la plantación vs la regeneración por árboles padre.
| Parámetro | Distribución | Valor mínimo | Valor máximo | Unidad |
| β | Uniforme | 80 | 120 | factor |
| α | Uniforme | 0.3 | 0.6 | factor |
| IS (Indice de Sitio) | Uniforme | 15 | 30 | metros |
| p (Precio del volumen en Pie) | Uniforme | 1100 | 1300 | MXN (2022) |
| k (fator de conversión altura-volumen en pie) | Uniforme | 0.1 | 0.25 | factor |
| b (costo variable de reforestación) | Uniforme | -120.00 | -340.00 | MXN (2022) |
| i (tasa de descuento) | Uniforme | 0.05 | 0.15 | factor |
| r (tasa de aumento costo de rehabilitación) | Uniforme | 0.02 | 0.04 | factor |
| m (Costo de rehabilitación de vías de extracción) | Uniforme | 12 000.00 | 23 500.00 | MXN (2022) |
| c (Costo fijo de reforestación) | Uniforme | 22 000.00 | 43 500.00 | MXN (2022) |
| g (tasa anual de crecimiento del arbolado en pie) | Uniforme | 0.01 | 0.04 | factor |
Cabe señalar que la variación del periodo de regeneración t se consideró realizando las 20 000 pruebas para cada periodo de regeneración asumido. La simulación se realizó con la aplicación RISK-SIMULATOR (Real Option Valuation [ROV], 2019).
Resultados
Los resultados de cada simulación permitieron construir una distribución empírica de frecuencias para la variable (D), en cada periodo de regeneración (t) evaluado. La Figura 5 muestra la distribución empírica de frecuencias de la variable D para un periodo de regeneración, t = 6. La distribución resultante es una distribución con asimetría negativa (coeficiente de asimetría = -0.9) que muestra la alta probabilidad de tener valores muy pequeños para D (diferencia entre el valor presente neto de la ganancia neta de la regeneración natural menos la ganancia neta de la plantación), que se traducen en utilidades netas de la plantación mayores que aquellas obtenidas con la regeneración por árboles padre. La línea roja mostrada en la distribución empírica (Fig. 5) muestra el parteaguas entre valores positivos y negativos de D; valores negativos reflejan π AP < π P , por lo que la plantación es más deseable desde el punto de vista económico.
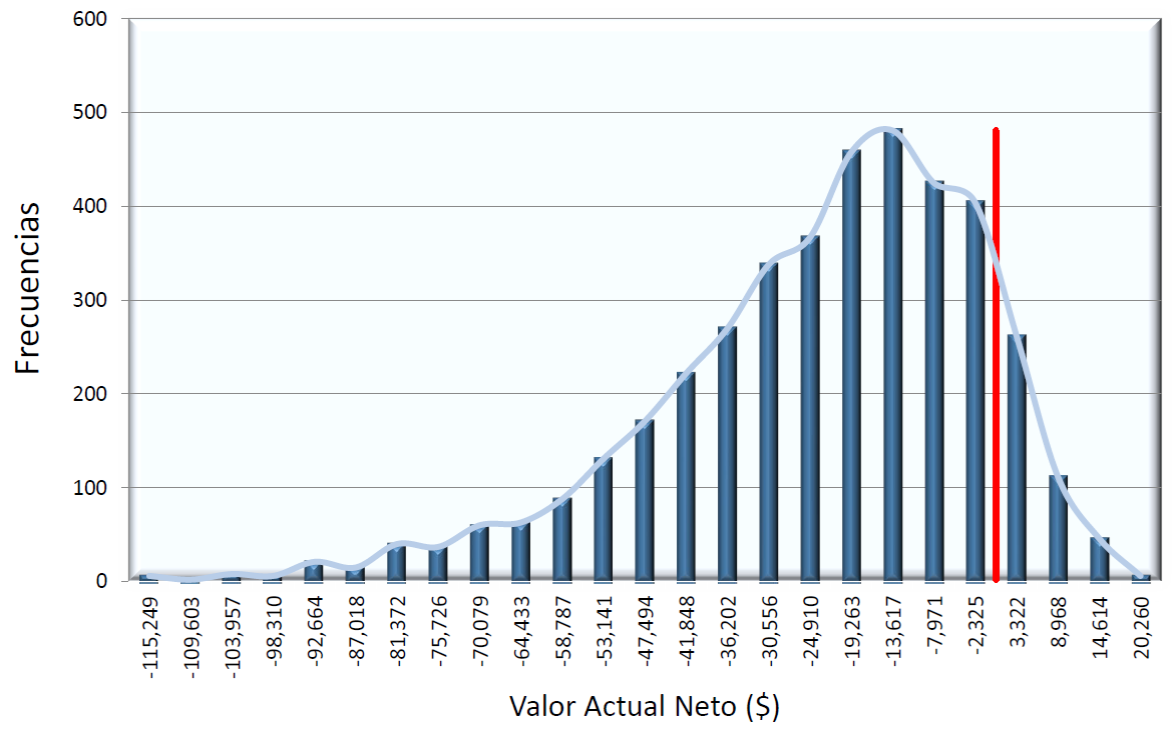
La línea roja representa un VPN = 0.
Figura 5 Distribución de frecuencias del valor presente neto (VPN) de la diferencia de beneficios entre la regeneración natural y la plantación (t = 6) considerando 20 000 simulaciones.
La asimetría de las distribuciones obtenidas para cada periodo, t, varió muy poco. Las distribuciones de D fueron marginalmente más simétricas para periodos de regeneración cortos que para periodos de regeneración largos. Adicionalmente se observó que las distribuciones para periodos de regeneración largos tuvieron mayor variación (desviación estándar) que las distribuciones para los periodos cortos. Ambos resultados muy probablemente están vinculados al mayor efecto de las tasas de descuento grandes que pudieron haberse seleccionado de manera aleatoria, lo que a su vez se asocia al mayor riesgo (costo) vinculado a periodos de regeneración largos.
La Tabla 2 resume dos indicadores de interés obtenidos a partir de la distribución de probabilidad para cada periodo de regeneración simulado: promedio de la variable D y probabilidad de que esta diferencia sea menor o igual a cero, estimación realizada con base en la distribución empírica de la variable D obtenida por simulación (Fig. 5). Ambos atributos muestran claramente que, bajo una amplia gama de condiciones de sitio y de supuestos de regeneración, la rentabilidad económica de la regeneración asistida es superior a la regeneración natural para periodos de regeneración superiores a dos años, dado que D < 0 con una probabilidad superior a 54% y, como se esperaría, aumenta a medida que el periodo de regeneración se alarga. El resultado sugiere que, si no existen limitantes ecológicas, de sitio y de especie (tolerancia), es recomendable, desde el punto de vista económico, realizar una plantación para regenerar una población (rodal) a la que se la haya aplicado una corta de regeneración.
Tabla 2 Indicadores de D (diferencia entre el valor presente neto de la ganancia neta de la regeneración natural menos la ganancia neta de la plantación) para diferentes periodos de regeneración.
| Periodo de regeneración (años) | Diferencia promedio (MXN 2022) | Probabilidad de que la diferencia sea menor que cero (%) |
| 1 | 8460.31 | 13 |
| 2 | 2753.81 | 36 |
| 3 | -2513.12 | 54 |
| 4 | -7367.60 | 66 |
| 5 | -11 855.96 | 75 |
| 6 | -16 003.06 | 81 |
| 7 | -19 838.28 | 85 |
| 8 | -23 387.61 | 88 |
| 9 | -26 674.78 | 91 |
| 10 | -29 721.26 | 92 |
Discusión
El modelo de estimación del número de árboles padre asume que la estimación con base en el índice de sitio y los parámetros del modelo aseguraría una producción de semillas en cantidad y calidad que permitirán una regeneración adecuada. Sin embargo, lograr este objetivo requiere una calibración más precisa para cada especie y condición de sitio. Esto es posible de lograr con información de inventarios poscosecha y el uso de algoritmos de imputación de estimaciones de regeneración como el documentado por Ek et al. (1996) o procesos de simulación con información parcial (Ribbens et al., 1994). El algoritmo aquí presentado difiere de las metodologías tradicionales de predicción de regeneración natural a partir de modelos regresión que proyectan la incorporación con base en calidad de sitio y algunas otras características del rodal (Solomon, 2002). Estos modelos son muy dependientes de la calidad de datos y carecen de una estructura que permita estimaciones robustas (Bravo et al., 2019) y que pueda evolucionar a una estimación con base en procesos.
En este contexto, el único algoritmo estructural o modelo basado en procesos para estimar regeneración natural posterior a una corta de regeneración (bajo tratamientos de cortas sucesivas o protección) parecido al algoritmo aquí propuesto es el desarrollado por Merganič y Fabrika (2011). Este último algoritmo es más sofisticado que el de este estudio, pues asocia variables climáticas, de sitio y del rodal (diámetro cuadrático promedio y la densidad relativa del rodal) a la producción de semillas viables y su calibración se realiza a través de datos de inventario poscosecha. Ello muestra que existe una ventana de oportunidad para mejorar el algoritmo aquí propuesto para incluir variables adicionales que permitan mejorar la estimación del número de árboles padre y de las características de la regeneración producida con base en el número de árboles padre proyectado, como los principios y modelos propuestos por Nathan y Muller-Landau (2000) o con el uso de modelos determinísticos (Hernández-Rivera et al., 2020) o probabilísticos (Nathan et al., 2002). Refinamientos de este tipo podrían generar recomendaciones más precisas sobre la densidad de árboles padre para regenerar apropiadamente un área, tema de sumo interés sobre todo en regiones tropicales (Holl, 1999). Estos refinamientos sin duda proporcionarán recomendaciones puntuales por sitio, especie y condición de mercado. Sin embargo, la evaluación de la utilidad neta de uno y otro método de regeneración a través de experimentos de campo requiere de un tamaño de muestra muy grande para incluir todo el conjunto de variantes de especie, sitio y variables económicas que determinan la aplicación de cada método. Por ello, la simulación, con base en un modelo fiable es una aproximación robusta para estimar la probabilidad de ocurrencia de un resultado que es determinado por un número muy grande de variables.
El principal resultado de este estudio muestra que, desde el punto de vista económico y bajo una amplia gama de condiciones de sitio y especie (variables del modelo), es más rentable realizar una plantación que regenerar al rodal con el método de árboles padre. La mayor rentabilidad de la primera es atribuible fundamentalmente a la depreciación del valor del arbolado dejado en pie a lo largo del periodo de regeneración y los mayores costos de posponer la cosecha. Sin embargo, el resultado no considera que hay variables que tienen un gran peso en la toma de decisiones del productor como: apoyos del estado, condiciones de mercado, atributos del propio productor (edad, ingreso, conocimiento técnico, objetivos de manejo de su predio) y características de la propiedad. Estas últimas pueden ser muy relevantes ya que algunos autores han señalado que, en condiciones de buena calidad de sitio, la regeneración natural puede ser mejor opción que la plantación (Dlugosiewicz, Zając y Wysocka-Fijore, 2019; Dlugosiewicz, Zając, Wysocka-Fijore y Sułkowska, 2019; Falfán-Cortés et al., 2021), bajo tasas de descuento moderadas (Chudy et al., 2022).
Varios estudios han mostrado que la disponibilidad de apoyos gubernamentales y asistencia técnica se encuentra consistentemente relacionada con la aplicación de una regeneración asistida o plantación (Kilgore et al., 2007). Si bien el efecto positivo de los apoyos gubernamentales en inducir la plantación es variable a lo largo del tiempo y depende de múltiples factores de mercado, sitio y características de los productores (Sun, 2007), es innegable que la disponibilidad de apoyos para plantar un área cosechada inducen a que más productores participen en este tipo de actividades, sobre todo si están acompañados de asesoría (Ovaskainen et al., 2017) y organización para la producción de insumos de reforestación como viveros y uso compartido de maquinaria y equipo (Sun, 2007). Además, otros autores han demostrado que estos apoyos tienen efectos multiplicativos, en tanto inducen a los productores vecinos a adoptar estrategias de manejo más intensivas en términos de rendimiento maderable y rentabilidad (Jones et al., 2010), lo que genera un círculo virtuoso de mejora en los sistemas de producción y bienestar para los propietarios del bosque.
En relación con el efecto de las variables de mercado que inducen la selección de una regeneración asistida por parte de los productores, otros autores han documentado que variables como: mejores precios de la madera, bajas tasas de interés a corto plazo (Sun, 2007) y un valor alto de la tierra favorecen la elección de una plantación (Beach et al., 2005). Dentro de las variables de la propiedad que mayormente influyen en la decisión a favor de esta están la calidad del sitio (Zhang y Pearse, 1997), las especies comerciales dentro de la propiedad y la estructura de costos de plantación definida por la calidad de la tierra (Ovaskainen et al., 2006). Finalmente, en el otro extremo del espectro, también se ha documentado que algunos atributos del productor, como su nivel de ingreso y diversidad de actividades económicas influyen para que este opte por realizar la plantación (Beach et al., 2005).
Lo anterior sugiere que, a pesar de que la plantación parece una estrategia técnica y económicamente más atractiva que la regeneración natural, los productores podrían estar lejos de adoptarla si no concurre un conjunto de factores de política pública, mercado, condición del sitio y perfil del productor que incentiven su aplicación. Tales factores podrían fomentarse a través de la dotación de incentivos directos o en especie, la disponibilidad de asistencia técnica especializada, así como el desarrollo de mercados de productos y servicios intermedios (producción de planta, renta de maquinaria/equipo de reforestación, fomento de un mercado laboral capacitado), entre otros.
Finalmente, es importante señalar que la plantación no solo resultará en una mejora en el nivel de producción y bienestar del propietario, sino que promoverá el desarrollo de otras actividades productivas (producción de semilla y planta de calidad y provisión de bienes y servicios para plantación) generadoras de círculos virtuosos de producción y bienestar local, sin olvidar los beneficios vinculados al aumento de productividad de los sistemas forestales y el incremento de los incentivos para conservarlos. De aquí que la inversión en estrategias de apoyo directo o en especie dirigidas a promover la regeneración por plantación (cuando es factible técnicamente) en bosque manejados conlleva un triple propósito: mejora productiva, mejora de bienestar local y eficiencia económica.
Conclusiones
A diferencia de lo que usualmente se especula, la plantación es una opción económicamente más factible que la regeneración natural con periodos de regeneración cortos (menores a tres años) y bajo una amplia variedad de condiciones de sitio y características de especie, las cuales fueron modeladas a partir de un algoritmo basado en el índice de sitio y una extensa simulación de condiciones de sitio y mercado. La probabilidad asociada a favor de la plantación es de, al menos, 54% y este valor aumenta a medida que se alarga el periodo de regeneración. Además de las ventajas técnicas que podrían vincularse a la plantación y el potencial aumento en la productividad forestal de largo plazo derivado de su aplicación, esta actividad promueve el desarrollo de otras actividades productivas (producción de bienes y servicios vinculados al establecimiento de plantaciones) que mejoran el bienestar de los productores y detonan el desarrollo local en beneficio de una población más grande.











 nueva página del texto (beta)
nueva página del texto (beta)