Introducción
La relación que existe entre diversos factores (económicos, ecológicos, culturales, entre otros) sobre el crecimiento y desarrollo de los bosques tienden a incidir de forma directa en la productividad del sitio; la misma que se puede explicar mediante la modelación matemática y estadística enfocada al sector forestal (Ahmadi y Alavi, 2016; Guzmán-Santiago, Aguirre-Calderón y Vargas-Larreta, 2020; Quiñonez-Barraza, Zhao, Santos-Posadas y Corral-Rivas, 2020), que brindan conocimiento sobre la producción y crecimiento de los árboles (Weiskittel, Hann, Kershaw y Vanclay, 2011).
La calidad de sitio estimada a partir de la productividad es un referente en el manejo forestal para la toma de decisiones, también lo es la selección de especies a cultivar para obtener un alto rendimiento en la cosecha de la masa forestal (Vargas-Larreta, Álvarez-González, Corral-Rivas y Aguirre Calderón, 2010; Baluarte-Vásquez y Álvarez-Gonzales, 2015; Sharma y Parton, 2018). Diéguez-Aranda et al. (2009) afirman que, en áreas de alta calidad de estación, la mayoría de las especies producen alto volumen maderable. Este alto potencial de incremento indica que el patrón de crecimiento en altura de los árboles con buen grosor o clases sociológicas (árboles dominantes y codominantes) está poco afectado por la densidad del rodal y de las distintas labores silviculturales (Clutter, Fortson, Pienaar, Brister y Bailey, 1983).
Los estudios de crecimiento en altura dominante en diversos rodales de México se remontan hasta la década de 1980 (Vargas-Larreta et al., 2017) y, a pesar de que es uno de los temas más estudiados, aún sigue siendo de interés dado que existe una gran mezcla de especies creciendo en distintas condiciones de productividad (Quiñonez-Barraza et al., 2015).
La productividad forestal se basa en el principio biológico y puede representar la calidad de sitio mediante un valor (índice de sitio) cuantitativo (Attis Beltrán, Chauchard y Martínez-Pastur, 2015; Hernández-Cuevas, Santiago-García, Santos-Posadas, Martínez-Antúnez y Ruiz-Aquino, 2018), donde el suelo y el clima juegan un papel importante al estar directamente relacionados (Antón-Fernández, Mola-Yudego, Dalsgaard y Astrup, 2016), a la vez estos factores ambientales están en constante cambio (Yue, Mäkinen, Klädtke y Kohnle, 2014).
El índice de sitio (IS) es el valor de la altura dominante a una edad de referencia (Mora, Meza, Porras, Sandí y Aguilar, 2019; Castillo-López et al., 2013), que puede incluir la altura promedio de árboles dominantes o codominantes a una edad apropiada para su comercialización (Sharma y Reid, 2018) y se utiliza para estimar la altura del rodal con la finalidad de evaluar la calidad y las condiciones del terreno.
El IS se estima de datos tomados en campo, que provienen de: parcelas permanentes de muestreo, parcelas de medición temporal y datos de análisis troncales. Diversos investigadores han utilizado información proveniente de parcelas temporales y de análisis troncales para el ajuste de ecuaciones de altura dominante (a-d), dado que reduce el tiempo y costo; sin embargo, no descartan como la mejor opción la de parcelas permanentes para modelar el efecto a-d (Allen y Burkhart, 2015; Quiñonez-Barraza et al., 2020).
Las curvas del IS generadas con este tipo de enfoques deben de cumplir con algunas características o propiedades que son: polimorfismo, pauta de crecimiento sigmoide con un punto de inflexión, capacidad de alcanzar una asíntota horizontal a edades avanzadas, tener un sentido lógico (la altura dominante debe ser cero a la edad cero y la curva debe ser siempre creciente), ser invariantes con respecto al camino de simulación y con respecto a la edad de referencia (Bailey y Clutter, 1974).
Los métodos más utilizados para determinar la altura dominante e índice de sitio se basan en el enfoque de diferencias algebraicas (EDA O ADA) que involucra la sustitución de un parámetro del modelo base y expresarlo como una función del sitio (una combinación altura dominante-edad); sin embargo, su limitación se debe a que la mayoría de los modelos derivados son anamórficos o tienen una asíntota común (Cieszewski y Bailey, 2000); mientras que el modelo de diferencia algebraica generalizada (EDAG o GADA) ofrece una ventaja a la ecuación base, ya que puede ser expandida de acuerdo con diversas teorías, como la tasa de crecimiento y asíntota, haciendo que más de un parámetro de cada modelo dependa de la calidad de estación, y a la vez sea más flexible (Cieszewski, 2001, 2002, 2003).
En México se distribuye ampliamente una gran mezcla de especies con distintos estratos arbóreos (sobre todo incoetáneos), donde los estudios sobre productividad y crecimiento se practican en su mayoría para bosques de pino y encino al ser estos últimos altamente comerciales (Quiñonez-Barraza et al., 2015). La especie en estudio también es considerada importante en el sector forestal en los diferentes enfoques: económico, ecológico, ambiental, social y sobre todo en la dinámica natural; lo cual dio justificación a este estudio (Guzmán-Santiago et al., 2019).
Objetivos
La presente investigación tuvo como objetivo analizar curvas dinámicas de índice de sitio con la metodología EDAG en 12 Unidades de Manejo Ambiental (Umafor) para Abies religiosa en diferentes regiones de México.
Materiales y métodos
Área de estudio
Se tomó información de 12 Umafor en cinco entidades federativas, que son: Hidalgo (1303), Ciudad de México (1503, 1507, 1508, 1509, 1510), Michoacán (1604, 1605, 1607), Puebla (2105) y Tlaxcala (2901, 2902) (Comisión Nacional Forestal [Conafor], 2016).
Tamaño de muestra
Se obtuvo información de análisis troncales de 262 árboles dominantes-codominantes, mediante el muestreo destructivo que consistió en derribar, seccionar y medir los árboles. Para cada árbol se registraron las siguientes variables: diámetro normal (Dn, cm) medido a 1.3 m sobre el nivel del suelo, que fue medido con cinta diamétrica de 1 cm de resolución y forcípula Haglof Mantax Blue de la misma resolución, mientras que la altura total (At, m) fue medida con un flexómetro, con una resolución de 1 mm. Las primeras mediciones se realizaron en dos secciones de alturas de las secciones 0.30 m por encima del tocón, posterior a eso, la siguiente sección fue en el diámetro normal (1.30 m), y después las secciones fueron cortadas de manera constante a 2.54 m de longitud hasta llegar a la punta del árbol. La información relevante para los análisis respectivos se presenta en la Tabla 1.
Tabla 1 Estadísticos descriptivos de las variables utilizadas
| Umafor | Núm. De árboles | Mínimo | Promedio | Máximo | Desviación estándar |
| Altura total (m) | |||||
| 1303 | 26 | 14.50 | 32.95 | 42.10 | 5.97 |
| 1503 | 13 | 24.60 | 31.77 | 38.30 | 4.79 |
| 1507 | 14 | 20.32 | 32.68 | 40.61 | 5.79 |
| 1508 | 23 | 17.80 | 26.79 | 44.55 | 7.54 |
| 1509 | 20 | 22.30 | 34.47 | 42.00 | 5.85 |
| 1510 | 27 | 17.00 | 25.91 | 50.00 | 6.27 |
| 1604 | 29 | 23.20 | 32.71 | 43.00 | 4.25 |
| 1605 | 11 | 25.49 | 31.06 | 37.58 | 4.46 |
| 1607 | 29 | 10.75 | 25.44 | 36.00 | 7.63 |
| 2105 | 8 | 27.60 | 31.72 | 35.10 | 2.41 |
| 2901 | 36 | 13.40 | 24.00 | 39.20 | 6.79 |
| 2902 | 26 | 9.10 | 20.57 | 33.30 | 6.53 |
| Diámetro normal (cm) | |||||
| 1303 | 26 | 16.00 | 43.42 | 60.20 | 11.00 |
| 1503 | 13 | 41.00 | 55.00 | 75.00 | 9.92 |
| 1507 | 14 | 31.00 | 52.73 | 85.50 | 14.13 |
| 1508 | 23 | 29.00 | 49.48 | 79.00 | 13.24 |
| 1509 | 20 | 43.00 | 55.29 | 74.95 | 9.06 |
| 1510 | 27 | 27.00 | 50.56 | 83.00 | 16.76 |
| 1604 | 29 | 37.00 | 51.26 | 69.00 | 7.78 |
| 1605 | 11 | 44.00 | 53.36 | 61.00 | 5.16 |
| 1607 | 29 | 8.00 | 43.77 | 92.30 | 18.46 |
| 2105 | 8 | 30.80 | 47.57 | 68.70 | 13.00 |
| 2901 | 36 | 22.70 | 40.34 | 62.50 | 9.83 |
| 2902 | 26 | 18.20 | 33.46 | 86.50 | 17.06 |
| Edad (años) | |||||
| 1303 | 26 | 47.00 | 84.00 | 131.00 | 21.00 |
| 1503 | 13 | 34.00 | 50.00 | 88.00 | 16.00 |
| 1507 | 14 | 38.00 | 58.57 | 84.00 | 12.00 |
| 1508 | 23 | 26.00 | 58.26 | 126.00 | 28.00 |
| 1509 | 20 | 32.00 | 63.80 | 82.00 | 12.00 |
| 1510 | 27 | 30.00 | 59.96 | 85.00 | 16.00 |
| 1604 | 29 | 36.00 | 57.06 | 75.00 | 10.00 |
| 1605 | 11 | 36.00 | 56.72 | 96.00 | 20.00 |
| 1607 | 29 | 16.00 | 38.93 | 76.00 | 15.00 |
| 2105 | 8 | 54.00 | 75.62 | 115.00 | 21.00 |
| 2901 | 36 | 39.00 | 83.55 | 106.00 | 15.00 |
| 2902 | 26 | 25.00 | 52.00 | 114.00 | 23.00 |
Estimación de las alturas verdaderas
En ocasiones, la altura del corte de la sección no coincide con el comienzo del año, dado que la altura de cada sección de corta suele ser sobreestimada; lo cual sesga los cálculos posteriores (Fabio, Frattegiani y Manetti, 1994). Para solucionar este problema se utilizaron el algoritmo de Carmean (1972) y la fórmula modificada por Newberry (1991) para la troza final, que han sido empleadas por varios investigadores (Dyer y Bailey, 1987; Quiñonez-Barraza et al., 2015; Vargas-Larreta et al., 2017).
Los supuestos del método son dos: 1) el árbol crece a un ritmo constante entre dos secciones, 2) el corte se realiza, como media, en el centro del crecimiento en altura de un año. A continuación, se muestran las fórmulas empleadas para calcular la altura verdadera referente a cada parte del árbol.
Donde:
H1 y H2 = alturas de las secciones inferior y superior de la troza
N1 y N2 = número de anillos de las secciones inferior y superior de la troza
N0 = edad del árbol, es decir el número de anillos del tocón (en el tocón N0 = N1)
T0 = edad del árbol cuando alcanzó la altura H1, es decir N0 - N1
T = número entero de 1 a N1 - N2.
Metodología EDAG
El enfoque de diferencias algebraicas generalizada (EDAG o GADA) consiste en seleccionar la ecuación base e identificar los parámetros específicos del sitio. Posteriormente debe definirse de forma explícita cómo cambian los parámetros entre las distintas estaciones, para después reemplazarlos con las funciones explicitas de X, que es una variable independiente oculta que describe la productividad del sitio (resultado de factores ambientales y las prácticas de manejo y silvicultura) y nuevos parámetros.
En esta investigación se utilizó el modelo de Richards (1959) , la cual es flexible al tener una asíntota horizontal, presenta un patrón de crecimiento sigmoide, así como un punto de inflexión al modelar una relación altura dominante-edad.
Su forma general es la siguiente:
Donde:
H = altura dominante (m)
t = edad (años)
a1, a2, a3 = parámetros del modelo
Por otra parte, la notación general de las formulaciones EDAG, a1, … an se refieren a los parámetros del modelo base (parámetros locales que cambian de un sitio a otro), mientras que b1, …bm son los parámetros globales que permanecen constantes para todos los sitios. A continuación, se cita la expresión del modelo.
Donde:
Y = es el valor de la función a la edad t
Y0 = variable de referencia definida como el valor de la función a la edad t0.
A continuación, se deriva el modelo polimórfico con múltiples asíntotas (Ec. 4), en el cual más de un parámetro debe de ser una función de la productividad del sitio. Según Cieszewski (2004) no es posible obtener una ecuación de un modelo EDAG donde el parámetro a2 varíe con la calidad de sitio, ya que cuando a1 o a3 es una función de X y el parámetro a2 también es una función X, el modelo no puede ser resuelto para X.
Tomando en cuenta lo anterior, se concluye que la ecuación obtenida de Richards (1959) con la expresión EDAG, los parámetros a1 (asíntota) y a3 pueden considerarse dependientes de la calidad de estación (X). La expresión de la relación es la siguiente.
De esta manera, la ecuación de Richards se reestructura de la siguiente forma para dos pares de valores de altura dominante y edad.
Donde:
H0 = altura dominante a la edad inicial t0
H1 = altura dominante a la edad t1
Al despejar y agregar el logaritmo en ambos lados de la primera de las igualdades, se logra obtener expresión siguiente.
La solución X involucra las raíces de una ecuación cuadrática, y posteriormente se selecciona la función de la raíz más adecuada y se sustituye en la segunda expresión de la ecuación 7. De lo anterior, se deriva el polinomio de segundo grado en función de X el cual se puede despejar. El valor de X en la ecuación anterior, t0 y H0 toma los valores condicionales iniciales siguiente:
donde
La selección del valor de X0, involucra el valor positivo de la raíz cuadrada para luego sustituirla en segunda igualdad de las ecuaciones 7 con la finalidad de obtener la expresión EDAG, y así obtener las curvas dinámicas con polimorfismo y múltiples asíntotas (Ec. 10).
Donde:
X0 = está dada por la Ec. 5, b1, b2, b3 = parámetros globales
Método de ajustes
Se utilizó el método invariante denominado iterativo respecto a la edad de referencia, donde estima los efectos del sitio y a la vez asume que los datos contienen errores de medición y aleatorios (Cieszewski, 2003; Diéguez-Aranda, Álvarez González, Barrio-Anta y Rojo-Alboreca, 2005), dado que es ideal para base de datos grandes (Vargas-Larreta et al., 2010). Un primer paso consistió en la estimación de los parámetros globales, el cual considera de manera constante el parámetro local H0, el cual varía en cada árbol (se le asigna al principio la altura media observada a una edad base). Posteriormente, los valores estimados se tomaron como constantes y el parámetro H0 se estimó para cada árbol, y ser ajustado una vez más, utilizando como valor inicial para los parámetros locales la altura observada a la mitad de la edad del árbol. En seguida el valor estimado de cada árbol del parámetro local es una constante y, este se ajusta nuevamente para obtener nuevos parámetros globales.
Finalmente, el procedimiento se repite hasta que los parámetros globales queden estabilizados con valores significativos (p < 0.0001) y por ende haya una reducción de los errores (raíz del error medio cuadrático [REMCENT]) a través de varias iteraciones de manera consecutiva. El modelo de Richards fue ajustado con el procedimiento PROC MODEL del software System Statistical Analysis [SASENT] (2008), mediante la técnica de mínimos cuadrados ordinarios. Así mismo realizó la corrección de la autocorrelación (una relación entre los valores separados el uno del otro por un intervalo de tiempo dado) en los residuos (errores de predicción), para lo cual se utilizó el test de Dubin Watson (1971) (d), donde d es un valor comprendido entre 0 y 4; si el valor del estadístico d es próximo a 2, p = 0 (significa que no hay correlación), si se aproxima a 4, p < 0 y si se aproxima 0, p > 0.
Estadísticos de bondad de ajustes analizados
Los resultados obtenidos de cada ecuación fueron analizados mediante escalas numéricas y gráficas. A través de los residuales generados en la fase de ajuste se calcularon los estadísticos siguientes: el coeficiente de determinación (R2adj), el cual es deseable que alcance el valor de 1; en cuanto a REMC, es conveniente que tome el valor de cero. Por otra parte, el criterio de información akaike (CIA) se considera apropiado porque presenta un menor valor (Del Carmen-García, Castellana, Rapelli, Koegel y Catalano, 2014). La característica del sesgo (e̅,es) que busca que el promedio de los residuales sea igual a cero, con lo que se logra que el estimador sea centrado o insesgado (Amat-Rodrigo, 2016).
La expresión de los estadísticos de bondad de ajuste es la siguiente:
Donde:
SCR = suma de cuadrado del error
p = número de parámetros a estimar,
n = es el tamaño de muestra
ln = logaritmo natural
Yi = valores observados
Resultados
Ecuación dinámica
De acuerdo con la prueba de t-Student, los parámetros fueron estadísticamente significativos con valores de p < 0.0001, menores al valor crítico (a = 0.05); lo cual da certeza que el modelo de Richards es capaz de describir el patrón de crecimiento en altura dominante (H0) a una cierta edad de referencia para calificar los niveles de productividad, sin afectar las predicciones de índice de sitio (IS) o H0 en la modalidad polimórfica en las 12 Umafor, y que es corroborado por el análisis gráfico. De esta manera se describe que en la investigación se obtuvieron sesgos menores a 1 m, así como REMC menores a 1.2 m con coeficientes de determinación ajustados (R2adj) que explican más de 97% de la varianza total del crecimiento de la altura en función a la edad. Además, se obtuvieron CIA convincentes y valores de Durbin Watson aproximados a 2, que indican que no existe autocorrelación en forma general. Al utilizar el método EDAG o GADA, la ecuación base puede ser expandida sobre el crecimiento, lo cual hace que más de un parámetro del modelo dependa de la calidad de sitio con curvas a la vez flexibles y de múltiples asíntotas (Tabla 2).
Tabla 2 Parámetros estimados y estadísticos de ajuste de índice de sitio
| Estimadores de parámetros | Errores estándar | Bondad de ajustes | |||||||||
| Umafor | b1 | b2 | b3 | b1 | b2 | b3 | Sesgo (m) | REMC (m) | R2 j ad | CIA | Durbin Watson |
| 1303 | 0.0215 | -11.2831 | 48.7592 | 0.0012 | 0.9194 | 3.4411 | -0.0083 | 1.140 | 0.989 | 119.405 | 1.7945 |
| 1503 | 0.0450 | -34.4025 | 135.4675 | 0.0034 | 12.3273 | 45.1754 | 0.0065 | 0.897 | 0.992 | -35.165 | 1.8204 |
| 1507 | 0.0331 | -6.9173 | 32.9345 | 0.0024 | 1.6064 | 6.0675 | 0.0004 | 0.880 | 0.994 | -44.907 | 1.9375 |
| 1508 | 0.0245 | -11.2692 | 47.5785 | 0.0017 | 3.6285 | 13.5964 | -0.0479 | 1.077 | 0.988 | 42.953 | 1.6873 |
| 1509 | 0.0312 | -9.0155 | 39.8650 | 0.0023 | 2.1371 | 8.0381 | 0.0038 | 1.244 | 0.988 | 127.794 | 1.7303 |
| 1510 | 0.0298 | -5.0960 | 25.3848 | 0.0032 | 1.6802 | 6.0527 | 0.0106 | 1.608 | 0.969 | 303.256 | 1.8010 |
| 1604 | 0.0258 | -23.1380 | 98.1074 | 0.0021 | 4.4548 | 17.7117 | 0.0408 | 0.933 | 0.993 | -51.509 | 1.7900 |
| 1605 | 0.0295 | -18.3545 | 75.3568 | 0.0030 | 5.3515 | 19.7033 | -0.0153 | 0.774 | 0.993 | -70.247 | 1.6665 |
| 1607 | 0.0473 | -23.3945 | 98.1925 | 0.0028 | 3.7178 | 13.8686 | -0.0290 | 0.821 | 0.994 | -80.077 | 2.1486 |
| 2105 | 0.0389 | -11.7544 | 50.7659 | 0.0025 | 3.0581 | 11.0711 | 0.0149 | 0.681 | 0.996 | -91.401 | 1.9382 |
| 2901 | 0.0150 | -1.9402 | 11.4717 | 0.0019 | 0.3729 | 1.3434 | -0.0702 | 1.175 | 0.983 | 169.141 | 1.6599 |
| 2902 | 0.0165 | -16.9370 | 67.0074 | 0.0019 | 4.2031 | 14.9784 | -0.0353 | 1.226 | 0.978 | 102.709 | 1.8018 |
Familias de curvas de índice de sitio
Con base en los análisis estadísticos, se puede apreciar que el modelo describe adecuadamente el crecimiento en altura de forma biológica y se apega a las condiciones de diferentes niveles de productividad o índice de sitio. Así también, genera polimorfismo asintótico plausible al tener un punto de inflexión, así como predicciones de manera consistente e invariante de la edad de referencia.
En la figura 1 se aprecian las curvas obtenidas para los diferentes índices para cada Umafor a una edad base de 50 sobrepuestas en los gráficos de perfil de los árboles empleados en el ajuste, donde se muestra que las curvas siguen una trayectoria de los datos en los rangos de edades y que describen el crecimiento en un sentido biológico para las edades correspondientes. La edad base fue determinante para evitar discrepancias, dado que en edades jóvenes suelen ser susceptibles en los cambios ambientales. La calificación de los índices de sitio (IS) fue calidad baja (III), media (II) y alta (I).
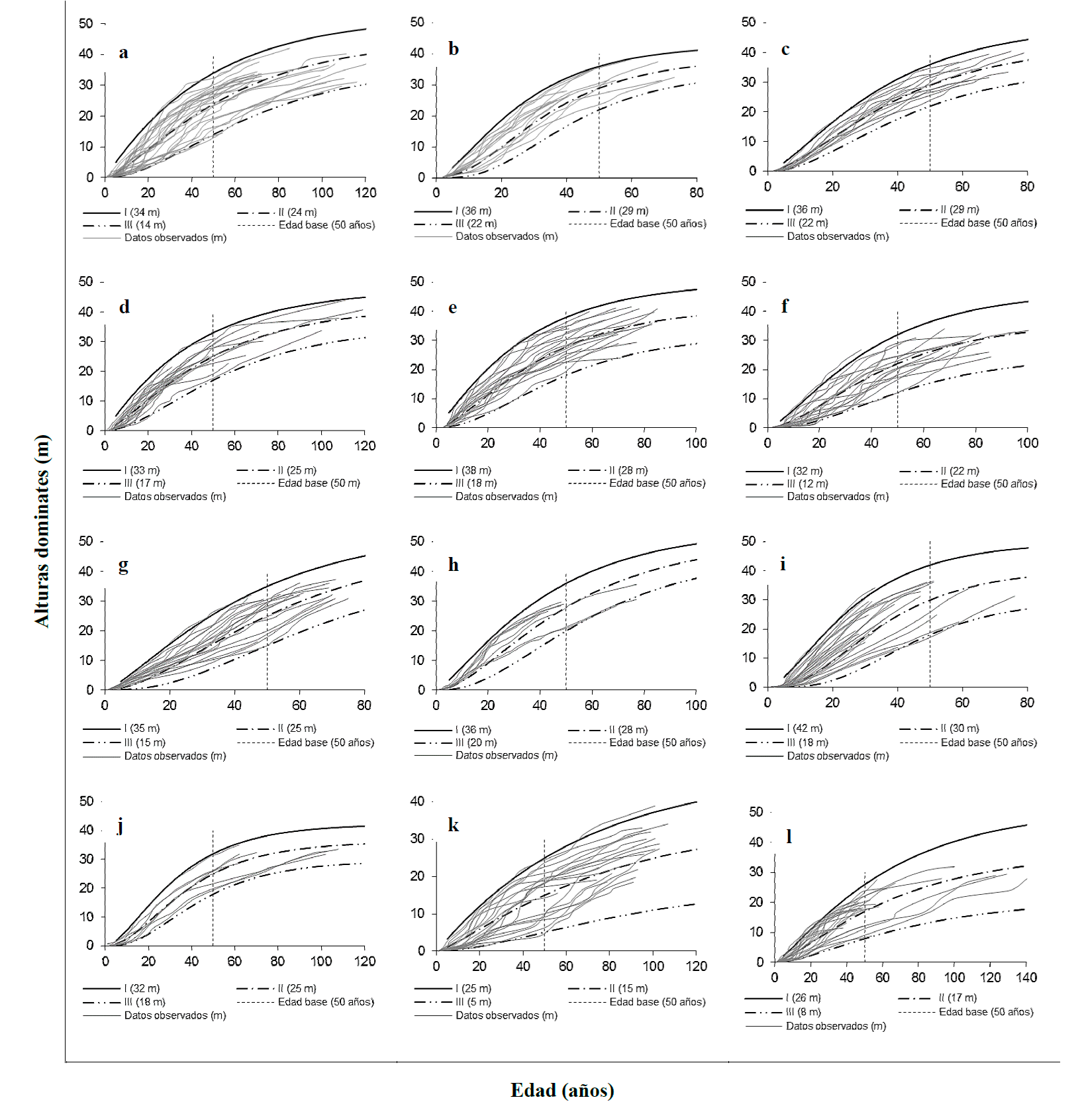
Figura 1 Curvas de índice de sitio, donde: a=1303, b=1503, c=1507, d=1508, e=1509, f=1510, g=1604, h=1605, i=1607, j=2105, k=2901, l=2902
Las calidades de sitio que se establecieron fueron variantes en las unidades de manejo, por lo que la escala cambió de un índice de sitio a otro, tomando los valores de 7 m, 8 m, 9 m, 10 m y 12 m. Las curvas presentaron buenos ajustes debido a la generalización del modelo, lo que permite observar curvas polimórficas con múltiples asíntotas. En este sentido, se destacan algunas características propias de las Umafor, donde la 1503 (B) y 1507 (C) son las que presentaron valores de IS más altos, y para los sitios de 2901 (K) inició desde los 5 (IS, m), seguida por la 2902 (L) partiendo de los 8 m. Así mismo, las asíntotas en sitios ricos (I) ocurren en su mayoría de 100 años en adelante como resultado de su ritmo de crecimiento (Fig. 1).
Análisis de residuos
Después de que se realizó el análisis estadístico del modelo, se puede complementar su pertinencia mediante el análisis gráfico; considerado como la forma más eficiente para evaluar la eficiencia. Con el método iterativo la expresión EDAG permitió el ajuste simultáneo, así como la comparación de la tasa de cambio, lo que permitió obtener excelentes resultados para cada Umafor, ya que se observa un patrón aleatorio de los residuos alrededor de la línea cero (modelo), evidenciando una varianza constante en las predicciones a distintas alturas (Fig. 2).
Discusión
La calidad en la bondad de ajuste obtenida en la investigación fue adecuada. Distintos autores revelan la ganancia significativa que se tiene al utilizar el método EDAG para la predicción y proyección del crecimiento a edades mayores a la utilizada. En este sentido, Vargas-Larreta et al. (2017) encontraron excelentes resultados para 97 especies incluidas de bosques tropicales y templados en México, mismas que se encuentra disponible en la plataforma digital denominado Sistema Biométrico Forestal [SiBiFor] (2016). En dicha investigación se observa que las bondades de ajustes referentes a los coeficientes (R2adj) así como la REMC comparten información similar respecto a Abies religiosa. De igual forma, se aporta información nueva para las Umafor 1510 (Ciudad de México), y la 2105 de Puebla. Los sistemas, en forma EDAG de crecimiento en altura dominante e índice de sitio son preferibles en los trabajos de manejo, así como en la planeación forestal (Kahriman, Sönmez y Gadow, 2018).
En este estudio se demuestra que el modelo de Richards es ligeramente superior estadísticamente a la ecuación de Korf polimórfico reportada en la plataforma SiBiFor para la región 1508 de México, sobre todo al reducir el error (REMC) utilizando la edad de referencia de 50 años. Debido a lo anterior, Vargas-Larreta, Aguirre-Calderón, Corral-Rivas, Crecente-Campo, y Diéguez-Aranda (2013) recomiendan seleccionar una edad base mayor para no generar inconvenientes, ya que en edades jóvenes la clasificación de la calidad de sitio muchas veces puede verse afectada la estimación de la altura total por las condiciones ambientales.
Los factores ambientales, el manejo silvícola, así como las características genéticas de las especies, tienden a influir en los patrones de crecimiento entre los sitios (Montero, Ugalde y Kanninen, 2001; Mora, Muñoz, Meza y Fonseca, 2015; Camacho, Alvarado y Fernández-Moya, 2016; Camacho, Alvarado y Fernández-Moya, 2017). Yilmaz (2019) concluye que el índice de sitio varía con la altitud y el grado de inclinación de la región, por lo cual es importante el conocimiento en las áreas potenciales para el manejo y sobre todo para el establecimiento de plantaciones.
El propósito de conocer el patrón de crecimiento en altura dominante de los árboles es para calificar la productividad del sitio y no solo para predecir la altura del rodal a una edad de referencia (Clutter et al., 1983; Hernández-Ramos et al., 2015). De acuerdo con García (2011) y Vargas-Larreta et al. (2017) , los sistemas de cómputo son herramientas indispensables, ya que ofrecen la ventaja para simular la dinámica forestal, y de esta forma los manejadores de bosques puedan utilizar el sistema de ecuaciones para definir los regímenes ideales para la especie en estudio.
Stankova y Diéguez-Aranda (2012) , Galindo-Soto, Vargas-Larreta, Hernández y Cruz-Cobos (2017) , Westfall, Hatfield, Sowers y O’Connell (2017) y Hernández-Cuevas et al. (2018) obtuvieron resultados similares a los de esta investigación sobre la capacidad de precisión del modelo con este enfoque (Stankova y Diéguez-Aranda, 2012), evidenciando la gran flexibilidad que tiene (Tang et al., 2016); en donde las curvas permiten clasificar los bosques naturales con base en su potencial, mediante las condiciones de manejo de distintas especies (Delgado-Caballero et al., 2009).
Este método fue empleado también en el trabajo de Quiñonez-Barraza et al. (2015) que obtuvo excelentes resultados para especies de Pinus arizonica, P. durangensis, P. teocote, P. leiophylla, y P. ayacahuite en rodales mezclados con la misma edad de referencia (60 años). Tamarit-Urias, Santos-Posadas, Aldrete, Valdez-Lazalde y Ramírez-Maldonado (2014) difundieron sus aportaciones científicas sobre las plantaciones de Tectona grandis en Campeche, México. De igual forma Rodríguez-Carrillo, Cruz-Cobos, Vargas-Larreta y Hernández (2015) encontraron altos ajustes estadísticos sobre táscate (Juniperus deppeana Steud.), lo mismo que Castillo-López et al. (2013) al estudiar Pinus arizonica, P. durangensis, P. leiophylla y P. teocote; ambos realizados en Durango. Las investigaciones de Carrero, Jerez, Macchiavelli, Orlandoni y Stock (2008) y de Attis-Beltrán et al. (2015) para especies de Eucalyptus urophylla y bosques mixtos de Nothofagus alpina y N. obliqua (Neuquén, Argentina), reportan resultados similares a los obtenidos en este trabajo.
Conclusiones
El modelo de Richards, utilizado mediante la metodología EDAG, mostró buenos resultados en cuando a la bondad de ajuste para modelar las curvas de índice de sitio de altura dominante-edad para Abies religiosa con base en las diferentes escalas de cambio; ya que este modelo considera las características biológicas, por lo que le facilita describir las relaciones que existen entre las variables en un sentido biológico.
Las ecuaciones generadas son de tipo polimórfico con múltiples asíntotas, invariante con respecto a la edad base, por lo que estiman de forma directa la altura dominante y el índice de sitio a cualquier edad o altura.
Mediante muestras de análisis troncales se obtuvieron resultados verídicos, por lo que se recomienda el uso de esta técnica para investigaciones de otras especies.
Las expresiones matemáticas son recomendables para ser empleadas en estudios de planes de manejo, para clasificar la productividad maderable de rodales de distintas edades y pueden incorporarse en modelos de rendimiento y crecimiento de las distintas regiones.











 nueva página del texto (beta)
nueva página del texto (beta)



