División I

 

Evaluación empírica de la reflectometría de dominio temporal para estimar la humedad en dos suelos de origen volcánico

 

Empirical evaluation of the time domain reflectometry for water content measurement in two volcanic soils

 

M. Bravo-Espinosa¹*, B. Serrato-Barajas¹, L. Fregoso-Tirado¹ y L. Medina-Orozco²

 

¹ Campo Experimental Uruapan-INIFAP. Av. Latinoamericana 1101. 60500 Uruapan, Michoacán, México. ^*Autor responsable (bravo.miguel@inifap.gob.mx).

² Facultad de Biología. Universidad Michoacana de San Nicolás de Hidalgo. 58060 Morelia, Michoacán, México.

 

Recibido: enero de 2008.
Aceptado: enero de 2009.

 

RESUMEN

La reflectometría de dominio temporal (TDR) es una técnica electromagnética indirecta, rápida, no destructiva y precisa para estimar el contenido de humedad del suelo. Sin embargo, la aplicabilidad de esta técnica en suelos volcánicos y en suelos de textura fina fue documentada como imprecisa. El objetivo de este trabajo ha sido evaluar la función de calibración del fabricante del equipo TDR, definida por la ecuación universal, en un Acrisol y en un Andosol; además de generar una función de calibración con mejor ajuste que la obtenida con la ecuación universal. Se usó un equipo TDR modelo 6050X1 Trase System para estimar la humedad volumétrica en dos tipos de suelo. La recolección de muestras de suelo para la determinación gravimétrica se realizó con una barrena de gusano y la densidad aparente del suelo se determinó con el método de excavación. Las mediciones con el TDR y la obtención de muestras de suelo se realizaron simultáneamente con una frecuencia semanal. Se aplicó el coeficiente de desigualdad para evaluar la desviación entre las tendencias de los valores predichos (θ_Pred) por la ecuación universal y los observados (θ_Obs), mientras que la tasa de discrepancia se usó para evaluar la capacidad de la ecuación universal para reproducir valores individuales. En los dos tipos de suelo la relación K_a contra θ_Obs se desvió de la función universal definida por la relación K_a contra θ_Pred; la mayor desviación se presentó en el Andosol, en el cual se observó que la ecuación universal subestimó la tendencia de los valores medidos. Se obtuvieron dos funciones de calibración para las condiciones de los dos suelos bajo estudio.

Palabras clave: ecuación universal, Andosol, Acrisol, sistema de año y vez.

 

ABSTRACT

Time domain reflectometry (TDR) is an indirect electromagnetic technique for measuring soil water content; it is fast, nondestructive, and accurate. However, the applicability of this technique particularly in volcanic and clayey soils was reported to be imprecise. The objective of this study was to evaluate the TDR manufacturer's calibration function, defined by the universal equation, in two different soils (Andisol and Acrisol), and furthermore, to estimate an empirical calibration function that is more accurate than the universal equation. A Trase System TDR model 6050X1 was used to estimate volumetric water content in two types of soils. Soil samples for gravimetric water content were collected with a screw auger, and soil bulk density was estimated by the excavation method. Weekly, measurements were made of water content by the TDR and gravimetric sampling simultaneously. The inequality coefficient was used to assess the deviation between the trend of predicted values (θ_Pred) by the universal equation and the trend of measured values (θ_Obs), whereas the discrepancy ratio was used to evaluate the universal equations ability to reproduce individual measured data. In both soils the relation K_a against θ_Obs deviated from the universal function defined by the relation K_a against θ_Pred; this deviation was greater in the Andisol than in the Acrisol; the universal equation underestimated the trend of measured values. Two calibration functions for the conditions of the two soils under study were obtained.

Keywords: universal equation, Andisols, Acrisols, short-fallow system.

 

INTRODUCCIÓN

El manejo del contenido de humedad en el suelo es una variable importante para lograr una producción agrícola óptima, y se requiere, además, en estudios hidrológicos para apoyar la estimación de balances de agua, entre muchas otras aplicaciones edafológicas. El método estándar de medición del contenido de humedad del suelo es el método gravimétrico, el cual se usa para calibrar y evaluar a los demás métodos (Brady y Weil, 1999; SEMARNAT, 2002). Existen varios métodos que son rápidos y no destructivos, como el aspersor de neutrones o la técnica de atenuación de rayos gama, pero generan riesgos al usuario por la exposición a las radiaciones; además, el primero requiere de calibraciones para cada sitio de uso y es muy sensible a otras propiedades del suelo. El segundo es impreciso en campo (Jury et al., 1991).

Los métodos que estiman el contenido de agua con base en propiedades dieléctricas del suelo superan las imprecisiones de aquéllos basados en radiaciones. Uno de estos métodos es el de TDR. El fundamento de este método es que la constante dieléctrica del agua es muy alta (80) en comparación con la del suelo completamente seco (2-4) y del aire (1). Esta disparidad de la constante dieléctrica hace que los métodos basados en dicha constante sean poco sensibles a los componentes del suelo. La constante dieléctrica depende de la frecuencia del campo eléctrico que se aplique. Para el caso del TDR, el valor de la constante dieléctrica aparente (K_a) no se determina para todas las frecuencias, sino que se determina sólo para el rango más sensible de frecuencias, que para suelos húmedos se ubican entre 50 y 10 GHz (Roth et al., 1990). El TDR es un método indirecto, rápido, no destructivo y preciso para determinar la humedad del suelo, el cual es ampliamente usado en estudios de escala puntual (Walker et al., 2004).

Para predecir el contenido volumétrico de humedad del suelo (θ) con un equipo TDR, se requiere de una función que relacione la constante dieléctrica aparente (K_a) con 9. La función más usada ha sido la polinómica de tercer grado desarrollada por Topp et al. (1980), conocida como ecuación universal, cuya principal ventaja es que no requiere de la determinación de ningún parámetro del suelo. Los equipos TDR son entregados por el fabricante con esta función de calibración:

Sin embargo, esta ecuación no ha mostrado buena aplicabilidad en suelos volcánicos (Miyamoto y Chikushi, 2000) ni en suelos de textura fina (Dasberg y Hopman, 1992; Yu et al., 1999). Por ello, se ha sugerido que se realicen estudios de calibración para generar funciones específicas a los tipos de suelo y condiciones de uso del equipo TDR (Jackson, 2004).

Para medir el contenido de agua de la capa superior del suelo con el TDR, se introducen en el suelo dos varillas metálicas paralelas que actúan como líneas de transmisión de las ondas electromagnéticas que se envían desde el reflectómetro. El volumen de suelo muestreado por el par de varillas es aproximadamente cilíndrico, su radio es la separación que existe entre las dos varillas. La longitud de éstas es la profundidad muestreada. La velocidad de propagación de las ondas electromagnéticas se determina con base en el tiempo de tránsito desde el extremo de las varillas hasta el reflectómetro. El valor de la constante dieléctrica aparente (K_a) se calcula a partir de la siguiente expresión:

donde: t = el tiempo de tránsito de la onda electromagnética (ns, nanosegundos); c = la velocidad de la luz (cm ns^-1); L = la longitud de la línea de transmisión (cm).

 

MATERIALES Y MÉTODOS

El presente trabajo se desarrolló en dos sitios ubicados en La Ciénega 19° 35' 19.8" N y 101° 12' 20" W y La Cortina 19° 30' 45" N y 101° 12' 12.8 W, que se localizan en la subcuenca de Cointzio, al sur de la ciudad de Morelia, Michoacán. La formación geológica del área está constituida por andesitas; los principales tipos de relieve son lomeríos altos y bajos. Hidrológicamente, esta zona aporta sus escurrimientos a la presa de Cointzio. La temperatura media anual es de 18 °C y la precipitación media anual de 900-1100 mm, concentrada en los meses de junio a septiembre. Los suelos dominantes son volcánicos y se clasifican como Andosoles y Acrisoles. Los usos del suelo predominantes son el agrícola, pastoreo y forestal. Los cultivos que se practican son maíz, bajo temporal o humedad residual, y sólo de temporal la asociación maíz-frijol y avena. Las prácticas de labranza se realizan con tractor (barbecho y surcado) y con yunta o tiro animal (surcado y labores de cultivo). El Cuadro 1 presenta las características de la capa superficial (0-30 cm) de los dos tipos de suelo bajo estudio.

En cada tipo de suelo bajo estudio se consideró un uso de descanso, el cual es parte del sistema de producción de Año y Vez (AV), común en la subcuenca de Cointzio. Se usó un equipo TDR modelo 6050X1 Trase System (Soilmoisture Equipment Corp.) para medir la humedad volumétrica en campo. En cada suelo, bajo el manejo indicado, se colocaron verticalmente cuatro pares de varillas metálicas para evaluar el contenido de agua de la capa superficial de 0-30 cm de profundidad. La distribución de los pares de varillas se realizó en línea recta a lo largo de la parcela. Las varillas de acero tuvieron un diámetro de 2.0 cm con 30 cm de largo y una separación entre ellas de 4.5 cm. La recolección de muestras de suelo para la determinación gravimétrica se realizó manualmente con una barrena de gusano a una separación no menor de 10 cm, con relación a las varillas para no afectar las mediciones del TDR por la formación de bolsas de aire (Jones et al., 2002). Tanto las mediciones con el TDR como la obtención de muestras de suelo se realizaron simultáneamente, con una frecuencia semanal de octubre a diciembre de 2006. No se midió la humedad del suelo de enero a marzo en ninguno de los suelos, y sólo se realizaron mediciones en abril de 2007 en el Andosol para incluir valores cercanos a punto de marchitez permanente (PMP). La densidad aparente del suelo se determinó en campo para la profundidad 0-30 cm con el método de excavación (Blake, 1965). Se realizaron cuatro repeticiones de la densidad aparente distribuidas en puntos cercanos al lugar donde se instalaron las varillas del TDR.

Se compararon la humedad gravimétrica medida con el TDR (θ_Pred) y la humedad volumétrica (θ_Obs) definida a partir del producto de la densidad aparente y la humedad gravimétrica. Se aplicaron dos tipos de pruebas estadísticas para evaluar la predicción con la ecuación universal, de la humedad volumétrica en los dos tipos de suelos (Pindyck y Rubinfeld, 1991). La primera prueba fue el coeficiente de desigualdad (CD), el cual mide la desviación entre las tendencias de los valores predichos (θ_Pred) y los observados (θ_Obs) tomando únicamente valores entre 0 y 1. Si CD = 0, entonces θ_Pred = θ_Obs, por lo tanto, hay un ajuste perfecto; si CD = 1, la ecuación carece de valor predictivo. El CD se calcula por la ecuación:

Los términos de esta ecuación se describieron con anterioridad. La segunda prueba fue la tasa de discrepancia (TD), la cual mide la capacidad para reproducir valores puntuales o individuales; se define como el cociente de las mediciones individuales predichas y observadas. Explícitamente: TD = θ_Pred θ_Obs^-1.0. Si TD = 1, significa que la ecuación predice exactamente los valores individuales observados. Para cada tipo de suelo se obtuvo la media de la tasa de discrepancia. El ajuste de los valores θ_Obs a una función polinomial se realizó con el programa estadístico JMP, versión 3.2.2 (SAS Institute, 1997).

 

RESULTADOS Y DISCUSIÓN

La densidad aparente del suelo fue mayor en el Acrisol (La Ciénega) que en el Andosol (La Cortina); se obtuvieron valores promedio de 1.18 y 0.75 Mg m^-3, respectivamente. En el Cuadro 2 se presentan las principales medidas descriptivas de las bases de datos generadas en el presente trabajo.

La desviación entre la tendencia de los valores predichos (θ_Pred) por el TDR (ecuación universal) y los valores observados o medidos (θ_Obs) fue menor en el Acrisol que en el Andosol (Cuadro 3). Asimismo, la capacidad del TDR para reproducir valores individuales observados fue mejor en el Acrisol; sin embargo, es claro que el TDR tiende a subestimar los valores observados de humedad volumétrica, siendo este comportamiento más notable en el Andosol (Cuadro 3).

Las Figuras 1 y 2 muestran la dispersión de valores de la constante dieléctrica aparente, la cual se leyó directamente de la pantalla de control del equipo TDR contra el contenido volumétrico de agua para los dos tipos de suelos, ambos con manejo de descanso (AV). En los dos tipos de suelo se observa una menor dispersión de datos a medida que aumenta el contenido de humedad en el suelo, aunque esta tendencia fue mayor en el Acrisol que en el Andosol. La curva tenue representa el ajuste de la curva de calibración de Topp et al. (1980) (Ecuación 1) a los valores mencionados. La función de respuesta con línea más obscura, se obtuvo ajustando un modelo polinomial de tercer grado. La relación K_a contra θ_Obs en el rango de valores medidos (Figuras 1 y 2) se desvió de la función de calibración o ecuación universal. La menor desviación se presentó en el Acrisol y la mayor ocurrió en el Andosol, en el cual se observó que la ecuación universal subestimó la tendencia de valores medidos para este suelo. Esta tendencia de subestimar la humedad volumétrica en Andosoles coincidió con los estudios reportados por Miyamoto et al. (2001).

 

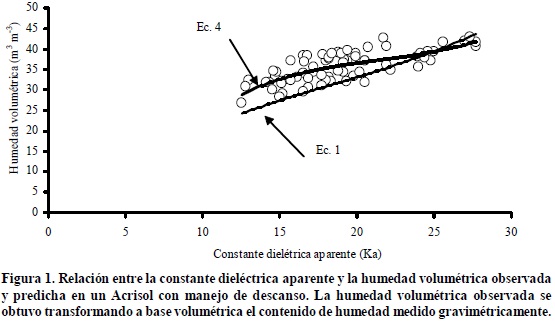
Las funciones polinomiales de tercer grado que mostraron mejor ajuste para el Acrisol y Andosol fueron, respectivamente:

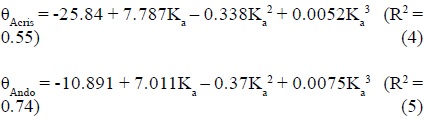
Diversas propiedades del suelo posiblemente afectaron el comportamiento dieléctrico de la capacidad de retención de agua de los dos suelos en estudio; esto se manifestó en la dispersión de datos y, por ello, la precisión de las funciones matemáticas obtenidas en este trabajo fue reducida. Malicki et al. (1996) y Perdok et al. (1996) concluyeron que una función que no incorpore en su estructura el efecto de la porosidad, densidad aparente o la superficie específica, producirá errores significativos en la estimación dieléctrica del contenido de humedad, en particular en suelos de textura franca o arcillosa. Para generar modelos lineales que pueden ser más precisos y más simples que las funciones polinomiales, también fue sugerido evaluar índices alternos a la constante dieléctrica, como el generado por Whalley (1993). Esto sugiere que para el futuro se deberán desarrollar modelos que incluyan variables que gobiernen las propiedades dieléctricas del suelo para mejorar su capacidad predictiva.

 

CONCLUSIONES

La técnica de la reflectrometría de dominio temporal (TDR) para determinar la humedad volumétrica fue más imprecisa en el Andosol que en el Acrisol, lo cual se comprobó porque el conjunto de valores medidos en ese suelo se desvió de la tendencia que mostró la función universal, definida por la relación de la constante dieléctrica aparente (K_a) contra el contenido volumétrico predicho (θ_Pred), porque los valores individuales medidos en el Andosol fueron subestimados por dicha función universal. Se construyeron dos funciones de calibración para las condiciones de los dos suelos en estudio, con mejor ajuste que el estimado con la ecuación universal.

 

AGRADECIMIENTOS

Los autores expresan su agradecimiento al fondo sectorial CONACYT-SEMARNAT por haber financiado este trabajo, el cual formó parte del proyecto: Degradación y restauración de suelos con enfoques participativos en la cuenca de Coíntzio, Michoacán (SEMARNAT-2004-C01-304/A-1).

 

LITERATURA CITADA

Blake, G. R. 1965. Bulk density. pp. 377-378. In: C. A. Black (ed.).Methods of soil analysis. Part I. Agronomy 9. American Societyof Agronomy. Madison, WI, USA.         [ Links ]

Brady, N. C. and R. W. Weil. 1999. The nature and properties of soils. Prentice Hall. Upper Saddle River, NJ, USA.         [ Links ]

Dasberg, S. and J. W. Hopman. 1992. Time domain reflectometry calibration for uniformly and nonuniformly wetted sandy and clayey soils. Soil Sci. Soc. Am. J. 56: 1341-1345.         [ Links ]

Jackson, S. H. 2004. In situ calibration of time domain reflectometry sensors in multiple soils. Comm. Soil Sci. Plant. Anal. 35: 865-878.         [ Links ]

Jones, S. B., J. M. Wraith, and D. Or. 2002. Time domain reflectometry measurement. Principles and applications. Hydrol. Process. 16: 141-153.         [ Links ]

Jury, W. A., W. R. Gardner, and W. H. Gardner. 1991. Soil physics. John Wiley. New York, NY, USA.         [ Links ]

Malicki, M. A., R. Plagge, and C. H. Roth. 1996. Improving the calibration of dielectric TDR soil moisture determination taking into account the solid soil. Eur. J. Soil Sci. 47: 357-366.         [ Links ]

Miyamoto, T. and J. Chikushi. 2000. Relations between soil water content and apparent dielectric constant evaluated by dielectric mixing models. Trans. Jpn. Irrigation, Drainage Reclamation Eng. 206: 57-62.         [ Links ]

Miyamoto, T., R. Kobayashi, T. Annaka, and J. Chikushi. 2001. Applicability of multiple length TDR probes to measure water distributions in an Andisol under different tillage systems in Japan. Soil Tillage Res. 60: 91-99.         [ Links ]

Perdok, U. D., B. Kroesbergen, and M. A. Hilhorst. 1996. Influence of gravimetric water content and bulk density on the dielectric properties of soil. Eur. J. Soil Sci. 47: 367-371.         [ Links ]

Pindyck, R. S. and D. L. Rubinfeld. 1991. Econometric models and economic forecasts. McGraw-Hill. New York, NY, USA.         [ Links ]

Roth, K., R. Schulin, H. Fluhler, and W. Attinger. 1990. Calibration of time domain reflectometry for water content measurement using a composite dielectric approach. Water Resour. Res. 26: 2267-2273.         [ Links ]

SAS Institute. 1997. JMP User's Guide, Versión 3.2.2. SAS Institute Cary, NC, USA.         [ Links ]

SEMARNAT (Secretaría del Medio Ambiente y Recursos Naturales). 2002. Norma Oficial Mexicana NOM-021-SEMARNAT-2000. Especificaciones de fertilidad, salinidad y clasificación de suelos, estudio, muestreo y análisis. Diario Oficial de la Federación. http://www.semarnat.gob.mx/leyesynormas/normasoficialesmexicanasvigentes/Recursos%20Naturales/NOM-021-RECNAT-2000.pdf (Consulta: noviembre 18, 2006).

Topp, G. C., J. L. Davis, and A. P. Annan. 1980. Electromagnetic determination of soil water content measurement in coaxial transmission line. Water Resour. Res. 16: 574-582.         [ Links ]

Walker, J. P., G. R. Willgoose, and J. D. Kalma. 2004. In situ measurement of soil moisture: a comparison of techniques. J. Hydrol. 293: 85-99.         [ Links ]

Whalley, W. R. 1993. Considerations of the use of time-domain reflectometry (TDR) for measuring soil water content. J. Soil Sci. 44: 1-9.         [ Links ]

Yu, C., W. Warrick, and M. H. Conklin. 1999. Derived functions of time domain reflectometry for soil moisture measurements. Water Resour. Res. 35: 1789-1796.         [ Links ]