Introducción
Dentro de la bibliotecología y ciencias de la información, la clasificación de documentos se ha visto como una tarea intelectual y compleja. Tiene como finalidad facilitar la recuperación de documentos dentro de las unidades y centros de información, basada en una localización física del material, representada por áreas temáticas y sistemas alfanuméricos de clasificación.
Tradicionalmente, esta tarea es efectuada de forma manual por bibliotecarios profesionales, dando como resultado palabras clave en forma de descriptores o encabezamientos de materia que son utilizados como puntos de acceso temáticos en la búsqueda de información (Contreras 2018, 112).
Clasificar los documentos de forma manual es una tarea que conlleva tiempo y esfuerzo adicional por parte de los profesionales de la información, considerando que en algunos casos deben conocer o estar familiarizados con el área de conocimiento de un documento, con el objetivo de identificar y comprender con mayor precisión su contenido (Polo Bautista, y Martínez Acevedo 2021, 161).
El crecimiento masivo de documentos en los medios digitales también dificulta el proceso de clasificarlos e indizarlos manualmente. Este es el problema en la llamada sobrecarga de información: más que referirse al problema relacionado con la gran cantidad de información que existe actualmente, éste apunta hacia la dificultad para acceder a ella y gestionarla de manera adecuada (Levy 2005, 283).
Para solucionar estas problemáticas, se han desarrollado métodos para organizar y clasificar estos documentos de manera automática (Aljedani, Alotaibi, y Taileb 2020, 694). Estos métodos y modelos computacionales son relevantes en una gran variedad de tareas de organización y gestión de la información (Alfaro, y Allende 2020, 551), con énfasis en el análisis automático de grandes datos textuales y la identificación de patrones lingüísticos asociados con las principales áreas temáticas de un documento.
Los métodos de clasificación automática de documentos pueden diversificar y mejorar los procesos de organización de la información dentro del área de bibliotecología y ciencias de la información, permitiendo procesar una amplia gama de formatos de documentos y creando servicios especializados orientados en la gestión de información digital y electrónica.
El algoritmo implementado en este trabajo puede servir como base para el desarrollo de nuevos métodos de clasificación automática de documentos dentro del área de bibliotecología y ciencias de la información, a partir de la utilización de grandes modelos de lenguaje. De este modo, el rendimiento de estos algoritmos de clasificación puede ser indistinguible al compararse con la misma tarea realizada por un bibliotecario profesional.
"En la actualidad existen diversas técnicas de aprendizaje automático que son utilizadas para clasificar documentos de forma automática, y cada una tiene características propias que permiten resolver diferentes problemas" (Silva 2021, 27). La clasificación es un tema fundamental en el aprendizaje automático; su objetivo es construir algoritmos a partir del entrenamiento de un conjunto de datos que permitan predecir la etiqueta o área temática que le corresponde a un documento (Zhang 2004, 562).
El algoritmo Naïve Bayes es una técnica de aprendizaje automático supervisado, basada en el teorema de Bayes y la teoría de la probabilidad [...]. La clasificación bayesiana es una herramienta estadística para categorizar un conjunto de datos, a través de la predicción de una etiqueta o categoría definida para un documento (Marikani, y Shyamala 2020, 296).
Este algoritmo ha sido aplicado en varios dominios del conocimiento en las últimas décadas debido a su estructura sencilla y su rendimiento. Su simplicidad surge fundamentalmente con la suposición de que cada par de atributos es condicionalmente independiente con respecto a la información de la clase o área temática correspondiente (Harzevili, y Alizadeh, 2018: 516).
El algoritmo utilizado en este trabajo es el Multinomial de Naïve Bayes o NB multinomial, un modelo de aprendizaje automático probabilístico. La utilización del algoritmo permitió el desarrollo del sistema de clasificación automática de documentos en el área de Ciencias de la Vida y Biomedicina. Los detalles asociados a la fundamentación matemática del algoritmo se describen en la sección 2.2.1 sobre la metodología.
Seleccionamos el área de Ciencias de la Vida y Biomedicina por dos razones principales: i) es un área de investigación poco utilizada en este tipo de aplicaciones computacionales; y ii) es el campo de conocimiento que tiene más categorías (76) dentro de las áreas de investigación del Web of Science (Clarivate Analytics 2020). De las 76 categorías que implementa esta área de investigación, tomamos en cuenta 21 (Tabla 1).
Tabla 1 Categorías del área de investigación en Ciencias de la Vida y Biomedicina
| Categorías del área de investigación en Ciencias de la Vida y Biomedicina | ||||
|---|---|---|---|---|
| Biología del Desarrollo | Biología marina y de agua | Biotecnología y Microbiología Aplicada |
Medicina General e Interna |
Pesca |
| Biofísica | Medicina Integrativa y Complementaria |
Biología Evolutiva | Ciencias Ambientales y Ecología |
Medicina de Urgencias |
| Medicina Legal | Biodiversidad y Conservación |
Geriatría Gerontología |
Hematología | Enfermedades infecciosas |
| Silvicultura | Ciencias y servicios sanitarios |
Entomología | Dermatología | Inmunología |
| Ciencias de la Vida y Biomedicina - Otros Temas |
||||
Fuente. Adaptado de Áreas de investigación
(Categorías/Clasificación) por Clarivate Analytics, 2020
El resto de este trabajo está organizado de la siguiente manera: en la sección dos se describe la metodología utilizada; en la sección tres se presentan los resultados obtenidos; en la sección cuatro se presenta una discusión relacionada con el estado del arte; y en la sección cinco se muestran las conclusiones generales y los trabajos futuros.
Metodología
Utilizamos el algoritmo de clasificación Naïve Bayes Multinomial para analizar la correlación entre los temas en el área de Ciencias de la Vida y Biomedicina, y los resúmenes de un corpus de 10 167 artículos recuperados del Web of Science. Realizamos una prueba de rendimiento del algoritmo aplicada a 5 581 resúmenes, para medir su precisión, exhaustividad y exactitud.
Para el desarrollo y la implementación del algoritmo seguimos los siguientes procedimientos: i) Recopilación del corpus (Tabla 2); ii) Configuración del programa (Tabla 3); y iii) Codificación del algoritmo (Tabla 4).
Tabla 2 Recopilación del corpus
| Etapa | Procedimiento |
|---|---|
| 1 | Compilación del corpus de entrenamiento. Conformado por 10 167 artículos so- bre Ciencias de la Vida y Biomedicina obtenidos a través del Web of Science. |
| 2 | Compilación del corpus de prueba. Conformado por 5 581 artículos sobre Cien- cias de la Vida y Biomedicina obtenidos a través del Web of Science. |
Tabla 3 Configuración del programa
| Etapa | Procedimiento |
|---|---|
| 1 | Creación de una cuenta de correo electrónico de Google1. Permitirá tener acceso gratuito a los servicios de Google Drive2 y Google Colaboratory3. |
| 2 | Subir los corpus de artículos de investigación (entrenamiento y prueba) a Google Drive. |
| 3 | Comenzar un nuevo proyecto (notebook) en Google Colaboratory. |
Tabla 4 Codificación del algoritmo
| Etapa | Procedimiento |
|---|---|
| 1 | Importar los corpus de entrenamiento4 y prueba5 a través de Google Drive. |
| 2 | Implementar los módulos Pandas para el análisis de datos (McKinney 2010; The pan- das development team 2020) y Matplotlib para generar visualizaciones de los datos (Hunter 2007). |
| 3 | Implementar el módulo Scikit-learn para utilizar el algoritmo Naïve Bayes Multinomial y generar métricas de rendimiento (Pedregosa et al. 2011). |
| 4 | Implementar el módulo Seaborn para apoyar en la generación de visualizaciones de datos (Waskom 2021). |
| 5 | Exportar el archivo que se generó como resultado tras la ejecución del algoritmo6. |
Detalles del corpus
La parte inicial de este trabajo consistió en la compilación de un corpus de registros bibliográficos de artículos en el área de Ciencias de la Vida y Biomedicina en el periodo 1997-2017, a través del Web of Science. Se recuperaron 10 167 artículos correspondientes a 21 (Tabla 1) de las 76 categorías del área de investigación antes mencionada.
Este corpus de artículos científicos contiene como idioma hegemónico el inglés, seguido de otros idiomas, como español, alemán, ruso y portugués. Fue utilizado en forma de datos de entrenamiento para analizar la correlación entre los contenidos de los resúmenes y los temas o categorías del área de investigación en Ciencias de la Vida y Biomedicina.
La prueba del rendimiento del algoritmo se aplicó a un corpus distinto del anterior, conformado por 5 581 registros bibliográficos de esta misma área de investigación, en el periodo 2002-2016. Contiene como idioma principal el inglés y en menor medida el español, el alemán y el ruso. Fue utilizado como datos de prueba para medir el grado de precisión, exhaustividad y exactitud del algoritmo.
Fundamentación matemática
Según Manning, Raghavan y Schütze (2009, 258) el algoritmo Naïve Bayes Multinomial describe la probabilidad de que un documento d esté en la clase c, tal como se muestra en la Fórmula 1:
Donde P(tkǀc) es la probabilidad condicional del término tk que se produce en un documento de la clase c. Interpretamos P(tkǀc) como medida de la cantidad de pruebas tk que contribuye a c como la clase correcta. P(c) es la probabilidad a priori de que un documento pertenezca a la clase c. Si los términos de un documento no proporcionan una evidencia clara de una clase o categoría frente a otra, se elige la que tiene mayor probabilidad a priori (Manning, Raghavan y Schütze 2009, 258).
Supongamos que (t1, t2, ... tnd) son los tokens de d que forman parte del vocabulario que utilizamos para la clasificación y nd es el número de tokens en d. Por ejemplo, (t1, t2, ... tnd) para la oración Pekín y Taipéi se unen a la OMC puede ser (Pekín, Taipéi, unen, OMC), con nd = 4, si tratamos los términos y el artículo "el" como palabras vacías (Manning, Raghavan y Schütze 2009, 258).
De acuerdo con Manning, Raghavan y Schütze (2009, 258), "en la clasificación de textos, la finalidad es encontrar la mejor clase o categoría para un documento. La mejor clase en la clasificación NB es la clase más probable o máxima a posteriori (MAP) C_map, que está representada por la Fórmula 2".
"Se sustituye P por P^ porque no se conocen los verdaderos valores de los parámetros P(c) y P(tk ǀ c), sino que se estiman a partir del conjunto de entrenamiento" (Manning, Raghavan y Schütze 2009, 258).
Manning, Raghavan y Schütze (2009, 258) mencionan que en la ecuación anterior se multiplican muchas probabilidades condicionales, una para cada posición 1 ≤ k ≤ n_d. Esto puede dar lugar a un desbordamiento de punto flotante. Por lo tanto, es mejor realizar el cálculo sumando logaritmos en lugar de multiplicar las probabilidades. La clase con la mayor log de probabilidades sigue siendo la más probable; y la función del logaritmo es monótona. Por lo tanto, la maximización que realmente se hace en la mayoría de las implementaciones de NB se muestra en la Fórmula 3:
Cada parámetro condicional
De acuerdo con Manning, Raghavan y Schütze (2009, 259) "los parámetros
"Donde, Nc es el número de documentos de la clase c y N es el número total de documentos. Estimamos la probabilidad condicional
"Donde, Tct es el número de ocurrencias de t en los documentos de entrenamiento de c, incluyendo múltiples apariciones de un término en un documento. En este caso se realizó la suposición de independencia posicional, que describe lo siguiente: Tct es un recuento de ocurrencias en todas las posiciones k en los documentos del conjunto de entrenamiento" (Manning, Raghavan y Schütze 2009, 260).
Manning, Raghavan y Schütze (2009, 260) señalan que el problema de estas estimaciones radica en que el resultado es cero para una combinación de término-clase que no aparece en los datos de entrenamiento [...]. Para la eliminación de los ceros se utilizó el suavizado de Laplace, que simplemente añade uno a cada recuento, como se puede observar en la Fórmula 6:
"Donde, B = ǀVǀ es el número de términos del vocabulario. El alisado de adición puede interpretarse como una prioridad uniforme (cada término aparece una vez para cada clase) que se actualiza a medida que llegan las pruebas de los datos de entrenamiento" (Manning, Raghavan y Schütze 2009, 260).
Estructura
El algoritmo utilizado en este trabajo es el Naïve Bayes Multinomial descrito por Manning, Raghavan y Schütze (2009, 260). Consta de dos secciones, i) entrenamiento (Tabla 5), y ii) prueba (Tabla 6).
Tabla 5 Naïve Bayes Multinomial (Entrenamiento)
| Naïve Bayes Multinomial (Entrenamiento) (C,D) | |
|---|---|
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
Fuente. Adaptado de Manning et al. (2009, 260)
Tabla 6 Naïve Bayes Multinomial (Prueba)
| Naïve Bayes Multinomial (Prueba) (C, V, priori, prob, d) | |
|---|---|
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
Fuente: Adaptado de Manning et al. (2009, 260)
Presentación y análisis de resultados
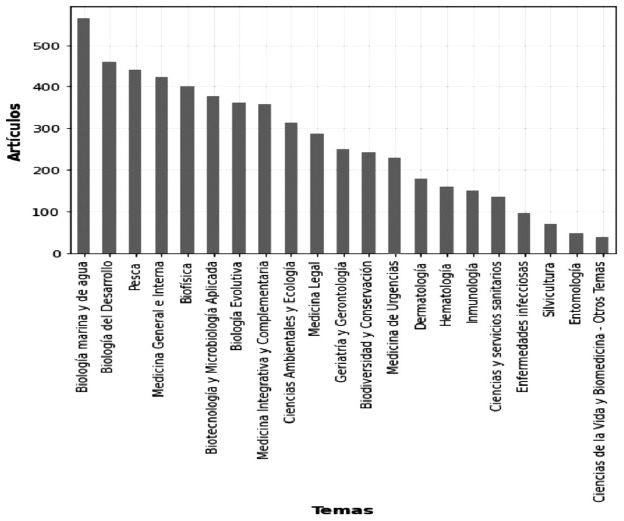
El desarrollo del algoritmo de clasificación requirió la utilización de dos conjuntos de datos (entrenamiento y prueba). Cada uno de los artículos de ambos conjuntos de datos ya tenían asignados temas de acuerdo con el área de investigación antes mencionada. En las Figuras 1 y 2 se presenta la distribución de los 21 temas que consideramos para el desarrollo del algoritmo.
Los temas de la Figura 1 representan datos de entrenamiento que permitieron que el algoritmo aprenda a predecir un tema determinado para cada artículo, con base en un cálculo probabilístico de la dispersión de palabras de los resúmenes. Los temas de la Figura 2 son elementos de referencia que sirven como apoyo para medir el rendimiento del algoritmo, realizando comparaciones entre los temas asignados originalmente por el WoS y los temas calculados automáticamente.
Para evaluar el rendimiento general del algoritmo utilizamos las siguientes métricas:
Exactitud (Accuracy). De acuerdo con Arjaria, Rathore y Cherian (2021, 319), "El cálculo de la exactitud se utiliza para comparar la eficiencia del modelo. Tiene en cuenta el número total de predicciones correctas realizadas por el algoritmo. Se calcula como se muestra en la Fórmula 7."
Exhaustividad (Recall). De acuerdo con Arjaria, Rathore y Cherian (2021, 319), "La exhaustividad se calcula tomando la proporción de entradas positivas correctamente identificadas como positivas. Se calcula como se muestra en la Fórmula 8."
Precisión (Precision). De acuerdo con Arjaria, Rathore y Cherian (2021, 319). "La precisión es el número de casos positivos predichos correctamente por el algoritmo. Se calcula como se muestra en la Fórmula 9."
Valor-F (F1 Score). De acuerdo con Arjaria, Rathore y Cherian (2021, 319), "Se define como una media ponderada de la precisión y la exhaustividad. Tiene su valor máximo en 1 y el peor en 0. Se calcula como se muestra en la Fórmula 10"
TP (Verdadero Positivo): Número de artículos que han sido correctamente clasificados.
TN (Verdadero Negativo): Número de artículos correctamente clasificados que no pertenecen realmente al tema asignado.
FP (Falso Positivo): Número de artículos clasificados erróneamente a un tema y que en realidad no es el tema que le corresponde.
FN (Falso Negativo): Número de artículos clasificados erróneamente a un tema, pero que en realidad los artículos sí corresponden a ese tema.
Tomando lo anterior como base, en la Tabla 7 se muestran los resultados del rendimiento del algoritmo, tras aplicarse en el corpus de prueba.
Tabla 7 Resultados del rendimiento del algoritmo
| Precisión | Exhaustividad | Valor-F | |
|---|---|---|---|
| Biodiversidad y Conservación | 0.98 | 0.38 | 0.54 |
| Biofísica | 0.95 | 0.95 | 0.95 |
| Biología Evolutiva | 0.83 | 0.93 | 0.88 |
| Biología del Desarrollo | 0.66 | 0.97 | 0.79 |
| Biología marina y de agua | 0.65 | 0.94 | 0.77 |
| Biotecnología y Microbiología Aplicada | 0.83 | 0.93 | 0.87 |
| Ciencias Ambientales y Ecología | 0.75 | 0.85 | 0.80 |
| Ciencias de la Vida y Biomedicina - Otros Temas | 0.00 | 0.00 | 0.00 |
| Ciencias y servicios sanitarios | 0.96 | 0.40 | 0.57 |
| Dermatología | 1.00 | 0.01 | 0.01 |
| Enfermedades infecciosas | 0.90 | 0.55 | 0.68 |
| Entomología | 0.00 | 0.00 | 0.00 |
| Geriatría y Gerontología | 0.93 | 0.80 | 0.86 |
| Hematología | 0.97 | 0.53 | 0.68 |
| Inmunología | 0.00 | 0.00 | 0.00 |
| Medicina General e Interna | 0.55 | 0.98 | 0.70 |
| Medicina Integrativa y Complementaria | 0.86 | 0.87 | 0.87 |
| Medicina Legal | 1.00 | 0.83 | 0.91 |
| Medicina de Urgencias | 0.91 | 0.74 | 0.82 |
| Pesca | 0.79 | 0.75 | 0.77 |
| Silvicultura | 1.00 | 0.27 | 0.43 |
| Exactitud | 0.77 | ||
| Desempeño promedio | 0.74 | 0.60 | 0.61 |
| Media ponderada | 0.78 | 0.77 | 0.73 |
En la Tabla 4 se observan los cálculos realizados de cada uno de los artículos correspondientes a los 21 temas en el área de investigación en Ciencias de la Vida y Biomedicina, utilizando las métricas Exactitud, Exhaustividad, Precisión y Valor-F.
Los temas que tuvieron una precisión superior al 90% son Biodiversidad y Conservación (98%); Biofísica (95%); Ciencias y servicios sanitarios (96%); Dermatología (100%); Enfermedades infecciosas (90%); Medicina de Urgencias (91%), y Silvicultura (100%). Estos resultados se debieron a la cantidad de datos de entrenamiento que utilizamos para estos temas. Los temas que menor precisión tuvieron contaban con pocos datos de entrenamiento, como Ciencias de la Vida y Biomedicina - Otros Temas; Entomología, e Inmunología.
La métrica de exhaustividad indica la capacidad del algoritmo para identificar la probabilidad de que un tema determinado corresponda a un artículo, "de esta forma se evalúa la eficacia del algoritmo sólo en un tema" (Sokolova, Nathalie y Stan 2006, 3). Biofísica clasifica el 95% de artículos correctamente; Biología el 93%, Biología del Desarrollo 97%, entre otros.
La exactitud, "es una métrica que evalúa la eficacia global de un modelo de clasificación" (Sokolova, Nathalie y Stan 2006, 3). En este caso, el algoritmo propuesto tuvo un porcentaje de 77% de eficiencia. Considerando la diversidad de idiomas en los corpus de artículos, la extensión del contenido de los resúmenes y su falta de normalización, entre otras circunstancias, podemos estimar que el porcentaje es satisfactorio en cuanto a la clasificación de temas automática.
El algoritmo propuesto puede ser utilizado como alternativa a los métodos tradicionales de clasificación de documentos, en un dominio de conocimiento particular, permitiendo crear servicios especializados orientados al desarrollo de sistemas computacionales para utilizarse en la gestión de información digital y electrónica.
Para representar de forma visual el rendimiento del algoritmo se generó una matriz de confusión. Los elementos diagonales representan resultados correctamente clasificados. Los resultados mal clasificados están representados fuera de las diagonales de la matriz. El mejor algoritmo tendrá una matriz de confusión con sólo elementos diagonales y el resto de los elementos a cero (Arjaria, Rathore, y Cherian 2021, 318).
En la Figura 3 se presenta la matriz de confusión del algoritmo propuesto.
En la Figura 3 se observa una matriz que contiene en los ejes "X" e "Y", los 21 temas en el área de Ciencias de la Vida y Biomedicina utilizados para desarrollar y evaluar el algoritmo. Los temas calculados representan aquellos que fueron generados automáticamente por el algoritmo, y los temas reales son los asignados originalmente por el Web of Science.
La matriz de confusión muestra que 16 de los 21 temas utilizados fueron clasificados correctamente, destacando los temas Medicina General e Interna; Biofísica; Biología Evolutiva; Biología del Desarrollo; Biología Marina y de Agua; Biotecnología y Microbiología Aplicada.
Discusión
La clasificación de documentos automática generalmente se asocia con las ciencias de la computación, abarcando diversos enfoques como: Análisis de sentimientos, clasificación de imágenes, clasificación de textos estructurados y no estructurados, entre otros. Estos enfoques permiten la implementación de algoritmos en distintas áreas de conocimiento.
Los estudios más recientes sobre la clasificación automática de documentos utilizan modelos basados en Transformes7, como se muestra en Lehecka et al. (2020); Cai et al. (2020); Yu, Su y Luo (2019), y Liu, Wang y Ren (2021), mostrando resultados favorables en la clasificación de documentos con múltiples etiquetas.
Se han desarrollado diversas investigaciones sobre clasificación de textos utilizando modelos probabilísticos, como el Multinomial de Naïve Bayes. En el trabajo de Gao, Zeng y Yao (2019) se analizó la construcción y el mejoramiento del modelo Naïve Bayes, para la clasificación de documentos. Otro estudio similar es el propuesto por Marikani y Shyamala (2020), el cual se enfoca en la clasificación de documentos sobre predicción de enfermedades cardiacas.
En el trabajo de Chen et al. (2019), se utilizó una modificación del algoritmo Naïve Bayes que facilita la correlación general entre distintas clases o categorías. En el trabajo de Harzevili y Alizadeh (2018) se utilizó un clasificador Mixto Bayes Ingenuo Multinomial Latente para relajar el supuesto de independencia dentro de la clasificación de documentos.
Dentro de la bibliotecología y ciencias de la información, algunos de los trabajos más destacados son los siguientes: Contreras (2016) presentó un clasificador automático para documentos, basado en el área Z del Sistema de Clasificación de la Biblioteca del Congreso (L.C), teniendo resultados favorables en la clasificación del material bibliográfico.
Kragelj, Matjaz, y Mirjana (2021) desarrollaron un modelo de clasificación automática de documentos antiguos, basado en el Sistema de Clasificación Decimal Universal (UDC). Como parte final, en el trabajo de Cassidy (2020) se utilizó el modelo Naïve Bayes para la clasificación de patentes, considerando códigos especializados para estos recursos.
Como se puede observar, los estudios sobre clasificación de documentos en el área de las ciencias de la información utilizando modelos probabilísticos no son muy frecuentes. Es por ello por lo que este trabajo intenta utilizar este modelo, como alternativa a los métodos tradicionales de clasificación de documentos y a otras herramientas implementadas dentro de este campo, que permita facilitar la recuperación de información bibliográfica en línea, a través de biblioteca digitales, repositorios o bases de datos bibliográficas.
Conclusiones y trabajos futuros
A través de la utilización del clasificador Naïve Bayes Multinomial, presentamos una experiencia en el desarrollo y prueba de un algoritmo que asigna automáticamente un tema a un documento basándose en un cálculo probabilístico de la dispersión de las palabras de los resúmenes.
El funcionamiento general del algoritmo analiza los resúmenes de un conjunto de registros bibliográficos codificados en tablas en formato CSV (Valores separados por comas), y con base en cálculos probabilísticos asigna un tema del área de investigación en Ciencias de la Vida y Biomedicina a cada uno de los artículos, añadiéndolos a otra columna de la tabla.
La exactitud del algoritmo para la asignación de temas correspondientes a Ciencias de la Vida y Biomedicina es de 77%. Representa un rendimiento apropiado para considerar su utilización dentro de las unidades y centros de información. Esto reflejará un proceso de incorporación de las tecnologías de información y de aprendizaje automático supervisado.
La utilización del algoritmo implica un proceso de entrenamiento con datos de prueba sobre un área de conocimiento específico; de este modo, se puede diversificar su uso en otras disciplinas, permitiendo crear servicios especializados orientados al desarrollo de sistemas computacionales para utilizarse en la gestión de información digital y electrónica.
Tras la aplicación del algoritmo, la razón de que algunos temas se asignaron de forma correcta, en la mayoría de los casos se debió a la cantidad de datos de entrenamiento que incluimos en esas áreas, ya que el clasificador logró comprender más sobre éstos, en comparación con los temas que tenían pocos datos de entrenamiento y, en su caso, la exactitud fue menor.
Como se mencionó anteriormente, el algoritmo asigna un tema a un documento con base en una distribución de las palabras de los resúmenes; de esta forma no afectaría de qué área del conocimiento se tratase, ni las brechas de idioma; sólo bastaría con establecer datos de entrenamiento suficientes para que el algoritmo tuviera un rendimiento similar o superior al presentado en este trabajo.
Utilizar este algoritmo no implica altos costos financieros, ya que se puede replicar en un entorno como Google Colaboratory, en el que se brindan recursos computacionales a través de sus servidores. De esta forma, el algoritmo propicia que el profesional de la información documental obtenga conocimientos y habilidades que le permitirán desarrollarse en la industria 4.0.
El algoritmo implementado en este trabajo puede servir como base para el desarrollo de nuevos métodos de clasificación automática de documentos dentro del área de bibliotecología y ciencias de la información, a partir de la utilización de grandes modelos de lenguaje basados en Transformes como BERT, GPT-3, etcétera, que aprovechen el aprendizaje profundo para minimizar la cantidad de datos de entrenamiento necesarios para el buen funcionamiento de un algoritmo de clasificación.
Estos métodos pre-entrenados pretenden ejercer un cambio de paradigma en los modelos de aprendizaje supervisado, modificándolos a aprendizaje auto-supervisado. De este modo, el rendimiento de estos algoritmos de clasificación puede ser indistinguible en comparación con la misma tarea realizada por un profesional de la información documental.
Como se mencionó anteriormente, uno de los objetivos principales de este trabajo es presentar una experiencia en el desarrollo de un algoritmo de clasificación, con la finalidad de promover este tipo de investigaciones dentro de nuestro gremio, para que se pueda no sólo desarrollar este tipo de algoritmos de clasificación, sino aprovecharse para el desarrollo de modelos inteligentes de creación de resúmenes automáticos, extracción de palabras clave, identificación y extracción automática de metadatos, implementación de chatbots, sistemas de recomendación, desarrollo de ontologías, implementación de análisis de satisfacción de los usuarios, o la creación de motores de búsqueda de última generación.











 nueva página del texto (beta)
nueva página del texto (beta)