Artículos

 

Evaluación de la flexibilidad elástica de sistemas de piso utilizados en edificios urbanos*

 

Arturo Tena Colunga¹, Karen Lineth Chinchilla Portillo² y Gelacio Juárez Luna^3,1

 

¹ Profesor, Departamento de Materiales, Universidad Autónoma Metropolitana Azcapotzalco, Av. San Pablo 180, Col. Reynosa Tamaulipas, 02200 México, DF, e-mail: atc@correo.azc.uam.mx.

² Posgrado de Ingeniería Estructural, Universidad Autónoma Metropolitana Azcapotzalco, Av. San Pablo # 180, 02200, México, DF, e-mail klchinchilla@gmail.com.

³ Profesor Departamento de Materiales, Universidad Autónoma Metropolitana Azcapotzalco, Av. San Pablo 180, Col. Reynosa Tamaulipas, 02200 México, DF, e-mail: gjl@correo.azc.uam.mx.

 

Artículo recibido el 3 de mayo de 2013.
Aprobado para su publicación el 16 de octubre de 2013.

 

Resumen

Se presenta un estudio analítico en el intervalo elástico lineal, que evalúa el comportamiento de diafragma de los sistemas de piso más ampliamente utilizados en edificación urbana en México: losa perimetralmente apoyada, vigueta y bovedilla, losacero y losa reticular aligerada con casetones de fibra de vidrio o bloques de espuma de poliestireno, así como su clasificación de acuerdo a criterios basados en desplazamientos y fuerzas. En la investigación se consideraron dos factores identificados en estudios previos que favorecen la potencial flexibilidad del diafragma: a) la relación de aspecto de la planta del edificio y, b) la rigidez del sistema de piso.

Para evaluar la potencial condición de flexibilidad de diafragma de los sistemas de piso, para cada sistema de piso y relación de aspecto de la planta en estudio, se realizaron análisis elásticos ante carga lateral uniformemente distribuida en el sistema de piso en modelos detallados de elementos finitos empleando el programa Ansys. La condición de diafragma se evaluó por medio de los siguientes parámetros: (a) los perfiles de los desplazamientos laterales (Δ) obtenidos en el último nivel de los distintos sistemas de piso en estudio, normalizados con respecto a los desplazamientos en ese mismo nivel de los modelos donde el diafragma es infinitamente rígido (Δ_RÍGIDO) y, (b) el factor de amplificación del cortante basal de los marcos centrales con respecto a los marcos del perímetro. Se evaluaron también dos índices de flexibilidad (rigidez) propuestos en la literatura: a) el índice propuesto en normas de los Estados Unidos como el UBC-97, ASCE-7 y FEMA-368 y, b) el índice R propuesto por Ju y Lin en 1999. A partir de los resultados del extenso estudio paramétrico descrito, se puede concluir que un sistema de piso diseñado conforme a los reglamentos y las recomendaciones de diseño de los fabricantes, más la experiencia de prestigiados ingenieros de la práctica, puede liderar a sistemas de piso que se comporten razonablemente como diafragmas rígidos para claros que no sean muy grandes (6 metros o menos), normalmente utilizados en edificios para vivienda. Sin embargo, esta observación no se puede generalizar, pues otras prácticas de diseño favorecen la presencia de diafragmas semi-rígidos, semi-flexibles o claramente flexibles, principalmente para los claros (10 metros o más) usados en edificios para oficinas.

Palabras clave: diafragma rígido, diafragma flexible, sistemas de piso, irregularidad estructural, análisis elásticos.

 

Abstract

A study devoted to define the diaphragm condition using linear-elastic analyses for structures with the most widely used floor systems in Mexico (two-way ribbed RC slabs, beam and block, steel decks and waffle RC flat slabs is presented. The models were analyzed under lateral loading. Previously proposed force and displacement criteria were used to assess their behavior as diaphragm. Two variables that favor the potential flexibility of the diaphragm were assessed in the research: a) the plan aspect ratio of buildings and, b) the stiffness of the floor system.

Different plan aspect ratios for the buildings were considered in the study. All models were analyzed under uniformly distributed lateral loading with Ansys finite element software using refined meshes. In order to assess the behavior of the different floor systems as a diaphragm, force and displacement criteria were used. The diaphragm condition was assessed using the following parameters: (a) profiles of lateral displacements (Δ) obtained in the top level of the studied floor systems normalized with respect to the lateral displacements at the same level for a rigid diaphragm model (Δrigid) and, (b) the amplification factor for the base shear of central frames with respect to perimeter frames. ASCE-7 and Ju and Lin (1999) flexibility indexes were evaluated in the study. Based upon the results of the described parametric study, it can be concluded that a floor system designed according to building codes and the recommendations of manufacturers, plus the experience of prestigious practicing engineers, could lead to floor systems that behave reasonably as rigid diaphragms when the floor spans are not very large (6 meters or less), commonly used in apartment buildings. However, this observation cannot be generalized, because other design practices may favor the presence of semi-rigid, semi-flexible or flexible diaphragms, particularly for floor spans of 10 meters or more, frequently used in office buildings.

Keywords: Rigid diaphragm, flexible diaphragm, floor systems, structural irregularities, elastic analyses.

 

INTRODUCCIÓN

Actualmente existe una extensa variedad de opciones estructurales para dar solución a los sistemas de piso empleados en edificios, lo que obedece a que las tecnologías constructivas buscan satisfacer, en primera instancia, las necesidades de una industria de la edificación más eficiente, rápida y económica. Muchas de estas soluciones estructurales se han desarrollado para satisfacer la función primaria de un sistema de piso, que es resistir y distribuir de manera eficiente las cargas verticales en la estructura. Sin embargo, su extensión y aplicación a cargas accidentales como sismo o viento no debe extrapolarse directamente sin hacer un análisis adecuado de cómo estos sistemas de piso resisten y distribuyen las cargas laterales. El dar por un hecho que componen diafragmas rígidos y resistentes sin ningún tipo de estudio (analítico y/o experimental) puede comprometer seriamente la integridad de la estructura ante acciones accidentales de importancia.

Existen estudios tanto experimentales (Karadogan et al. 1980, Nakashima et al. 1984, López et al. 2001, Pinho et al. 2008) como analíticos (Saffarini y Qudaimat 1992, De la Colina 1999, León 2007, Tena y Cortés 2009), que han demostrado que las losas perimetralmente apoyadas, las losas planas de concreto reforzado y la vigueta y bovedilla constituyen diafragmas razonablemente rígidos y resistentes ante carga lateral para relaciones de aspecto de planta menores o iguales a 2.0 y para espesores comunes según demanda su diseño ante cargas verticales, dado que estos sistemas de piso transfieren y resisten razonablemente movimientos de cuerpo rígido sin experimentar deformaciones relativas de importancia.

Sin embargo, para relaciones de aspecto mayores a 2.0, el diafragma ya deja de ser suficientemente rígido y su flexibilidad no debería despreciarse (Panahshahi et al. 1991, Kunnath et al. 1991, Saffarini y Qudaimat 1992, Ju y Lin 1999, Doudoumis y Athanatopoulou 2001, Barron y Hueste 2004, Bal y Ozdemir 2006, Al Harash et al. 2008, Moeini y Rafezy 2011). En contraste, no se puede afirmar la condición de diafragma rígido para distintas relaciones de aspecto o espesores relativamente reducidos de lo que se conoce como "firme de compresión" para otros sistemas que ya tienen un tiempo razonable de uso en el mercado mexicano, como la losa plana reticular aligerada (Chen 1986, Chen et al. 1988, Rodríguez et al. 1995), la vigueta y bovedilla (Damian et al. 2000), la losacero (Sarkissian et al. 2006), sobre todo si no cuenta con un "firme de compresión" (Paulte et al. 2004, Mastrogiuseppe et al. 2008), o los nuevos sistemas que están teniendo una gran demanda en estos días, como las losas planas aligeradas con bloques de espuma de poliestireno de grandes dimensiones (de un metro por un metro, incluso más largos), situación que puede conducir a una reducción importante de su rigidez y resistencia ante cargas laterales.

Las configuraciones irregulares en planta (Ju y Lin 1999, López y Raven 1999, Doudoumis y Athanatopoulou 2001, Moeini y Rafezy 2011) y la presencia de aberturas importantes en los sistemas de piso (Doudoumis y Athanatopoulou 2001, Al Harash et al. 2008, Óztürk 2011) también favorecen el desarrollo de la flexibilidad de los diafragmas.

Los estudios reportados en la literatura especializada han enseñado que la respuesta de estructuras con diafragmas flexibles difiere mucho de aquéllas con diafragmas rígidos, sobre todo ante cargas sísmicas (por ejemplo, Celebi et al. 1989, Panahshahi et al. 1991, Kunnath et al. 1991, Tena-Colunga 1992, Tena-Colunga y Abrams 1992 y 1996, Ju y Lin 1999, De la Colina 1999, Fleischman y Farrow 2001, Doudoumis y Athanatopoulou 2001, Fleischman et al. 2002, Basu y Jain 2004, Barron y Hueste 2004, Cohen et al. 2004, Kim y White 2004, Bal y Ozdemir 2006, Al Harash et al. 2008, Langroudi et al. 2011).

Si se tienen dos estructuras idénticas en planta y cuyos elementos resistentes verticales (marcos, muros, contravientos, etc.) son idénticos también, pero en una el sistema de piso se comporta como diafragma rígido y en la otra como diafragma flexible, se observarán, entre otras, las siguientes diferencias importantes en su comportamiento dinámico ante cargas laterales:

(a) los periodos de vibración de la estructura con diafragmas flexibles serán mayores a la de la estructura con diafragmas rígidos (Kunnath et al. 1991, Tena-Colunga y Abrams 1992 y 1996, Tremblay y Stiemer 1996, Barron y Hueste 2004, Paultre et al. 2004, Lee et al. 2007, Mastrogiuseppe et al. 2008, Langroudi et al. 2011, Sadashiva et al. 2012). Dependiendo del tipo de suelo donde se ubiquen las estructuras de interés, el alargamiento del periodo podrá conducir a la estructura con diafragmas flexibles a mayores demandas de aceleración (rama ascendente del espectro) o a menores demandas de aceleración (rama descendente del espectro) con respecto a la estructura con diafragmas rígidos.

(b) los modos de vibración en traslación lateral de la estructura con diafragmas flexibles serán dominados por las deformaciones de los diafragmas (conocida como "acción de diafragma" en la literatura técnica), mientras que en la estructura con diafragmas rígidos serán dominados por las deformaciones de los elementos resistentes verticales. Esto normalmente conduce a que en la dirección donde se considera que actúa la excitación sísmica, en las estructuras con diafragmas flexibles se tenga una distribución no uniforme de aceleraciones y desplazamientos entre los elementos resistentes ante carga lateral en un nivel dado (Celebi et al. 1989, Kunnath et al. 1991, Tena-Colunga 1992, Tena-Colunga y Abrams 1992 y 1996, Fleischman et al. 2002, Cohen et al. 2004, Kim y White 2004, Óztürk 2011, Sadashiva et al. 2012). De hecho, las aceleraciones y desplazamientos laterales son notablemente mayores en los sistemas de piso, principalmente al centro de su claro (Celebi et al. 1989, Tena-Colunga 1992, Tena-Colunga y Abrams 1992 y 1995, Cohen et al. 2004), y dinámicamente en los elementos resistentes verticales más flexibles, por lo que las fuerzas sísmicas que se demandan a estos elementos son notablemente mayores que las de los elementos resistentes verticales más rígidos (Tena-Colunga y Abrams 1992 y 1995, Kim y White 2004). Lo anterior es contrario a lo que sucede en una estructura con diafragmas rígidos, donde los desplazamientos y aceleraciones laterales son iguales para todos los elementos resistentes verticales y, por ello, las fuerzas laterales se distribuyen en proporción a su rigidez lateral, por lo que los elementos verticales más rígidos atraen una mayor proporción de las fuerzas sísmicas.

(c) en la dirección perpendicular a la cual se considera que actúa la excitación sísmica, en las estructuras con diafragmas flexibles, los sistemas de piso imponen deformaciones fuera del plano muy importantes a las vigas de perímetro (Kolston y Buchanan 1980, Naeim y Boppana 2001) y a los elementos verticales resistentes en la dirección ortogonal (Tena-Colunga y Abrams 1992, 1995 y 1996, Kim y White 2004), que en muchas ocasiones originan su falla (por ejemplo, en el caso de muros de mampostería) o agrietamientos muy importantes (por ejemplo, en el caso de vigas y muros de concreto reforzado), como se ha observado y constatado en varios sismos anteriores, por ejemplo, en los sismos de Umbria-Mache en Italia en 1977 (Brignola et al. 2008) o de Loma Prieta en 1989 y de Northridge en 1994 (Tena 2010).

(d) si existen asimetrías importantes en rigideces y/o masas, la estructura con diafragmas rígidos experimentará un acoplamiento modal importante y será sujeto de movimientos torsionales de importancia. En cambio, en la estructura con diafragmas flexibles los efectos de torsión serán generalmente reducidos (Tena-Colunga y Abrams 1996, De la Colina 1999, Óztürk 2011). Este constituye uno de los aspectos benéficos de la flexibilidad de diafragma: reduce el acoplamiento por torsión.

En virtud de todo lo expuesto anteriormente, se puede afirmar que la flexibilidad en el sistema de piso varía significativamente el comportamiento dinámico de las estructuras, razón por la cual no es apropiado bajo ningún motivo suponer que es seguro y conservador diseñar ante sismo a estructuras con diafragmas flexibles con herramientas e hipótesis comúnmente empleadas en estructuras con diafragmas rígidos.

Por ello, en este estudio se evalúa, en el intervalo de comportamiento elástico lineal, qué tipo de diafragma constituyen los sistemas de piso más empleados en edificación urbana en México: losa perimetralmente apoyada, vigueta y bovedilla, losacero y losa reticular aligerada con casetones de fibra de vidrio o bloques de espuma de poliestireno. Los detalles del estudio se presentan en Chinchilla (2012) y en las siguientes secciones se presentan y discuten los aspectos más relevantes del estudio.

 

MODELOS EN ESTUDIO

Con la finalidad de evaluar la condición de diafragma de los sistemas de piso más empleados en la edificación urbana más comúnmente construida en México, se diseñaron, como se describe después, modelos tipo de edificios con base en marcos, los cuales se dividieron en dos grupos, uno enfocado a viviendas, y el otro a oficinas.

Para los edificios para vivienda se consideraron claros de seis metros en ambas direcciones, que es una dimensión típicamente empleada en edificios de departamento de interés medio, e incluso algunos de interés social. Para estos modelos se consideraron los siguientes sistemas de piso (figura 1):

• Losa perimetralmente apoyada, la cual fue diseñada conforme a las Normas Técnicas Complementarias para Diseño de Estructuras de Concreto vigentes (NTCC-04 2004).

• Vigueta y bovedilla, diseñada según manual PREMEX (2011).

• Losa plana reticular con casetones de 40x40 cm, diseñada según la práctica de diseño del despacho García-Jarque Ingenieros (García Jarque 2011) que emplea el método de los coeficientes establecido en las NTCC-04 (2004) para determinar los momentos de diseño en las nervaduras.

Para los edificios para oficinas se consideraron claros de quince metros en su dirección larga, y diez metros en la dirección corta, dimensiones que cubren razonablemente los claros manejados hoy en día en edificios importantes que se construyen en la ciudad de México. Los sistemas de piso considerados fueron los siguientes (figura 2):

• Losa perimetralmente apoyada, diseñada según NTCC-04 (2004).

• Losacero, diseñada con apoyo del manual de Industrias Monterrey (IMSA 2011), según la práctica del despacho García-Jarque, que se basa en aplicar los criterios de la reglamentación del Instituto Americano de la Construcción en Acero (AISC, por sus siglas en inglés) y a las recomendaciones de la Sociedad Americana de Ingenieros Civiles (ASCE, por sus siglas en inglés) en cuanto a construcción compuesta.

• Losa reticular con casetones de 100 x 100 cm, diseñada según la práctica de diseño del despacho García-Jarque Ingenieros (García Jarque 2011) que emplea el método de los coeficientes establecido en las NTCC-04 (2004) para determinar los momentos de diseño en las nervaduras.

Para cada uno de los dos grupos de modelos conformados se hizo variar su relación de aspecto en planta, con el propósito de evaluar su comportamiento como diafragma a medida que la planta va siendo más alargada. En el grupo de edificios para vivienda las relaciones de aspecto en planta estudiadas fueron 1.0 (ya sea con dos o tres tableros por lado), 1.5, 2.0, 2.5, 3.0, 3.5 y 4.0, como se ilustra en la figura 3.

Para el grupo de edificios para oficinas, las relaciones de aspecto en planta estudiadas fueron 1.0, 1.5, 2.25, 3.0, 3.75 y 4.5, como se ilustra en la figura 4.

Cabe señalar que el intervalo de las relaciones de aspecto en planta estudiadas, tanto para edificios para vivienda como para oficinas, rebasa el límite de 2.5 establecido en las normas de diseño por sismo de México (NTCS-04 2004, MOC-2008 2009) para definir a una estructura como regular por este concepto.

Diseño de los distintos sistemas de piso

Cada uno de los sistemas de piso se diseñó principalmente ante cargas verticales considerando su peso propio, sobrecargas, cargas vivas, factores de carga y combinaciones de carga conforme al Reglamento de Construcciones para el Distrito Federal (RCDF-04 2004), así como la revisión de estados límites de deformación, como se describe con detalle en Chinchilla (2012).

Para el diseño de los sistemas de piso con base en losas perimetralmente apoyadas, se establecieron las siguientes dimensiones de los tableros: a) 6m por 3m para vivienda y, b) 5m por 5m para oficina. Nótese que para que se puedan formar estos tableros, el sistema de piso en vivienda se apoya en una viga secundaria a lo largo del tablero y, para oficinas se apoya en una viga secundaria a lo largo del tablero y en dos vigas secundarias a lo ancho del mismo, como se ilustra en la figura 5.

Las losas perimetralmente apoyadas fueron diseñadas conforme al método de los coeficientes de las NTCC-04 (2004). Los detalles del diseño se presentan en Chinchilla (2012) y se puede resumir que se requirió un espesor h=11 cm para los edificios para vivienda y h=12 cm para los edificios para oficinas, suponiendo que las propiedades de diseño para el concreto eran f_c'=250 kg/cm² y E_c=221,359 kg/cm² y para el acero de refuerzo f_y=4,200 kg/cm² y E_s=2x10⁶ kg/cm². Las vigas secundarias se diseñaron para satisfacer los estados límites de resistencia y deformación, empleando un modelo tridimensional en el programa Sap-2000 (CSI 2005), suponiendo las mismas propiedades para el concreto y el acero de refuerzo, como también se describe en Chinchilla (2012).

Para el diseño del sistema de piso con base en vigueta y bovedilla, se empleó el manual técnico de la empresa Premezclados Mexicanos (PREMEX 2011), el cual toma en cuenta que este sistema de piso trabaja en una sola dirección. Su sistema de piso se compone de viguetas de concreto pretensado f_c'=400 kg/cm² y E_c=280,000 kg/cm²), bovedilla de arena-cemento (f_c'=275 kg/cm² y E_c=232,163 kg/cm²) y un firme de concreto hecho en obra (/"_c=250 kg/cm² y E_c=221,359 kg/cm²), cuya función es integrarse en forma monolítica con la vigueta y la bovedilla, y cuyo espesor depende de la bovedilla a utilizar. Conforme se describe en Chinchilla (2012), el diseño del sistema de piso para vivienda con base en vigueta y bovedilla requirió viguetas y bovedillas de 16 cm de peralte (figura 6) y un firme de compresión de 4 cm, por lo que espesor total de este sistema de piso resultó h=20 cm.

El diseño de las losas reticulares aligeradas con bloques de espuma de poliestireno (o sin ellos) se hizo utilizando el método de los coeficientes propuesto en las NTCC-04 (2004), con el apoyo de una hoja de Excel programada y desarrollada por el despacho García Jarque Ingenieros. Para los edificios de vivienda se consideraron dimensiones de los bloques (o casetones) de 40 cm x 40 cm, mientras que para los edificios para oficinas se consideraron bloques o casetones de 100 cm x 100 cm. Se supuso que las propiedades de diseño para el concreto eran f_c'=250 kg/cm² y E_c=221,359 kg/cm² y para el acero de refuerzo f_Y=4,200 kg/cm² y E_s=2x10⁶ kg/cm². Los detalles del diseño se presentan en Chinchilla (2012), pero se puede resumir que para los edificios para vivienda se requirió de una losa con peralte total h=30 cm, un espesor del firme de concreto t=5 cm y ancho de nervaduras b=15 cm, mientras que para los edificios para oficinas se obtuvo una losa con peralte total h=45 cm, un espesor del firme de concreto t=7 cm y ancho de nervaduras b=15 cm.

El diseño de la losacero se realizó conforme a una hoja de Excel desarrollada también por el despacho García Jarque Ingenieros, la cual fue programada de acuerdo a la reglamentación del AISC y a las recomendaciones de la ASCE en cuanto a construcción compuesta. Esta hoja automatiza el cálculo del momento resistente, según la ubicación del eje neutro, y posteriormente el cálculo de la deflexión del sistema, para poder ser comparados contra el momento actuante en el sistema y la deflexión permitida, ambos calculados según las exigencias del RCDF-04 (2004).

Tomando en cuenta las recomendaciones del Ing. Francisco García Jarque, se consideró que la lámina de acero está apoyada cada 2.0 metros en las vigas secundarias con base en perfiles I de acero estructural. Cabe señalar que el calibre de la lámina de acero a emplear es función del espaciamiento de las vigas secundarias, del espesor del firme de concreto y del número de apoyos, según las recomendaciones del fabricante (IMSA 2011). El diseño final conforme al manual del fabricante IMSA requirió entonces de una lámina de acero Sección 4 calibre 22 (figura 7) con una capa de compresión de concreto de 6 cm (f_c'=200 kg/cm² y E_c=173,925 kg/cm²) montada sobre vigas secundarias de acero perfil W18x86 separadas cada 2 m. Las propiedades del acero del perfil y de la lámina son f_Y=2,530 kg/cm² y E_s=2x10⁶ kg/cm². El diseño de la losacero fue revisado con el programa "Vigas compuestas y vibraciones" (Cincúnegui 2011), y se observó coincidencia con los resultados obtenidos con la hoja de cálculo empleada en el diseño.

Diseño de los marcos de los edificios en estudio

Por simplicidad, los distintos modelos de edificios se diseñaron para tres pisos con altura típica de entrepiso h=3.5 m, dado que en este estudio inicial la condición de diafragma se evaluó, como se describe adelante, con modelos tridimensionales de elementos finitos ante carga lateral estática.

Con la finalidad de tener un marco de referencia común para los distintos sistemas de piso en estudio, se decidió diseñar todos los edificios con base en marcos dúctiles de concreto reforzado, aunque se reconoce que el uso del sistema de piso de losacero es poco común en marcos de concreto reforzado, pero si se utiliza en construcción compuesta acero-concreto reforzado.

Para facilitar también la comparación de los resultados entre las distintas relaciones de aspecto en estudio, se propuso de inicio hacer dos diseños tipo de los edificios para cada tipo de edificio (vivienda y oficina). Los diseños tipo considerados se describen a continuación:

• Diseño Tipo I: Las secciones de las vigas y las columnas de los marcos se obtuvieron con base en el diseño de un edificio compuesto por marcos de tres crujías en dirección x, y marcos de dos crujías en dirección y.

• Diseño Tipo II: Las secciones de las vigas y las columnas de los marcos se obtuvieron con base en el diseño de un edificio compuesto por marcos de cinco crujías en dirección x, y marcos de dos crujías en dirección y.

La división de los edificios tipo propuesta inicialmente conforme a las relaciones de aspecto en planta en estudio se reportan en la tabla 1.

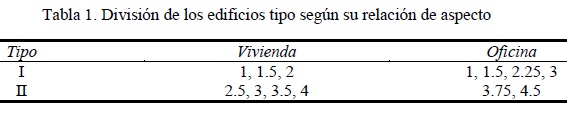
Dado que el sistema de piso que normalmente se toma como referencia como "diafragma rígido" es el compuesto por losas de concreto reforzado perimetralmente apoyadas, los marcos tipo que componen a cada estructura fueron diseñados para soportar la carga que produce el sistema de piso perimetralmente apoyado. Se decidió hacerlo de esta manera para asegurar que se tenga un marco de referencia común en todos los sistemas de piso en estudio para el contraste de la rigidez lateral que aporta el marco con respecto al sistema de piso y, por ende, ésta no sea una variable que complique la comparación de la condición de diafragma entre los distintos sistemas de piso en estudio.

Los marcos de los edificios se diseñaron tomando en cuenta combinaciones de cargas gravitacionales y laterales asociadas a un diseño conforme al RCDF-04. El análisis por sismo se hizo conforme al método estático y suponiendo un cortante basal de diseño V/W=c/Q'=0.05. Las propiedades de diseño supuestas para el concreto fueron f_c'=250 kg/cm² y E_c=221,359 kg/cm² y para el acero de refuerzo f_y=4,200 kg/cm² y E_s=2x10⁶ kg/cm².

Los detalles del diseño de vigas y columnas conforme al Reglamento de Construcciones del Distrito Federal (RCDF-04 2004) y sus Normas Técnicas Complementarias correspondientes (NTCC-04 2004) se presentan en Chinchilla (2012). Del proceso de diseño se obtuvo que, para fines prácticos, las dimensiones y los refuerzos de las secciones transversales para los edificios tipo I y II pudieran ser las mismas, por lo que los diseños de las vigas y columnas se resumen en las tablas 2 y 3 respectivamente. La notable diferencia entre las secciones obtenidas para edificios de vivienda y oficina se debe principalmente a la dificultad de cumplir estados límites de deformación y de resistencia para los grandes claros de los edificios de oficina y a que las cargas vivas y muertas en oficinas son mayores.

 

MODELADO CON ELEMENTOS FINITOS

Generalidades

Para evaluar la potencial condición de flexibilidad de diafragma de los sistemas de piso en estudio, se realizaron análisis elásticos ante carga lateral uniformemente distribuida en el sistema de piso, para lo cual se construyeron modelos de elementos finitos empleando para ello el programa Ansys (Ansys 2009), como se reporta con profundidad en Chinchilla (2012). Dada la complejidad de los modelos, se revisó cuidadosamente que en el mallado utilizado se garantizara la continuidad de la estructura.

El tipo de elemento que se utilizó en el modelado de vigas, columnas y sistemas de piso es un sólido (Solid-186 de la librería de Ansys) con formulación isoparamétrica, que dispone de 20 nudos y tres grados de libertad por nudo (desplazamiento en x, desplazamiento en y, desplazamiento en z), dado que se realizó una discretización fina y tridimensional de cada elemento, por lo que las rotaciones que experimentan son aproximadas por los campos de desplazamientos considerados. Además, con este elemento se pueden modelar comportamientos isotrópicos y ortotrópicos.

Las condiciones de apoyo en la base de los edificios fueron representadas como empotradas, restringiendo todos los desplazamientos en los nodos de las columnas adyacentes a la base.

Modelos con losas perimetralmente apoyadas

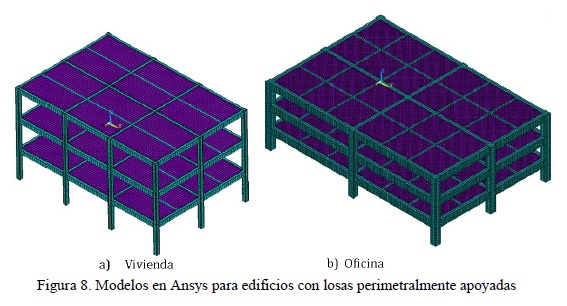
El modelado de este sistema de piso fue el más simple de todos, dado que es razonable suponer, por simplicidad, que sus propiedades en sus tres direcciones ortogonales principales son las mismas. Por lo tanto, con los elementos sólidos se representaron las mismas dimensiones de las secciones transversales obtenidas en el diseño para las losas (espesores) vigas (peralte y ancho) y columnas (ancho y largo) bajo una formulación isotrópica. Para los edificios para vivienda (por ejemplo, figura 8a) se requirió de una malla de 17,496 elementos sólidos para representar al modelo con relación de aspecto de la planta de 1.0 y de 57,669 para el de relación de aspecto de 4.0. Para los edificios para oficinas (por ejemplo, figura 8b) se requirió de una malla de 140,676 elementos sólidos para representar al modelo con relación de aspecto de la planta de 1.0 y de 276,420 para el modelo con relación de aspecto de 4.5.

Modelos con losas planas reticulares aligeradas

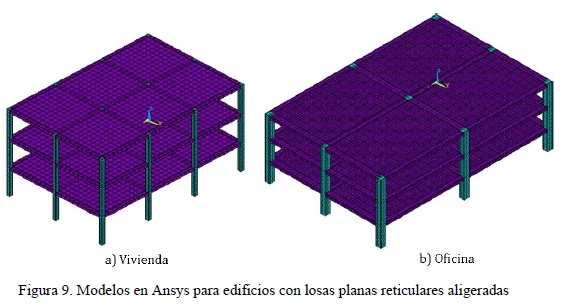
Como actualmente en este sistema se utilizan casetones (figura 2c) o en su defecto bloques de espuma de poliestireno (figura 1b), y dado que el módulo de elasticidad del bloque de espuma de poliestireno es muy bajo con respecto al del concreto (menor al 0.005%), para fines prácticos, no se modeló la rigidez de los bloques de espuma de poliestireno. Por lo tanto, la complejidad en este caso consistió en modelar con exactitud, empleando los elementos sólidos, las nervaduras, las zonas de casetones (sólo el firme de concreto) y las zonas macizas conforme al diseño del sistema de piso. Por lo tanto, con los elementos sólidos se representaron las mismas dimensiones de las secciones transversales obtenidas en el diseño para las losas (espesores), nervaduras (peralte y ancho), zonas de capiteles (ancho y peralte), vigas principales (peralte y ancho) y columnas (ancho y largo) bajo una formulación isotrópica. Para los edificios para vivienda (por ejemplo, figura 9a) se requirió de una malla de 18,846 elementos sólidos para representar al modelo con relación de aspecto de la planta de 1.0 y de 67,590 para el de relación de aspecto de 4.0. Para los edificios para oficinas (por ejemplo, figura 9b) se requirió de una malla de 111,528 elementos sólidos para representar al modelo con relación de aspecto de la planta de 1.0 y de 214,092 para la relación de aspecto de 4.5.

Modelos con vigueta y bovedilla

El modelado elaborado para este sistema, uno de los más complejos, fue el siguiente. Para representar a las vigas y columnas de los marcos se utilizó el modelado isotrópico descrito con anterioridad. Sin embargo, dadas las características de este sistema de piso donde: (a) se deben modelar por separado las viguetas (sólidas y rígidas, figura 6a) y las bovedillas (huecas y no tan rígidas, figura 6b), (b) hay diferencias geométricas importantes de las viguetas y bovedillas en sus direcciones principales (figura 6), que ocasionan que sus propiedades en la dirección paralela a las viguetas sean distintas a la dirección perpendicular a ellas (figura 10) y, (c) la diferencias existentes entre los módulos de elasticidad y de cortante de la vigueta , bovedilla y firme de compresión; se optó por utilizar un modelado ortotrópico en el elemento sólido que permite Ansys (2009) para representar al sistema de piso de vigueta y bovedilla, como se describe con detalle en Chinchilla (2012).

En Ansys se permite modelar la ortotropía a través de la definición de los módulos de elasticidad (E_X,E_Y,E_Z), de cortante (G_XY,G_YZ,G_XZ) y relaciones de Poisson (V_XY,V_YZ,V_XZ) en cada una de las direcciones ortogonales principales. En la figura 11 se identifica la ubicación de estos parámetros para constituir el modelado ortotrópico. Además, con la finalidad de simplificar un poco la definición del mallado, fue necesario transformar a las secciones "reales" (figuras 6a y 6b) por secciones sólidas prismáticas equivalentes (paralelepípedos regulares), empleando los principios de la sección transformada tanto a flexión como a cortante, como se ilustra en la figura 12, teniendo cuidado de mantener el comportamiento del sistema de piso después de la transformación, conforme se explica e ilustra con detalle en Chinchilla (2012). También cabe señalar que, conforme lo hacen los ingenieros que entienden que este sistema de piso trabaja principalmente en una dirección y que, en zonas sísmicas se deben balancear las rigideces del sistema de piso en las dos direcciones ortogonales, entonces se consideró en el modelado que la distribución de viguetas y bovedillas en los tableros se alterna conforme a un tablero de ajedrez (figura 11). Para los edificios para vivienda se requirió de una malla de 15,525 elementos sólidos para representar al modelo con relación de aspecto de la planta de 1.0 y de 55,269 para el modelo con relación de aspecto de 4.0.

Modelos con losacero

El modelado de la losacero fue muy parecido al descrito para el sistema de piso con vigueta y bovedilla, dado que conceptualmente trabajan de manera similar. Por lo tanto, para representar a las vigas y columnas de los marcos se utilizó el mismo modelado isotrópico. Dadas las características de este sistema de piso: (a) se deben modelar por separado la zona donde la lámina acanalada es más profunda y, por ello, el espesor del concreto por encima de ella es mayor con respecto a la zona donde la lámina acanalada sólo recibe al firme de concreto (figura 7), (b) hay diferencias geométricas importantes de la losacero en sus direcciones principales (figura 7), que ocasionan que sus propiedades en la dirección paralela al acanalamiento sean distintas a la dirección perpendicular a él (figura 13) y, (c) la diferencias existentes entre los módulos de elasticidad y de cortante de la lámina de acero y el concreto que se cuela en ella; se optó por utilizar un modelado ortotrópico en el elemento sólido que permite Ansys (2009) para representar al sistema de piso de losacero, como se describe con detalle en Chinchilla (2012).

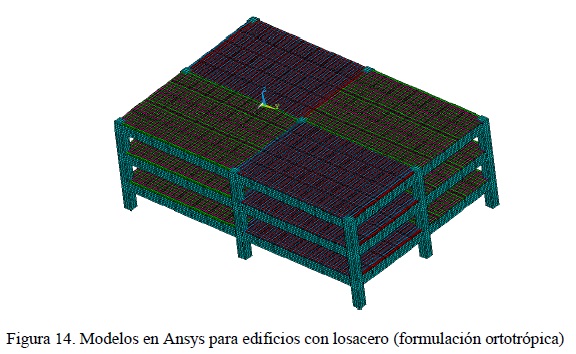
Además, con la finalidad de simplificar un poco la definición del mallado, fue necesario también hacer transformaciones para obtener secciones sólidas prismáticas equivalentes (paralelepípedos regulares, figura 12) a partir de las secciones trapezoidales "reales" (figura 7), empleando los principios de la sección transformada, teniendo cuidado de mantener el comportamiento del sistema de piso después de la transformación, conforme se presenta con detalle en Chinchilla (2012). También se consideró en el modelado que la distribución de la losacero en los tableros se alterna conforme a un tablero de ajedrez (figura 14), por las mismas razones que se hizo en la vigueta y bovedilla. Para los edificios de oficinas se requirió de una malla de 186,720 elementos sólidos para representar al modelo con relación de aspecto de la planta de 1.0 y de 361,224 para la relación de aspecto de 4.5.

 

ANALISIS DE LA FLEXIBILIDAD LATERAL DEL DIAFRAGMA

Dado que el estudio evalúa la potencial flexibilidad del sistema de piso ante carga lateral, en los análisis de todos los modelos en estudio se aplicaron sobre las losas cargas laterales uniformemente distribuidas en cada nivel, en forma de presiones en ambos lados exteriores (perímetros) de la losa, las cuales modelan de una manera más realista las cargas laterales por sismo si el diafragma de piso se puede deformar en ese plano (figura 15). Se aplicaron en cada borde cargas laterales equivalentes a 5 t/m en los edificios de vivienda y de 7.5 t/m para los edificios de oficina. Dado que los análisis son elásticos lineales, la magnitud de la carga lateral empleada no es del todo relevante, pero cabe señalar que se seleccionó para que los desplazamientos laterales obtenidos en Ansys fueran razonables (ni muy chicos ni muy grandes), y así evitar imprecisiones por truncación numérica.

Paralelamente, se definieron como sistemas de piso de referencia a los sistemas de piso infinitamente rígidos (tanto para vivienda como para oficinas), tomando como base los modelos con losas perimetralmente apoyadas, modificando el módulo de elasticidad de la losa, de forma tal que se comportase como un diafragma infinitamente rígido, es decir, todos sus bordes no se deforman, por lo que el diafragma se mueve perfectamente como un cuerpo rígido. Para este propósito, se empleó entonces un módulo de elasticidad 100,000 veces mayor que el del concreto de las losas, es decir, E_DR=100,000E_c.

Distribución de desplazamientos laterales

En todos los modelos se definieron puntos de referencia en cada nivel para monitorear los desplazamientos laterales que se presentan en los ejes centroidales donde se ubican las columnas y en el centro de los diafragmas. Con la finalidad de facilitar la comparación del comportamiento de cada sistema de piso, en las figuras 16 y 17 se presentan, para todas las relaciones de aspecto en planta (A/B), los perfiles de los desplazamientos laterales (Δ) obtenidos en el último nivel de los distintos sistemas de piso en estudio normalizados con respecto a los desplazamientos en ese mismo nivel de los modelos de referencia donde el diafragma es infinitamente rígido (Δ_RÍGIDO). Se toman como referencia los desplazamientos obtenidos en ambos marcos perimetrales, así como el máximo desplazamiento lateral obtenido en el interior, que en algunas ocasiones correspondió a un marco interior y en otros casos al centro de un diafragma, como se reporta con detalle en Chinchilla (2012).

En la figura 16 se ilustran las amplificaciones de los desplazamientos laterales obtenidos para los sistemas de piso en edificios para vivienda en estudio. De estas gráficas se pueden hacer las siguientes observaciones:

(1) Las losas perimetralmente apoyadas (LPA) se mueven aparentemente como cuerpo rígido para todas las relaciones de aspecto en planta (A/B) en estudio; sin embargo, los desplazamientos laterales son en promedio 1.6 veces mayores a los que tendría un diafragma infinitamente rígido.

(2) El sistema de piso con base en vigueta y bovedilla (VyB) aparentemente también se desplaza como cuerpo rígido para todas las relaciones de aspecto en planta (A/B) en estudio y es, en promedio, aparentemente un poco más rígido que el sistema de piso con base en losa perimetralmente apoyada (LPA). Aquí cabe señalar que la bovedilla considerada es de gran calidad (muy rígida y resistente) y que se supuso en este estudio que el colado del firme sería de tal calidad que la acción compuesta sería total, lo que no se puede garantizar en todos los casos de interés práctico. También se observa que existen algunas pequeñas rotaciones (torsión), las cuales se deben tanto al comportamiento ortotrópico de este sistema de piso, como a que la distribución de viguetas y bovedillas en los tableros se alternó conforme a un tablero de ajedrez (figura 11), con la finalidad de balancear su rigidez y resistencia en las dos direcciones ortogonales principales.

(3) El sistema con base en losa plana reticular aligerada (LRA) con casetones de 40 cm x 40 cm es el más flexible de todos, ya que los desplazamientos laterales son en promedio 1.9 veces mayores a los que tendría un diafragma infinitamente rígido, aunque aparentemente también se desplaza razonablemente como cuerpo rígido para todas las relaciones de aspecto en planta en estudio (A/B).

En la figura 17 se ilustran las amplificaciones de los desplazamientos laterales obtenidos para los sistemas de piso en edificios para oficina en estudio y, para facilitar la visualización, se separaron los resultados obtenidos para losas reticular aligerada (LRA, figura 17b) de las de losas perimetralmente apoyadas (LPA, figura 17a) y losacero (LAC, figura 17a). De los resultados presentados en estas gráficas se pueden hacer las siguientes observaciones:

(1) Las losas perimetralmente apoyadas (LPA) se mueven aparentemente como cuerpo rígido para relaciones de aspecto en planta (A/B) entre 1.0 y 2.25; sin embargo, los desplazamientos laterales son en promedio 1.8 veces mayores a los que tendría un diafragma infinitamente rígido, lo que indica una cierta flexibilidad lateral. La flexibilidad lateral se observa más claramente a partir de relaciones de aspecto en planta A/B ≥ 3, donde ya se comienzan a observar mayores amplificaciones en el interior con respecto a los marcos del perímetro, siendo más notable a medida que la relación A/B aumenta.

(2) Para el sistema de piso con base en losacero (LAC) se amplifican en menor medida los desplazamientos laterales con respecto al sistema de piso de losa perimetralmente apoyada (LPA); sin embargo, para todas relaciones de aspecto en planta A/B, se observa una mayor amplificación en el interior del sistema de piso con respecto a los marcos del perímetro. Esta diferencia va en aumento a medida que la relación A/B también aumenta, lo cual no es un comportamiento típico de un diafragma rígido y si confirma que existe una incipiente flexibilidad lateral en este sistema de piso.

(3) El sistema con base en losa plana reticular aligerada (LRA) con casetones de 100 cm x 100 cm es, por mucho, el más flexible de todos, ya que los desplazamientos laterales son entre 5.5 y 6.0 veces mayores a los que tendría un diafragma infinitamente rígido (figura 17b). Es de llamar la atención que para relaciones de aspecto A/B entre 1.0 y 3.0, el sistema de piso aparentemente se desplaza también como cuerpo rígido; sin embargo, a partir de relaciones de aspecto en planta A/B ≥ 3.75 se observa ya la mayor amplificación de los desplazamientos laterales en el interior de la planta con respecto a los marcos del perímetro, lo cual es típico de un diafragma que no es rígido.

Tomando como referencia estos resultados únicamente, queda claro que todos los sistemas en estudio no constituyen propiamente diafragmas rígidos. No obstante, parece que para los edificios para vivienda en estudio, los sistemas de piso podrían considerarse razonablemente rígidos (quizás con la excepción de la losa reticular aligerada), mientras que para los edificios para oficinas, parece que todos los sistemas en estudio no son rígidos a partir de relaciones de aspecto en planta A/B≥3, y en el caso de la losa reticular aligerada, pues las amplificaciones de los desplazamientos con respecto a un sistema con diafragma rígido son tan grandes, que sugieren que aunque para algunas relaciones de aspecto en planta pudiese parecer que se mueve como cuerpo rígido, el sistema de piso en realidad proporciona una flexibilidad lateral nada despreciable a la estructura.

Para contestar a estas interrogantes se evaluaron otros parámetros, como fue el monitorear cómo los sistemas de piso distribuyen las fuerzas laterales entre los elementos verticales resistentes (en este caso, los marcos), como se discute en la siguiente sección.

Distribución de fuerzas cortantes basales en los marcos

Una característica de un diafragma rígido es que las fuerzas que absorben los elementos verticales resistentes son proporcionales a su rigidez lateral. Por lo tanto, en este estudio y ante la ausencia de excentricidades naturales de importancia, debido a que todos los marcos son iguales para un edificio en estudio dado, entonces todos los marcos deben de tomar el mismo cortante basal sin importar su ubicación en planta (perímetro o centro). También se sabe que en un diafragma totalmente flexible, si todos los marcos son iguales (como en este estudio), los marcos que se ubican en el centro de la planta toman una mayor proporción de las fuerzas laterales que los marcos del perímetro.

Por lo tanto, para cada sistema de piso en estudio se determinaron los cortantes basales que toman cada marco y éstos se normalizaron con respecto al cortante basal mínimo, que en todos los casos correspondió al de los marcos del perímetro.

En la figura 18 se presentan los resultados para los sistemas de piso en estudio para vivienda, donde se aprecia que los marcos centrales toman entre un 7% y un 11% más de cortante con respecto a los marcos del perímetro para las losas perimetralmente apoyadas (figura 18a) y para la vigueta y bovedilla tradicional (figura 18b) para las relaciones de aspecto en planta en estudio y, como era de esperarse, el cortante en el marco central aumenta a medida que aumenta la relación de aspecto. Sin embargo, para la losa reticular aligerada con casetones de 40 x 40 cm, los marcos centrales toman entre 11% y 20.5% más cortante que los marcos del perímetro (figura 18c), lo que confirma que, en efecto, son más flexibles que los otros dos sistemas en estudio.

En la figura 19 se presentan los resultados para los sistemas de piso en estudio para oficinas, donde se aprecia que los marcos centrales toman entre un 10% y un 32% más de cortante con respecto a los marcos del perímetro para las losas perimetralmente apoyadas (figura 19a), entre un 16% y un 44% más para la losacero (figura 19b), y entre un 21% y un 44% para la losa reticular aligerada con casetones de 100 x 100 cm (figura 19c). También se aprecia que la amplificación de los cortantes basales en los marcos centrales es más apreciable en la losa perimetralmente apoyada y en la losacero a partir de relaciones de aspecto en planta A/B≥3 (figuras 19a y 19b), mientras que en la losa plana aligerada en estudio es importante desde A/B=1 (figura 19c). Tomando como referencia este parámetro, se puede concluir que la losacero se comporta un poco más como un diafragma flexible que la losa reticular, aunque tomando como referencia el perfil de desplazamientos de los diafragmas (por ejemplo, figura 17), esto no pareciera ser.

Los resultados ya discutidos con la distribución de fuerzas cortantes basales en los marcos confirman que todos los sistemas en estudio no constituyen propiamente diafragmas totalmente rígidos, pero también confirman que tampoco son totalmente flexibles. Para los sistemas de piso para edificios para vivienda en estudio, éstos pudieran considerarse razonablemente rígidos, con la excepción de la losa reticular aligerada (semi-rígidos), mientras que para los edificios para oficinas, se confirma que todos los sistemas en estudio no son rígidos a partir de relaciones de aspecto en planta A/B≥3, y en el caso de la losa reticular aligerada con casetones de 100 x 100 cm, aún para relaciones de aspecto en planta menores.

Índices de flexibilidad

Para poder catalogar a los sistemas de piso como diafragmas rígidos, semi-rígidos, semi-flexibles o flexibles de una manera práctica, se requiere de índices que sean relativamente fáciles de aplicar. Por ello, a continuación se evalúan dos índices propuestos en la literatura, que tienen la característica de ser relativamente fáciles de aplicar y que se basan en los desplazamientos laterales obtenidos en los sistemas de piso.

El índice de flexibilidad más conocido es el propuesto en reglamentos y recomendaciones de diseño de los Estados Unidos, como por ejemplo el UBC-97 (1997), ASCE-7 (2010) y FEMA-368 (2001), donde se define a un diafragma como flexible, para fines de la distribución de fuerzas cortantes y momentos torsionantes de piso, cuando el desplazamiento lateral máximo del diafragma excede dos veces el desplazamiento lateral promedio de entrepiso, calculándose este último a partir de promediar los desplazamientos laterales obtenidos en los elementos verticales resistentes adyacentes (por ejemplo, marcos y/o muros), como se ilustra en la figura 20 y se indica en la ecuación 1, donde Δ₁ y Δ₂ son los desplazamientos de los marcos del perímetro y Δ_c es el desplazamiento máximo del diafragma. En caso contrario, el diafragma debe considerarse como rígido para fines prácticos.

Este índice fue propuesto, en los documentos de referencia, con base en los resultados analíticos y experimentales obtenidos en estructuras con sistemas de piso ligeros con base en madera contrachapada (triplay), los cuales, como se discutió en la introducción, son muy flexibles dado su poco espesor. Sin embargo, a-priori, no parece un índice adecuado para sistemas de piso como los estudiados, donde aunque las amplificaciones relativas en el perfil de los desplazamientos laterales del sistema de piso no son muy notables (figuras 16 y 17), si existen en cambio amplificaciones no del todo despreciables en las fuerzas cortantes que absorben los marcos centrales con respecto a los del perímetro (figura 19).

Los resultados obtenidos con este índice para todos los modelos en estudio y para cada nivel se reportan con detalle en Chinchilla (2012). Sin embargo, con fines de salvar espacio, el lector puede deducir, a partir de los resultados mostrados en la figura 16, que para los sistemas de piso para vivienda en estudio, este índice estuvo siempre muy cercano a 1.0 (máximo valor de R_ASCE-7=1.01), por lo que, de acuerdo con este índice, todos los sistemas de piso para vivienda constituyen diafragmas rígidos. A partir de la observación de la figura 17 se puede concluir que, de acuerdo con este índice, los sistemas de piso en estudio para edificios para oficinas también son diafragmas rígidos, pues de hecho, el valor máximo de este índice se obtuvo para losacero cuando A/B=4.5 (figura 17a) y fue R_ASCE-7=1.19. Sin embargo, la amplificación de las fuerzas cortantes basales en los marcos del centro con respecto a los del perímetro, particularmente para A/B≥3 (figura 19), sugieren que esta condición no es totalmente cierta. Por lo tanto, se puede concluir que aunque este índice es muy efectivo para identificar a un diafragma totalmente flexible, con él no se puede determinar si un diafragma es rígido, semi-rigido y semi-flexible y, por ello, no es de utilidad para clasificar a los sistemas de piso en estudio.

Un índice muy útil para evaluar la flexibilidad o rigidez del diafragma es el propuesto por Ju y Lin (1999). Para la obtención del índice de rigidez (R) se utilizan dos desplazamientos: a) el desplazamiento en el centro del claro del sistema de piso que se modeló considerando su potencial flexibilidad y, b) el desplazamiento en el centro del claro del sistema de piso considerando una rigidez infinita en su modelado. Por lo tanto, el índice de Ju y Lin está dado por:

donde Δ_flexible es el máximo desplazamiento del diafragma cuya flexibilidad se evalúa y Δ_rigido es el desplazamiento como diafragma rígido de esa misma estructura. Con base en los resultados de su extenso estudio paramétrico empleando elementos finitos, Ju y Lin (1999) demuestran que para valores de R < 0.2, la hipótesis en el análisis de diafragma rígido es bastante aproximada teniendo errores menores al 20% en la obtención de momentos flexionantes y fuerzas cortantes en los elementos más demandados y, para valores de R > 0.45, un análisis con base en la hipótesis de diafragma rígido conduce a errores de más del 40% en los momentos flexionantes y fuerzas cortantes de los elementos más demandados, por lo que debiera analizarse el sistema de piso considerando la potencial flexibilidad del sistema de piso en cuestión. Por lo tanto, para el intervalo 0.2≤ R ≤ 0.45, el comportamiento pudiera considerarse como semi-rígido o semi-flexible.

Con base en lo anterior, se calculó el índice de Ju y Lin para todos los diafragmas en todos los niveles y para todas las relaciones de aspecto en planta A/B de los edificios en estudio, tal y como se reporta con detalle en Chinchilla (2012). En las tablas 4 y 5 se reportan los valores máximos del índice R de Ju y Lin obtenidos en cada nivel para los sistemas de piso para vivienda y para oficinas en estudio. En general, se observa de las tablas 4 y 5 que, para todos los sistemas de piso en estudio, el índice R aumenta conforme se aumenta el nivel. Con esta observación parecería natural y conservador entonces evaluar la condición de diafragma con base en calcular el índice R con los desplazamientos obtenidos para los diafragmas del último nivel. Si se tomaran entonces los resultados de R del nivel 3 para evaluar la condición de diafragma, la conclusión sería, con base en lo propuesto por Ju y Lin, que para los edificios para vivienda (tabla 4), los sistemas de losa reticular aligerada con casetones de 40 x 40 cm deberían analizarse como flexibles, dado que R>0.45; sin embargo, de la figura 18c se aprecia que las amplificaciones de los cortantes basales de los marcos centrales con respecto al perímetro no superan el 21%, por lo que tal recomendación sería innecesariamente conservadora. En cambio, si se toman como más representativos los resultados del primer nivel, se obtiene que R oscila entre 0.368 y 0.389, por lo cual este sistema de piso debería considerarse semi-flexible, tal vez una valoración más adecuada.

De manera similar, si se usaran los valores de R del nivel 3 para definir la condición de diafragma de los sistemas de piso de losa perimetralmente apoyada y de vigueta y bovedilla, la conclusión sería que constituyen diafragmas semi-flexibles. Sin embargo, si usa uno los resultados del nivel 1, la conclusión es que se comportan más como diafragmas semi-rígidos y, con base en los resultados mostrados en las figuras 18a y 18b, esa es una descripción más próxima, pues incluso se podrían considerar como rígidos para fines prácticos.

Tomando ya como base los valores de R del nivel 1 para definir la condición de diafragma de los sistemas de piso de los edificios para oficinas (tabla 5), las conclusiones serían que para los sistemas de piso de losa perimetralmente apoyada y losacero se comportan más como diafragmas semi-flexibles, y con base en los resultados mostrados en las figuras 19a y 19b, esta descripción sería más próxima cuando A/B≥3. Para el caso de la losa reticular aligerada con casetones de 100 cm x 100 cm, los valores de R del nivel 1 (R > 0.45) indicarían que el sistema de piso se comporta como un diafragma flexible; sin embargo, los resultados de la figura 19c sugieren que más bien se comporta como un diafragma semi-flexible, salvo para A/B=4.5.

Cabe ahora señalar que en el estudio de Ju y Lin (1999), los sistemas de piso eran losas planas de concreto sólidas y que la valoración de su índice R con la diferencia de fuerzas de diseño (fuerzas cortantes y momentos) lo presentaron para sistemas cuyos elementos sismo-resistentes estaban compuestos por muros, donde la potencial condición de flexibilidad de diafragma se magnifica, dada la gran diferencia existente entre la rigidez lateral de los muros con respecto a la de los sistemas de piso y que, lamentablemente, Ju y Lin no presentaron estos mismos resultados para sus modelos con marcos, donde sólo comentaron que no encontraron grandes diferencias.

Por lo tanto, con base en los resultados obtenidos en este estudio se considera conveniente que, para potenciar al índice R propuesto por Ju y Lin para definir la condición de diafragma rígido o flexible, será necesario definir límites distintos, ya que se aprecia que estos dependen, entre otras variables, de las siguientes: (a) contraste de rigidez entre el sistema de piso y el sistema competente ante carga lateral (marcos, muros, estructuraciones mixtas), (b) las características del sistema de piso, (c) el claro libre que salvan los sistemas de piso y, (d) la relación de aspecto en planta.

Clasificación preliminar de los sistemas de piso en estudio

Los estudios reportados en Chinchilla (2012) son detallados y extensos, pero aún resultan insuficientes para proponer una clasificación robusta del comportamiento como diafragma de los sistemas de piso en estudio, pues se requieren realizar muchos más análisis de todo tipo para evaluar distintas variables. Sin embargo, si constituyen un primer paso que permiten proponer, de manera preliminar, cómo deben clasificarse los sistemas de piso en estudio utilizados en edificios estructurados con marcos a momento con base en: (a) la amplificación de las fuerzas cortantes de los marcos centrales con respecto a los marcos del perímetro (figuras 18 y 19) y, (b) la amplificación de los desplazamientos laterales de los sistemas de piso con respecto a sistemas que poseen diafragmas infinitamente rígidos (figuras 16 y 17).

De esta manera, para fines prácticos en las tablas 6 y 7 se presenta una propuesta de clasificación con base en la relación de aspecto en planta, donde también se consideran implícitamente otras variables como: (1) las características del sistema de piso y, (2) el claro libre que salvan los sistemas de piso. En dichas tablas, R indica un diafragma rígido, SR un diafragma semi-rígido, SF un diafragma semi-flexible y F a un diafragma flexible.

Conforme a lo propuesto en las tablas 6 y 7, se puede concluir que, a excepción de los sistemas de piso con base en losa reticular aligerada, para fines prácticos, todos los sistemas de piso en estudio pueden considerarse como diafragmas rígidos para relaciones de aspecto en planta A/B≤2.5, por lo que parece razonable el límite de 2.5 propuesto en los recomendaciones de diseño sísmico de México (NTCS-04 2004, MOC-2008 2009) para la relación de aspecto en planta para considerar a un edificio como regular.

Finalmente, con la información disponible en este estudio, es muy difícil proponer una clasificación alterna que defina con certidumbre los intervalos del índice R de Ju y Lin asociados a esta condición para cada sistema de piso. Sin embargo, para el caso de los edificios con base en marcos estudiados, parecería que la siguiente clasificación pudiera ser razonablemente práctica de manera preliminar: diafragma rígido R ≤ 0.25, diafragma semi-rígido 0.25< R ≤ 0.35, diafragma semi-flexible 0.35 < R ≤ 0.45 y diafragma flexible R > 0.45. Estos valores deberán pulirse con más estudios que valoren, además, el impacto de otras variables importantes para cada sistema de piso (por ejemplo, separación de vigas secundarias, espesores de firmes, dimensiones de casetones, rigidez de bovedillas, acción compuesta total o parcial, etc.).

 

COMENTARIOS FINALES Y CONCLUSIONES

En el presente estudio se evaluó, mediante análisis elásticos, el comportamiento de diafragma de los sistemas de piso más empleados en edificación urbana en México: losa perimetralmente apoyada, vigueta y bovedilla, losacero y losa reticular aligerada con bloques de espuma de poliestireno o casetones de fibra de vidrio, para edificios con base en marcos a momento, que constituye actualmente el sistema estructural más popular para edificios urbanos en México, y cuya flexibilidad lateral aparentemente reduce el impacto de la flexibilidad de los sistemas de piso con respecto a sistemas estructurales más rígidos lateralmente, como muros de cortante y estructuraciones mixtas (marcos con contravientos y/o muros). Es importante recalcar que todos los sistemas de piso fueron diseñados para satisfacer las condiciones de carga y de servicio conforme a la normatividad vigente y prácticas de diseño empleadas actualmente en despachos de diseño estructural de prestigio.

En esta investigación se consideraron dos factores identificados en estudios previos que favorecen la potencial flexibilidad del diafragma: a) la relación de aspecto de la planta del edificio y, b) la rigidez del sistema de piso, que es función de los espesores, módulos de elasticidad y distribución espacial de los materiales que los componen.

Para evaluar la potencial condición de flexibilidad de diafragma de los sistemas de piso, para cada sistema de piso y relación de aspecto de la planta en estudio, se realizaron análisis elásticos ante carga lateral uniformemente distribuida en el sistema de piso en modelos de elementos finitos empleando el programa Ansys. Se emplearon tanto formulaciones isotrópicas para modelar a los elementos que componen a los marcos, como formulaciones ortotrópicas para modelar a los sistemas de piso cuyas rigideces en sus direcciones ortogonales principales son distintas (por ejemplo, vigueta y bovedilla y losacero). Paralelamente, se definieron a sistemas de piso infinitamente rígidos de referencia, tomando como base los modelos con losas perimetralmente apoyadas y modificando el módulo de elasticidad de la losa, de forma tal que se comportase como un diafragma infinitamente rígido.

La condición de diafragma se evaluó por medio de los siguientes parámetros: (a) los perfiles de los desplazamientos laterales (Δ) obtenidos en el último nivel de los distintos sistemas de piso en estudio, normalizados con respecto a los desplazamientos en ese mismo nivel de los modelos donde el diafragma es infinitamente rígido (Δ_RÍGIDO) y, (b) el factor de amplificación del cortante basal de los marcos centrales con respecto a los marcos del perímetro. Se evaluaron también dos índices de flexibilidad (rigidez) propuestos en la literatura: a) el índice propuesto en normas de los Estados Unidos como el UBC-97, ASCE-7 y FEMA-368 y, b) el índice propuesto por Ju y Lin en 1999.

Se observó, a partir de los perfiles de desplazamientos de los sistemas de piso, que aunque los sistemas de piso en estudio para edificios para vivienda aparentemente se mueven como cuerpo rígido para todas las relaciones de aspecto en planta (A/B) consideradas, los desplazamientos laterales son en promedio más de 1.6 veces mayores a los que tendría un diafragma infinitamente rígido. Para los sistemas de piso en estudio para edificios para oficinas, se aprecia algo similar para relaciones de aspecto en planta A/B entre 1.0 y 2.25. Sin embargo, la flexibilidad lateral se observa más claramente a partir de relaciones de aspecto en planta A/B ≥ 3, dado que se observa una mayor amplificación en el interior del sistema de piso con respecto al perímetro, siendo más notable a medida que la relación A/B aumenta. Por lo tanto, se puede concluir que todos los sistemas de piso en estudio no constituyen diafragmas rígidos propiamente.

Los resultados obtenidos a partir de comparar el factor de amplificación del cortante basal de los marcos centrales con respecto a los perimetrales, confirmaron que todos los sistemas en estudio no constituyen diafragmas totalmente rígidos. Para los sistemas de piso para edificios para vivienda en estudio, éstos pudieran considerarse razonablemente rígidos, con la excepción de la losa reticular aligerada (semi-rígido), mientras que para los edificios para oficinas, se confirma que todos los sistemas en estudio no son rígidos a partir de relaciones de aspecto en planta A/B≥3 (semi-rígidos o semi-flexibles), y en el caso de la losa reticular aligerada con casetones de 100 x 100 cm, aún para relaciones de aspecto en planta menores.

De acuerdo con los resultados obtenidos en este estudio paramétrico, se puede concluir que a excepción de los sistemas de piso con base en losa reticular aligerada, para fines prácticos, todos los sistemas de piso en estudio pueden considerarse como diafragmas rígidos para relaciones de aspecto en planta A/B≤2.5, por lo que parece razonable el límite A/B=2.5 propuesto en los recomendaciones de diseño sísmico de México (NTCS-04 2004, MOC-2008 2009) para considerar a un edificio como regular.

A partir de los resultados obtenidos en este estudio, se puede concluir que el índice de flexibilidad propuesto en reglamentos y recomendaciones de diseño de los Estados Unidos como el UBC-97, ASCE-7, FEMA-368 y similares, el cual fue desarrollado para identificar a diafragmas totalmente flexibles, a partir de investigaciones realizadas en sistemas de piso ligeros de madera contrachapada (triplay), aunque es muy efectivo para identificar esa condición, no permite determinar si un diafragma es rígido, semi-rigido o semi-flexible y, por ello, no es útil para evaluar a los sistemas de piso de mayor interés en la práctica mexicana. En este sentido, es mucho más útil el índice R propuesto por Ju y Lin, el cual tiene un enorme potencial de aplicación práctica e incluso reglamentaria. Sin embargo, aun es complicado hacer una propuesta que defina con certidumbre los intervalos del índice R de Ju y Lin para clasificar a los sistemas de piso como rígidos, semi-rígidos, semi-flexibles o flexibles. Para ello, será necesario conducir estudios paramétricos adicionales, que permitan evaluar las siguientes variables: (a) contraste de rigidez entre el sistema de piso y el sistema competente ante carga lateral (marcos, muros, estructuraciones mixtas), (b) las características del sistema de piso, (c) distintos claros libres que salven los sistemas de piso y, (d) las relaciones de aspecto en planta (A/B).

A partir de los resultados de este extenso estudio paramétrico se puede concluir que un sistema de piso bien diseñado, cumpliendo los reglamentos y las recomendaciones de diseño de los fabricantes, más la experiencia de prestigiados ingenieros de la práctica, nos puede liderar a diseñar sistemas de piso que se comportan razonablemente como diafragmas rígidos, sobre todo para edificios para vivienda o para otro uso, donde los claros de los marcos no sean muy grandes (6m o menos, con base en los resultados de este estudio). Sin embargo, esta observación no se puede generalizar, pues otras prácticas de diseño pudieran favorecer la presencia de diafragmas semi-rígidos, semi-flexibles o claramente flexibles.

Por ejemplo, en este estudio se obtuvieron resultados que sugieren que el sistema de piso con base en vigueta y bovedilla pudiera comportarse como un diafragma rígido. Sin embargo, aquí cabe señalar que la bovedilla considerada en este estudio es de gran calidad y muy rígida, y que además se supuso una acción compuesta total con el firme de concreto, lo que requiere de detallado especial. Si no existe acción compuesta total, la rigidez del conjunto disminuye por esta sola razón. Por otra parte, debería resulta claro que si se hubiese estudiado una bovedilla de espuma de poliestireno (que se está poniendo de moda, figura 1a), material cuya rigidez es despreciable, entonces los resultados no hubiesen sido tan favorables, pues la rigidez lateral del sistema de piso se reduciría notablemente. Además, la vigueta y bovedilla se alternó a lo largo y ancho del sistema de piso como tablero de ajedrez, lo que balanceó la rigidez y la resistencia del diafragma en las dos direcciones ortogonales. Si se hubiese considerado que las viguetas y bovedillas se disponen en una sola dirección, la rigideces en direcciones ortogonales serían muy distintas, y el sistema de piso sería notablemente menos rígido y resistente en la dirección perpendicular a las viguetas. Esta es una mala práctica que lamentablemente aún se construye en edificios de este país.

Con respecto a la losacero, en este estudio se evaluó una buena práctica, que consiste en apoyar a la lámina de acero cada 2.0 metros en las vigas secundarias con base en perfiles I de acero estructural, y se consideró acción compuesta total entre la lámina de acero y el firme de concreto, para lo cual deben diseñarse los conectores de cortante, además de disponerse la losacero a lo largo y ancho del sistema de piso como tablero de ajedrez. Si la acción compuesta total no se puede garantizar, la rigidez lateral del sistema de piso disminuye. Si los perfiles I se disponen a distancias mayores a las aquí consideradas, la rigidez del sistema de piso también disminuye. Si la lámina acanalada de acero se dispone en una sola dirección, la rigidez y la resistencia de la losacero en la dirección perpendicular a las viguetas será menor y sí, esta es otra mala práctica muy arraigada, por lo que existen varios edificios en este país construidos de esta manera.

Con respecto a la losa plana reticular aligerada con casetones (daría prácticamente lo mismo con bloques de espuma de poliestireno, dada la rigidez despreciable de este material), los resultados de este estudio confirman que este sistema no puede considerarse rígido y demuestran que su rigidez disminuye notablemente a medida que el área del bloque hueco aumenta. Esta reducción de rigidez se puede demostrar observando la gran diferencia que se obtuvo en las amplificaciones de los desplazamientos laterales con respecto a un diafragma rígido entre los edificios para vivienda (1.9 en promedio), donde se consideraron huecos de 40 x 40 cm, y los edificios para oficina (entre 5.5 y 6 veces), donde se consideraron huecos de 100 x 100 cm. Es cierto que el incremento en la longitud del claro a salvar en los marcos favorece una amplificación; sin embargo, comparando los resultados que se obtuvieron para la losa perimetralmente apoyada, el factor de amplificación creció de 1.6 veces en promedio para los edificios para vivienda, a 1.8 veces en promedio para los edificios para oficinas (12.5% de diferencia). Por lo tanto, resulta claro que la rigidez lateral de la losa reticular aligerada se reduce más significativamente a medida que aumenta el área del hueco, a pesar que las nervaduras sean más robustas cuando los huecos son más grandes. Esta no es una observación menor; el primer autor conoce de construcciones recientes donde se utilizaron bloques de espuma de poliestireno rectangulares de aproximadamente 60 cm x 100 cm en edificios para vivienda de claros similares a los estudiados, para los cuales no se pueden extrapolar los resultados obtenidos en este estudio para huecos de 40x40cm; obviamente serán más flexibles.

También cabe destacar que en el presente estudio se consideraron que los edificios son con base en marcos a momento, que es el sistema mayoritariamente empleado hoy en día en la ciudad de México para edificios de oficinas y de vivienda. Se sabe que la condición de flexibilidad de diafragma la atenúan los edificios con base en marcos a momento, por su flexibilidad lateral, y que la magnifican los edificios estructurados con sistemas sismo-resistentes lateralmente más rígidos, por ejemplo, con base en muros o con estructuraciones mixtas (marcos con contravientos y/o muros). En México existen también una cantidad no despreciable de edificios con estos sistemas estructurales y donde se emplean los sistemas de piso estudiados. Por lo tanto, se deberá tomar en cuenta que, para esas estructuraciones, la condición de diafragma flexible se potencia, y que no sería conservador tomar como equivalente la clasificación propuesta en este estudio, la que sólo serviría como una referencia o límite inferior no conservador.

El presente estudio constituye un pequeño avance sobre el entendimiento de cuál es el comportamiento como diafragma de los sistemas de piso más utilizados actualmente en edificación urbana en México, por lo que se requieren de muchos estudios adicionales para poder dar guías o recomendaciones de índole práctica para el análisis y diseño de estructuras que no constituyan diafragmas rígidos o totalmente flexibles, sin la necesidad de elaborar modelos detallados en elementos finitos ¿Cómo se analiza y diseña, de manera simple, un edificio cuyo sistema de piso se comporta como un diafragma semi-rígido o semi-flexible? Esta es ciertamente una tarea pendiente que se deberá abordar en investigaciones futuras, en aras de mejorar la práctica profesional, con lo cual se ayudará a reducir la vulnerabilidad de nuestro nuevo inventario de estructuras, pues es una realidad que estas estructuras se seguirán construyendo por múltiples razones social y económicamente justificadas.

 

AGRADECIMIENTOS

Los autores agradecen a los ingenieros Francisco García Jarque, Francisco García Álvarez y Santiago García Álvarez, de García Jarque Ingenieros, por haber compartido con nosotros sus herramientas de diseño y sus experiencias sobre su práctica profesional de diseño de varios de los sistemas de pisos en estudio. Karen Lineth Chinchilla Portillo agradece la beca otorgada por Conacyt, que le permitió involucrarse en este proyecto de investigación en el desarrollo de su tesis de maestría.

 

REFERENCIAS

Al Harash, M. T., N. Panahshahi y K. Z. Truman (2008), "Inelastic seismic response of reinforced concrete buildings with floor diaphragm openings", Memorias, 14WCEE, Beijing, China, Artículo 05-01-0286, CDROM.         [ Links ]

Ansys (2009), Ansys 12.0.1, Ansys Inc., Estados Unidos.         [ Links ]

ASCE-7 (2010), "Minimum design loads for buildings and other structures", ASCE Standard ASCE/SEI 7-10, American Society of Civil Engineers, ISBN 0-7844-0809-2.         [ Links ]

Bal, I. E. y Z. Ozdemir (2006), "The adverse effects of perimeter frame discontinuity on earthquake response of RC buildings", Memorias, Seventh International Congress on Advances in Civil Engineering, Yildiz Technical University, Estambul, Turquía, octubre.         [ Links ]

Barron, J. M. y M. B. D. Hueste (2004), "Diaphragm effects in rectangular reinforced concrete buildings", ACI Structural Journal, Vol. 101, No. 5, pp. 615-624.         [ Links ]

Basu, D. y S. K. Jain (2004), "Seismic analysis of asymmetric buildings with flexible floor diaphragms", ASCE Journal of Structural Engineering, Vol. 130, No. 8, pp.1169-1176, agosto.         [ Links ]

Brignola, A., S. Podestà y S. Pampanin (2008), "In-plane stiffness of wooden floor", Memorias, 2008NZSEE Conference, Paper No. 49, CDROM, pp 1-19.         [ Links ]

Celebi, M., G. Bongiovanni, E. Safak y A. G. Brady (1989), "Seismic response of a large-span roof diaphragm", Earthquake Spectra, Vol. 5, No. 2, pp. 337-350.         [ Links ]

Chen, S.-J. (1986), "Reinforced concrete floor slabs under in-plane monotonic and cyclic loading", Ph.D. Thesis, Fritz Engineering Laboratory, Lehigh University, diciembre.         [ Links ]

Chen, S.-J., T. Huang y L.-W.- Lu (1988), "Diaphragm behavior of reinforced concrete slabs", Memorias, 9WCEE, Tokio-Kyoto, Japón, Vol. 4, pp. 565-570.         [ Links ]

Chinchilla, K. L. (2012), "Evaluación de la flexibilidad de diafragma en sistemas de piso utilizados en edificios urbanos", Tesis de Maestría, Posgrado en Ingeniería Estructural, División de Ciencias Básicas e Ingeniería, Universidad Autónoma Metropolitana Azcapotzalco, octubre.         [ Links ]

Cincúnegui, C. (2011), "Vigas compuestas y vibraciones, versión 3.4", México, D.F.         [ Links ]

Cohen, G. L., R. E. Klingner, J. R. Hayes y S. C. Sweeney (2004), "Seismic evaluation of low-rise reinforced masonry buildings with flexible roof diaphragms: I. Seismic and quasi-static testing", Earthquake Spectra, Vol. 20, No. 3, pp. 779-801.         [ Links ]

CSI-2005 (2005), "CSI analysis reference manual for SAP2000, ETABS, and SAFE", Computers and Structures, Inc., Berkeley, California, Estados Unidos, octubre.         [ Links ]

Damian, A., L. A. Kovacs, C. T. Bia, O. Gosa, H. Maniu, C. S. Dico y A. Tokes (2000), "Diaphragm behaviour of the floor with prestressed beam and filler blocks", Memorias, 12WCEE, Auckland, Nueva Zelanda, Artículo 0696, CDROM, febrero.         [ Links ]

De-La-Colina, J. (1999), "In-plane floor flexibility effects on torsionally unbalanced systems", Earthquake Engineering & Structural Dynamics, Vol. 28, No. 12, pp. 1705-1715, diciembre.         [ Links ]

Doudoumis, I. N. y A. M. Athanatopoulou (2001), "Code provisions and analytical modelling for the in-plane flexibility of floor diaphragms in building structures", Journal of Earthquake Engineering, Vol. 5, No. 4, pp. 565-594, octubre.         [ Links ]

FEMA-368 (2001), "NEHRP recommended provisions for seismic regulations for new buildings and other structures. Part 1: Provisions", FEMA Publication 368, Federal Emergency Management Agency, Washington, DC.         [ Links ]

Fleischman, R. B. y K. T. Farrow (2001), "Dynamic behavior of perimeter lateral-system structures with flexible diaphragms", Earthquake Engineering & Structural Dynamics, Vol. 30, No. 5, pp. 745-763, mayo.         [ Links ]

Fleischman, R. B., K. T. Farrow y K. Eastman (2002), "Seismic performance of perimeter lateral-system structures with highly flexible diaphragms", Earthquake Spectra, Vol. 18, No. 2, pp. 251-286, mayo.         [ Links ]

García Jarque (2011). Comunicación personal con los ingenieros Francisco García Jarque, Francisco García Álvarez y Santiago García Álvarez.         [ Links ]

IMSA (2011), "IMSA, Losacero sección 4 y sección 36/15, para un entrepiso más ligero", http://www.perfilesviaductotlalpan.com/ManualLosacero.pdf.         [ Links ]

Ju, S. H. y M. C. Lin (1999), "Comparison of building analyses assuming rigid or flexible floors", ASCE Journal of Structural Engineering, Vol. 125, No. 1, pp. 25-31.         [ Links ]

Karadogan, H. F., T. Huang, L.-W. Lu y M. Nakashima (1980), "Behavior of flat plate floor systems under in-plane seismic loading", Memorias, 7WCEE, Estambul, Turquía, Vol. 5, pp. 9-16.         [ Links ]

Kim, S.-C. y D. W. White (2004), "Linear static analysis of low-rise buildings with flexible diaphragms using the structural separation method", Engineering Structures, Vol. 26, No. 1, pp. 83-93, enero.         [ Links ]

Kolston, D. y B.W. Buchanan (1980), "Diaphragms in seismic resistant buildings", Bulletin of the New Zealand National Society for Earthquake Engineering, Vol. 13, No. 2, pp. 162-170, junio.         [ Links ]

Kunnath, S. K., N. Panahshahi y A. M. Reinhorn (1991), "Seismic response of RC buildings with inelastic floor diaphragms", ASCE Journal of Structural Engineering, Vol. 117, No. 4, pp. 1218-1237.         [ Links ]

Langroudi, J. R., M. M. Ranjbar, S. J. Hashemi y A. S. Moghadam (2011), "Evaluation of roof diaphragm effect on seismic behavior of masonry buildings", Memorias, 8th International Conference on Structural Dynamics EURODYN2011, Leuven, Bélgica, pp. 453-458, julio.         [ Links ]

Lee, H. J., D. Kuchma y M. A. Aschheim (2007) "Strength-based design of flexible diaphragms in low-rise structures subjected to earthquake loading", Engineering Structures, Vol. 29, No. 7, pp. 1277–1295, julio.         [ Links ]

León, G. A. (2007), "Comportamiento sísmico de edificios con losa de vigueta y bovedilla, para distintas ubicaciones de las viguetas en planta", Memorias, XVI Congreso Nacional de Ingeniería Sísmica, Ixtapa-Zihuatanejo, Artículo V-07, CDROM, pp. 1-25, noviembre.         [ Links ]

López, O., A. H. Cazamayor, E. Ortiz y H. Silva (2001), "Estudio experimental sobre el comportamiento de estructuras con sistema de piso de vigueta y bovedilla sujetas a cargas laterales", Memorias, XIII Congreso Nacional de Ingeniería Sísmica, Guadalajara, CDROM, pp. 1-15, noviembre.         [ Links ]

López, O. A. y E. Raven (1999), "An overall evaluation of irregular-floor-plan shaped buildings located in seismic areas", Earthquake Spectra, Vol. 15, No. 1, pp. 105-120, febrero.         [ Links ]

Mastrogiuseppe, S., C. A. Rogers, R. Tremblay y C. D. Nedisan (2008), "Influence of nonstructural components on roof diaphragm stiffness and fundamental periods of single-storey steel buildings", Journal of Constructional Steel Research, Vol. 64, No. 2, pp. 214-227.         [ Links ]

MOC-2008 (2009), "Manual de diseño de obras civiles. Diseño por sismo", Comisión Federal de Electricidad, diciembre.         [ Links ]

Moeini, M. y B. Rafezy (2011), "Investigation into the floor diaphragms flexibility in reinforced concrete structures and code provision", Global Journal of Researches in Engineering, Vol. 11, No. 1, pp. 25-35, febrero.         [ Links ]

Naeim, F. y R. R. Boppana (2001), "Chapter 8: Seismic design of floor diaphragms", The Seismic Design Handbook, segunda edición, Kluwer Academic Publishers, pp. 373-407, ISBN 978-0-7923-7301-8.         [ Links ]

Nakashima, M., T. Huang y L.-W. Lu (1984), "Effect of diaphragm flexibility on seismic response of building structures", Memorias, 8WCEE, San Francisco, California, Vol. 4, pp. 735-742.         [ Links ]

NTCC-04 (2004), "Normas Técnicas Complementarias para diseño y Construcción de Estructuras de Concreto", Gaceta Oficial del Distrito Federal, octubre.         [ Links ]

NTCS-04 (2004) "Normas Técnicas Complementarias para Diseño por Sismo", Gaceta Oficial del Distrito Federal, Tomo II, No. 103-BIS, octubre, pp. 55-77.         [ Links ]

Öztürk, T. (2011), "A study of the effects of slab gaps in buildings on seismic response according to three different codes", Scientific Research and Essays Vol. 6, No. 19, pp. 3930-3941.         [ Links ]

Panahshahi N., A. M. Reinhorn, S. K. Kunnath, L.-W. Lu, T. Huang y K. Yu (1991), "Seismic response of a 1:6 reinforced concrete scale-model structure with flexible floor diaphragms", ACI Structural Journal; Vol. 88, No. 3, pp. 615-624.         [ Links ]

Paulte, P., J. Proulx, C. E. Ventura, R. Tremblay, C. A. Rogers, C.-P. Lamarche y M. Turek (2004), "Experimental investigation and dynamic simulations of low-rise steel buildings for efficient seismic design", Memorias, 13^th World Conference on Earthquake Engineering, Vancouver, Canadá, Artículo No. 2919, agosto.         [ Links ]

Pinho, R., C. Bhatt, S. Antoniou y R. Bento (2008), "Modelling of the horizontal slab of a 3D irregular building for nonlinear static assessment", Memorias, 14WCEE, Beijing, China, Artículo 05-010159, CDROM.         [ Links ]

PREMEX (2011). Manual PREMEX, http://www.premex.com.mx.         [ Links ]

RCDF-04 (2004), "Reglamento de Construcciones del Departamento del Distrito Federal", Gaceta Oficial del Departamento del Distrito Federal, octubre.         [ Links ]

Rodríguez, M., S. Santiago y R. Meli (1995), "Seismic load test on two-story waffle-flat-plate structure", ASCE Journal of Structural Engineering, Vol. 121, No. 9, pp. 1287-1293.         [ Links ]

Sadashiva, V. K., G. A. MacRae, B. L. Deam y M. S. Spooner (2012), "Quantifying the seismic response of structures with flexible diaphragms", Earthquake Engineering and Structural Dynamics, Vol. 41, No. 10, pp. 1365-1389, doi: 10.1002/eqe.1187.         [ Links ]

Saffarini, H. S. y M. M. Qudaimat (1992), "In-plane floor deformations in RC structures", ASCE Journal of Structural Engineering, Vol. 118, No. 11, pp. 3089-3102.         [ Links ]

Sarkissian, L., K. K. Jahromi y S.M. Zahrai (2006), "Impact of joists direction on the diaphragm behavior of composite floor systems", JSEE, Vol. 8, No. 1, pp. 29-38.         [ Links ]

Tena-Colunga, A. (1992), "Seismic evaluation of unreinforced masonry structures with flexible diaphragms", Earthquake Spectra, Vol. 8, No. 2, pp. 305-318, mayo.         [ Links ]

Tena-Colunga, A. y D. P. Abrams (1992), "Response of an unreinforced masonry building during the Loma Prieta Earthquake", Structural Research Series No. 576, Department of Civil Engineering, University of Illinois at Urbana-Champaign, diciembre.         [ Links ]

Tena-Colunga, A. y D. P. Abrams (1995), "Simplified 3-D dynamic analysis of structures with flexible diaphragms", Earthquake Engineering & Structural Dynamics, Vol. 24, No. 2, pp. 221-232, febrero.         [ Links ]

Tena-Colunga, A. y D. P. Abrams (1996), "Seismic behavior of structures with flexible diaphragms", ASCE Journal of Structural Engineering, Vol. 122, No. 4, pp. 439-445, abril.         [ Links ]

Tena, A. y J. A. Cortés (2009), "Valoración de la rigidez del diafragma para el empleo del método simplificado de diseño sísmico de los reglamentos de México en estructuras de manipostería", Boletín Técnico IMME, Vol. 47, No. 3, pp. 25-39.         [ Links ]

Tena, A. (2010), "Irregularidad estructural y su efecto en la respuesta sísmica de edificios", Memorias V Congreso Iberoamericano de Ingeniería Civil en honor del Dr. José Grases, Mérida, Venezuela, CD-ROM pp 1-57, noviembre.         [ Links ]

Tremblay, R. y S. F. Stiemer (1996), "Seismic behavior of single-storey steel structures with a flexible roof diaphragm", Canadian Journal of Civil Engineering, Vol. 23, No. 1, pp. 49-62.         [ Links ]

UBC-97 (1997), "Uniform Building Code. 1997 edition", International conference of building officials, Vol. 2.         [ Links ]

 

Nota

* Se aceptarán comentarios y/o discusiones hasta cinco meses después de su publicación.