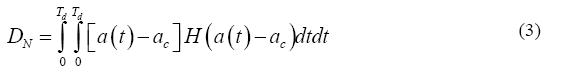Artículos

 

Una aproximación para la obtención de mapas de desplazamiento traslacional de laderas a nivel regional inducido por sismos*

 

Miguel A. Jaimes¹, Mauro Niño¹ , Eduardo Reinoso¹

 

¹ Instituto de Ingeniería, UNAM, Ciudad Universitaria, 04510 México, D.F. mjaimest@iingen.unam.mx, mninol@iingen.unam.mx, ereinosoa@iingen.unam.mx.

 

Artículo recibido el 15 de febrero de 2011.
Aprobado para su publicación el 27 de agosto de 2013.

 

Resumen

Se propone una expresión para estimar el desplazamiento de Newmark en términos de la relación entre la aceleración crítica, a_c (umbral de aceleración del suelo para iniciar un movimiento del talud) y la aceleración máxima del suelo, a_max, para obtener el deslizamiento traslacional de laderas por sismo que de manera aproximada estimen esta amenaza a escala regional. Con los resultados que se obtienen de la ecuación de desplazamiento propuesta es posible definir un mapa de peligro sísmico por deslizamiento traslacional a nivel regional inducido por sismo. Para llevar a cabo lo anterior, se asumen valores promedio de propiedades mecánicas del suelo como la cohesión, peso volumétrico y ángulo de fricción a partir de mapas geológicos y litológicos a escala 1:1'000,000, así como la pendiente de deslizamiento potencial a partir de modelos de elevación digital del terreno. Se presenta un mapa de peligro de deslizamiento de la República Mexicana asociado a la aceleración máxima del suelo que se presenta con un periodo de retorno de 150 años, y un ejemplo de un mapa empleando como detonador el sismo de Tecomán en Colima de magnitud M=7.6 ocurrido el 21 de enero de 2003; este ejemplo se compara con el obtenido a través del método Mora-Vahrson que es ampliamente utilizado para elaborar este tipo de mapas de deslizamientos.

Palabras Clave: mapas de deslizamiento traslacional, desplazamiento de Newmark, intensidad sísmica, evaluación del peligro por deslizamiento.

 

Abstract

We propose to obtain translational landslides due to earthquake in Mexico estimating Newmark displacements in terms of the relationship between the critical acceleration, a_c (the peak ground acceleration threshold to start the landslide) and the peak ground acceleration, a_max. With the obtained results from a proposed displacement equation it is possible to define a translational landslide map at regional level induced by earthquakes. Soil parameters such as cohesion, volumetric weight and angle of friction are inferred from geological maps, scale 1:1'000,000, and a digital elevation map is employed to obtain the slope of the potential landslide. We present a landslide hazard map for Mexico associated to a peak strong ground motion acceleration with a return period of 150 years at regional level, and an example map of displacements triggered by the Tecoman earthquake with M=7.6 occurred in January 21st, 2003; this case is compared with results from the Mora-Vahrson method which is widely used to obtain landslide hazard maps.

Key Words: translational landslide maps, Newmark displacement, seismic intensity, landslide hazard assessment.

 

INTRODUCCIÓN

México es un país cuyo territorio está conformado en dos terceras partes por sistemas montañosos donde se conjugan factores geológicos, geomorfológicos, estructurales y climáticos que definen zonas geológicamente inestables. Existen sobre ellos desarrollos urbanos y rurales así como infraestructura civil. Esto coloca a un gran número de habitantes y bienes expuestos en una situación de riesgo potencial ante la generación de deslizamientos y derrumbes de roca, flujos de lodos y detritos, así como otros procesos destructivos asociados a zonas montañosas.

Los distintos tipos de procesos de remoción en masa presentes en el país y que causan daño a bienes expuestos y a la población están íntimamente ligados a las condiciones geológicas y estructurales del relieve, a la influencia del clima y, en cierto grado, a la influencia antrópica, particularmente la deforestación (Alcántara-Ayala et al., 2006) y el drenaje. Por lo anterior, resulta fundamental el conocimiento y el análisis de las distintas formaciones geológicas que conforman el territorio nacional con el fin de establecer esquemas generales que relacionen al tipo de material con los problemas geotécnicos y de estabilidad de laderas. Esto es útil para relacionar los distintos procesos de remoción de masas (PRM) con cada formación geológica, establecer esquemas de mitigación y remediación, orientar acciones de gestión del riesgo a nivel regional y ser la base para gestiones a diferentes escalas.

Existen numerosos casos de PRM que han afectado a diversas regiones de México. Algunos estados del país son muy susceptibles a la ocurrencia de deslizamientos de gran magnitud y potencial destructivo porque presentan un relieve escarpado, litologías desfavorables y climas húmedos, como la costa sur de la República Mexicana (desde el estado de Chiapas hasta Guerrero), la costa del estado de Jalisco, los estados de Veracruz, Tabasco, Puebla, Hidalgo, Estado de México, Distrito Federal, Guanajuato, Baja California Norte y, en menor medida, algunas porciones de los estados de Sinaloa, San Luís Potosí, Durango, Zacatecas y Nuevo León. En general, aunque los desastres por deslizamientos en México se deben principalmente a fenómenos meteorológicos derivados de eventos de lluvias tales como huracanes, tormentas tropicales con su posible interacción con frentes fríos, los deslizamientos por sismos o los efectos combinados de sismos y lluvias representan un porcentaje importante en la ocurrencia de deslizamientos de laderas (Alcántara-Ayala, 2008).

Se ha observado que los sismos de moderada y gran magnitud pueden inducir deslizamientos de laderas que podrían ocasionar pérdidas por sismo en caminos y carreteras. Incluso, se ha documentado que un enorme deslizamiento puede ser disparado por un efecto combinado de cambio de presión de poro en el suelo debido a las lluvias y un muy pequeño sismo (Sassa et al. 2010). Una manera para estimar el posible deslizamiento traslacional de taludes ante la ocurrencia de un sismo es el uso del parámetro de desplazamiento de Newmark, D_N (Newmark, 1965) que es una medida del desplazamiento permanente de una porción de un talud causado por un movimiento sísmico a lo largo de su superficie. Este desplazamiento se modela como un bloque de fricción rígido que se desliza en un plano inclinado cuando está sujeto a un movimiento sísmico en su base. A pesar que en su definición se emplean parámetros cuantitativos, D_N no predice el desplazamiento real del deslizamiento en campo, pero es una herramienta útil para definir el comportamiento del talud. Wilson y Keefer (1985) proponen valores críticos de D_N correspondientes al umbral en el cual una ladera se puede deslizar, y sugieren valores de 10 y 2 cm para deslizamientos progresivos (flujo de bloques, flujo de tierra lento) y para deslizamientos súbitos (caídas, deslizamientos y avalanchas de roca), respectivamente. Por su parte, Wieczorek et al. (1985) han propuesto un esquema diferente de esta técnica para realizar una microzonificación de deslizamiento de laderas.

Existen otros métodos que definen, en términos de factores de susceptibilidad, la ocurrencia de un deslizamiento de laderas, como es el caso del método Mora-Vahrson (Mora y Vahrson, 1994), ampliamente utilizado en Latinoamérica por la sencillez en su aplicación a niveles regionales (Mora y Vahrson, 1993). Este método está basado en reglas empíricas cuyos resultados dependen de indicadores denominados morfodinámicos como la topografía del lugar, las condiciones litológicas, la humedad del suelo y la intensidad sísmica. Los indicadores anteriormente descritos se combinan considerando un peso ponderado que define el valor relativo de la amenaza por deslizamientos en términos cualitativos. Este método no tiene bases robustas que representen este fenómeno físico, y no proporciona información sobre la ocurrencia de dicho fenómeno. Por ello, se han continuado desarrollando metodologías basadas en la propuesta originalmente por Newmark (Jibson et al. 1998; Mankelow y Murphy, 1998; Jibson et al. 2000; Miles y Keefer, 2000, 2001; Rathje y Saygili, 2006). El esquema se ha validado para calcular deslizamientos importantes como los producidos en el sismo de Irpinia de 1980 (Del Gaudio y Wasowski, 2004) y Northridge de 1994 (Jibson et al. 2000; Jibson, 2007), y para la predicción de futuros escenarios (Del Gaudio y Wasowski, 2004). Estos estudios involucran el uso de sistemas de información geográfica (SIG) en el que se realizan estimaciones puntuales del desplazamiento para el sitio de interés. Para llevar a cabo un análisis de Newmark riguroso, sería necesario seleccionar una familia de movimientos sísmicos registrados o simulados para cada sitio, lo que resultaría impráctico. En la literatura existen diferentes modelos de regresiones empíricas para estimar el desplazamiento de Newmark como función de la aceleración crítica (Ambraseys y Menu, 1988; Jibson, 2007), la relación entre la aceleración crítica y la magnitud del sismo (Jibson, 2007) y la intensidad de Arias y la aceleración crítica (Jibson, 1993; Jibson et al. 1998, 2000; Jibson, 2007), y la aceleración máxima del suelo y la aceleración crítica (Jibson, 2007).

En este trabajo se plantea una expresión para estimar el valor de D_N en términos de la relación entre una aceleración crítica, a_c, y la aceleración máxima del suelo, a_max, para la creación de mapas de peligro por deslizamiento traslacional de laderas inducido por sismo a escala regional en México. Además, se propone utilizar mapas geológicos disponibles para asignar valores promedios de propiedades mecánicas del suelo tales como cohesión, ángulo de fricción, y peso volumétrico y modelos digitales de elevación para estimar la pendiente del talud. Además, se propone emplear ecuaciones de atenuación existentes para estimar a_max dependiendo del tipo de sismo que se desee modelar. Se presenta un mapa de la República Mexicana en donde se muestran las zonas de mayor peligro de deslizamientos para la a_max asociadas a un periodo de retorno de 150 años. Finalmente, se presenta un ejemplo de obtención de un mapa de deslizamiento de laderas inducido por sismo en México: el caso del sismo de Tecomán en Colima de M=7.6 ocurrido el 21 de enero de 2003 y se compara con el obtenido a través del método de Mora-Vahrson.

 

SITIOS Y EVENTOS USADOS

Para definir una expresión para estimar DN en términos de la relación a_c/a_max, es necesario contar con registros de eventos sísmicos. Para ello, se revisaron y seleccionaron las componentes horizontales de los acelerogramas registrados en México debido a sismos de subducción y de falla normal. Los sismos seleccionados tienen magnitudes de entre 5 y 8.1 y aceleraciones máximas del suelo que van de 20 a 402.9 cm/s². Esta última se registró durante el evento en Manzanillo, Colima, el 19 de octubre 1995. En la tabla 1 se presentan los eventos sísmicos que se usaron en este estudio donde se indica la fecha, tipo de sismo, magnitud, localización epicentral y el número de registros usados.

En la figura 1 se muestra la distribución de los eventos sísmicos que se usaron en este estudio (círculos y cuadrados corresponden a sismos de subducción y falla normal, respectivamente). Asimismo, se indican las estaciones acelerométricas (triángulos) desplantadas en sitios de roca en campo libre usadas en este trabajo. De estos registros se leyó directamente el valor de a_max, y se estimó el parámetro D_N como se indica más adelante.

Adicionalmente, la figura 2 muestra la distribución magnitud-distancia de los datos de los 703 registros empleados: 453 y 250 de sismos de subducción y falla normal, respectivamente, obtenidos de 55 estaciones localizadas a distancias entre 3 y 350 km de la zona epicentral. A cada uno de los registros empleados se les corrigió la línea base y se les aplicó un filtro pasabanda entre 0.1 y 10 Hz. Esto proporciona una idea del ajuste esperado de la regresión del parámetro de desplazamiento de Newmark, D_N, que se describe en la siguiente sección.

 

DESPLAZAMIENTO DE NEWMARK, D_N

Para aplicar el método de Newmark se requiere la caracterización de dos elementos: (1) la estabilidad dinámica del talud que será analizado y (2) el movimiento sísmico al que éste estará sujeto.

Estabilidad dinámica del talud

La estabilidad dinámica de un talud se cuantifica por medio de la aceleración crítica (o permisible) a_c. Ésta es el umbral de aceleración del suelo necesaria para superar la resistencia de deslizamiento basal e iniciar un movimiento permanente del talud. La a_c está dada por

donde a_c está en términos de la aceleración de la gravedad (g), α es la pendiente del terreno medida desde la horizontal de la superficie de deslizamiento y FS es el factor de seguridad estático definido como la relación de resistencia entre las fuerzas o momentos en un talud; este, a su vez, se define con base en las propiedades geotécnicas y topográficas del sitio en estudio como

donde Φ>' es el ángulo de fricción efectivo, c' es la cohesión efectiva, γ es el peso específico del material, γ_w es el peso específico del agua, t es el espesor de material medido perpendicularmente al plano de falla, m es el factor de saturación del material y α es el ángulo del talud. Esta ecuación se divide en tres términos, el primero es la componente cohesiva de la resistencia, el segundo es la componente friccionante y el tercer término toma en cuenta la disminución de la resistencia debido a la presión de poro (Luzi et al., 2000). Sin embargo, un parámetro de suma importancia en la estabilidad del talud es el valor de α por lo que las propiedades mecánicas del suelo están ponderadas respecto a éste. Nótese que el valor de a_c (ec. 1) debe ser mayor que cero para ser un talud estable y que resista un nivel de intensidad sin fallar.

Movimientos sísmicos que inducen deslizamientos

Newmark (1965) analizó pulsos de aceleración rectangulares para producir algunas generalizaciones gráficas que se podrían usar para estimar el desplazamiento como función de la relación existente entre a_c y a_max, posteriormente se emplearon métodos similares para refinar estas estimaciones usando una variedad de formas para pulsos de aceleración (triangular y senoidal) así como una gran colección de registros de movimientos fuertes de suelo (Sarma, 1975; Franklin y Chan, 1977; Yegian et al., 1991). Ambraseys y Menu (1988) proponen varias ecuaciones de regresión para estimar D_N mediante un análisis de 50 registros de movimiento fuerte de once sismos. Otros estudios han propuesto ecuaciones de regresión de diferentes formas para estimar el parámetro de desplazamiento de Newmark (Yegian et al., 1991). Una deducción empírica de D_N podría llevar a una estimación simple de la estabilidad del talud, sin embargo, como se indica más adelante, estas ecuaciones realizadas para otras partes del mundo podrían aumentar la dispersión de la estimación de los desplazamientos al ser aplicadas en México dadas las condiciones de sismicidad del país. Por ello, se utilizó una base de datos de sismos mexicanos que permita obtener una mejor correlación entre el parámetro D_N y la relación de la aceleración crítica, a_c, y la aceleración máxima del suelo, a_max, como se detalla más adelante.

El parámetro Dn se obtiene como:

donde a(t) es la aceleración del suelo para cada instante t, T_d es la duración del registro y H es la función de Heaviside (Newmark, 1965).

En la figura 3 se presenta como ejemplo el caso del registro obtenido de la estación CALE del sismo del 19 de septiembre de 1985 componente este-oeste; asumiendo una aceleración crítica a_c=0.02g, indicada con línea punteada (figura 3a); además, se observa el comportamiento de la velocidad relativa, v_rel, entre la masa deslizante y la base del talud una vez que la aceleración relativa llega a cero en cada lapso de deslizamiento (figura 3b) con lo que se obtiene un desplazamiento de la masa deslizante de D_N = 18 cm (figura 3c).

Regresión propuesta para la estimación de D_N

Para los sitios mostrados en la figura 1 se obtuvo la relación a_c/a_max y el parámetro D_N para movimientos sísmicos registrados de sismos de subducción y falla normal en ambas direcciones horizontales. La separación de movimientos sísmicos de acuerdo al origen del sismo es debido a que se observaron diferencias en los resultados. Se asumieron valores de a_c de 0.02 a 0.4 g, que son valores de interés para problemas de estabilidad de taludes propuestos por Jibson (2007).

En la figura 4 se presenta la dependencia de D_N con respecto a la relación entre la aceleración crítica y aceleración máxima del suelo, a_c/a_max, para sismos de subducción y falla normal, arriba y abajo, respectivamente, y la ecuación que mejor se ajusta. Se encontró que el parámetro D_N para sismos de tipo subducción puede estimarse como

donde D_N está en centímetros y ε es un término de error aleatorio, asumido con distribución normal con media igual a 1.04. En el ajuste se obtuvo un coeficiente de correlación de 0.93, por lo que consideramos que el error que se comete en la estimación del parámetro D_N dada la relación a_c/a_max es aceptable.

Para sismos de falla normal se estimó el siguiente ajuste

con un valor de ε igual a 1.22 y coeficiente de correlación de 0.92.

La expresión es válida para el intervalo 0 < a_c/a_max < 1; esto significa que a_c toma valores entre 0 < a_c < a_max . Si a_c ≥ a_max significa que el desplazamiento D_N ≈ 0. La estimación del parámetro D_N no está libre de incertidumbres. Como es bien conocido, estas incertidumbres son factores clave para el análisis de peligro desde un punto de vista probabilista que deben ser consideradas y son comúnmente descritas por la desviación estándar. En la figura 5 se presenta la frecuencia y distribución de probabilidad normal de lnD_N dada la ocurrencia de los dos tipos de sismos estudiados en este trabajo.

 

INFORMACIÓN GEOLÓGICA GEORREFERENCIADA DISPONIBLE

El principal problema que se tiene para estudiar las amenazas geológicas es la falta de información detallada en el sitio de interés. Sin embargo, con la información disponible, es posible tener estimaciones aproximadas que ayuden a identificar zonas de alto peligro y desarrollar allí, si existen recursos, estudios de campo específicos para recabar información más completa y por lo tanto realizar estudios más detallados. Hoy está disponible información geológica (INEGI, 2010) con la cual se pueden asignar, a partir de información disponible en la literatura, las características dinámicas del suelo y poder así usar el método de Newmark. En figura 6 se presenta el mapa de las características litológicas empleadas, obtenidas a partir de agrupar la información geológica disponible, tomando en cuenta similitudes geomecánicas y estructurales de los materiales, escala 1:1'000,000. En la misma figura 6 se presenta la ubicación de los diferentes sitios disponibles (puntos) donde se han realizado sondeos para obtener propiedades geotécnicas de diferentes entidades y publicadas por la Sociedad Mexicana de Ingeniería Geotécnica (antes SMMS). En el Anexo del presente trabajo se indica la ubicación y propiedades geotécnicas resultado de la revisión de esta literatura.

Los valores de resistencia de los geomateriales, caracterizada generalmente por el ángulo de fricción y la cohesión, ya sea en estado seco o saturado, llegan a presentar mucha diferencia incluso dentro de una misma unidad litológica. Asignar valores representativos a los materiales generalmente conlleva una gran incertidumbre, sobre todo si se trata de modelar deslizamientos en áreas extensas. Los valores de resistencia, aún cuando sean derivados de sondeos, resultan difíciles de extrapolar para todo un grupo litológico extenso, dado que son puntuales y dependen del tipo y condiciones del ensayo, de características locales (grado de alteración, presencia de hidrotermalismo, grado de cementación, fracturamiento entre otros). Por ello, para modelar la amenaza por deslizamiento, ya sea inducido por sismo o lluvia, es necesario considerar valores de resistencia promedio representativos de los materiales de la capa de suelo que se encuentra alterada (principalmente de las discontinuidades que representan las zonas de debilidad con la superficie de suelo en contacto con la parte sana del suelo y donde se asume que se presenta el deslizamiento traslacional) debido a la imposibilidad de contar con valores exactos para todas las formaciones rocosas, dadas las limitaciones en cuanto a información, la variabilidad de las propiedades incluso dentro de un mismo afloramiento además de que la escala de trabajo es a nivel regional. En la tabla 2 se presentan valores promedio de propiedades mecánicas de suelo representativos de cada grupo litológico usados para los fines de este estudio (peso específico, γ, cohesión, c', y ángulo de fricción, Φ'; los valores son compilados por diversos autores (Barton, 1974; Hoek y Bray, 1981; Suárez, 1998; Jibson et al., 2000; González et al., 2002) a fin de contar con una referencia general para asignar propiedades a los materiales; así como de estudios de mecánica de suelos disponibles en México. Se presenta además un valor umbral de pendiente en grados para estimar un mecanismo de falla traslacional a partir del cual si se rebasa, se considera se presenta un proceso de remoción diferente al considerado. Esto se basa en el hecho de que, en general, se considera que valores altos de pendiente (>50°-60°) están asociados a zonas con procesos de remoción tales como volteo y desprendimiento de rocas (Suárez, 1998; González et al., 2002); pendientes medias (20-50°) están asociadas a caídas por rodamiento, deslizamientos, reptaciones y pendientes menores (<20°) a solifluxión, creep y flujos.

Para obtener el perfil topográfico, está disponible también el mapa de elevación digital del terreno (INEGI, 2010) del que es posible obtener la pendiente del terreno como más adelante se explica.

De acuerdo a lo anterior, en este trabajo se utilizó la información de la litología georreferenciada del país así como tablas de resistencia basadas en la literatura técnica. Se asignaron valores de cohesión (c'), del ángulo de fricción (Φ') y del peso volumétrico (γ) representativos de cada grupo litológico (González et al., 2002; Hoek y Bray, 1981). En la figura 7 se presentan los valores de cohesión, fricción, peso volumétrico asignados acorde a la tabla 2; así como el perfil de la topografía (empleada en el cálculo de α) de las distintas formaciones rocosas del país integradas dentro de un SIG.

Cálculo del ángulo del talud

El cálculo de la pendiente del terreno es otro de los parámetros de suma importancia en la estimación de los desplazamientos traslacionales. En este artículo, el cálculo del ángulo del talud se llevó a cabo empleando modelos digitales de elevación del terreno con una resolución a cada 30 m. Para cada punto de la malla del modelo digital de elevación (punto base), se calculó la pendiente del terreno en cuatro direcciones: norte, sur, este y oeste. La expresión empleada para el cálculo en grados es dada por

donde α es la ángulo del talud; z₂ es la elevación del terreno en el modelo digital para el punto en la dirección de análisis; z₁ es la elevación del terreno en el modelo digital para el punto base en que se desea calcular la pendiente y Δx es el valor absoluto de la distancia horizontal entre el punto base y el punto en la dirección analizada. El valor del ángulo del talud empleado, corresponde al máximo valor de las cuatro direcciones analizadas.

Relaciones de atenuación sísmica empleadas

Las ecs. 4 y 5, junto con alguna ley de atenuación de la aceleración máxima del suelo permiten realizar mapas de peligro por deslizamiento traslacional de laderas inducido por sismo a nivel regional.

En este trabajo se clasifican los tipos de sismos que puede generar cada fuente sísmica en cuatro grupos: subducción o interplaca, profundidad intermedia, transcurrentes y someros. Para cada uno de estos tipos de sismo está asociada una ley de atenuación diferente según se describe a continuación:

• Temblores interplaca. Para la aceleración máxima del terreno provocada por temblores generados en la costa sur del Pacífico, se utiliza la ley de atenuación de Arroyo et al. (2010). Esta ley fue construida a partir de numerosos registros de aceleración obtenidos por la red acelerográfica de Guerrero, que incluyen los del sismo del 19 de septiembre de 1985.

• Temblores de profundidad intermedia. Se emplea en este caso un modelo de atenuación desarrollado por García et al. (2005). Este fue construido de 16 sismos con magnitudes que se encuentran entre 5.2 y 7.4 y profundidades entre 35 y 138 km.

• Temblores de tipo transcurrente y superficiales. Para modelar la atenuación de los temblores superficiales, tanto los que ocurren en el Eje Neovolcánico como los que se presentan en la parte noroeste del país, se utilizan leyes de atenuación construidas con datos registrados en California (Abrahamson y Silva, 1997).

En la figura 8 se presenta los valores de aceleración máxima del suelo, a_max, asociadas a un periodo de retorno de 150 años. Para ello se usó el programa CRISIS 2007 desarrollado por Ordaz et al. (2007) que emplea parámetros de sismicidad y modelos de fuentes sismogénicas obtenidos de la sismicidad histórica registrada, los cuales cubren la totalidad de la República Mexicana conservando las condiciones de sismicidad generales y su variación regional.

Aceleración crítica

En la figura 9 se presenta la estabilidad del talud calculada por medio de la aceleración crítica (ec. 1). Se puede observar que las zonas que requieren una menor aceleración para generar un desplazamiento traslacional coinciden con las zonas montañosas, con topografía abrupta, y humedad importante que pueden ser detonadas durante un sismo. Sin embargo, aun cuando en el norte del país existen zonas identificadas con problemas de inestabilidad, debido a la baja sismicidad existente (figura 8) podría no presentarse deslizamiento inducido por sismo.

Con esta información y con el modelo de estimación de D_N propuesto en este trabajo, se obtuvo el mapa de deslizamientos potenciales en la República Mexicana (figura 10) considerando como amenaza sísmica las aceleraciones del suelo que tienen un periodo de retorno de 150 años. En la figura 10 también se muestra la localización de municipios donde se han reportado deslizamientos usando información tanto de información histórica como técnica (p.e. Rodríguez et al. 1999; Bommer y Rodríguez, 2002; Alcántara-Ayala, 2008). Nótese en la figura 10 que los deslizamientos potenciales obtenidos a escala regional son una buena aproximación con las áreas reportadas a nivel municipio donde han ocurrido deslizamientos inducido por sismo; resaltando principalmente los estados de Baja California, Sonora, Jalisco, Colima, Michoacán, Guerrero, Estado de México, Puebla, Veracruz, Oaxaca y Chiapas debido a un mayor peligro sísmico, la topografía abrupta y posible importante humedad como antes se mencionó. Es adecuado indicar que la falla en suelos cohesivos es primordialmente rotacional y en suelos puramente friccionantes es plana. Si se tienen suelos cohesivos-friccionantes la falla primordial es rotacional, sin embargo, es posible que para este tipo de suelos se presente algún otro tipo de mecanismo de falla. La figura 10 se debe considerar solamente como una primera aproximación de inestabilidad de taludes con mecanismo de falla plana; otros tipos de inestabilidad como los observados en taludes de carreteras, son debidos al inadecuado diseño del talud en condiciones estáticas o a que estos taludes se localizan en una zona de subsidencia, por lo que el sismo en estos casos, es solamente una componente adicional a la inestabilidad. Este mapa puede ser usado para ubicar zonas en donde se requieren estudios más exhaustivos, y por lo tanto, una mejor asignación de recursos para identificar el potencial de deslizamiento inducido por sismo y poder establecer medidas de mitigación en los bienes expuestos.

 

EJEMPLO DE APLICACIÓN: MAPA DE DESLIZAMIENTO DE LADERAS INDUCIDO POR EL SISMO DEL 21 DE ENERO DE 2003 EN COLIMA

A continuación se presenta un ejemplo de la obtención del mapa de deslizamiento de laderas inducido por sismo para la región afectada por el sismo del 21 de enero de 2003 de magnitud M=7.6. Este evento provocó daños severos en la infraestructura portuaria, daños en el sistema de riego local y partes del sector ferroviario. También durante el evento se presentaron efectos de licuación y detonó numerosos deslizamientos y caídas de rocas: (1) deslizamientos ocurrieron a lo largo de los cañones y barrancas en el norte de Colima debido a que se tienen laderas muy escarpadas con pendientes del orden de 70°, constituidas por materiales de origen volcánicos, intercalados con depósitos fluviales con poca cementación (SMIS y EERI, 2006); (2) otros deslizamientos ocurrieron en barrancas al oriente del Nevado de Colima, donde se presentaron flujos de suelo y rocas, así como caídos y desprendimientos de materiales volcánicos expuestos en las laderas de los cañones; presentándose una concentración de hasta 40 deslizamientos por kilómetro lineal (Wartman et al. 2003) y (3) otros deslizamientos reportados como ligeros fueron en cortes de caminos y carreteras del estado en materiales arenosos y conglomerados andesíticos debido al intemperismo del corte acrecentado por deficiencias o daños al drenaje superficial (Keefer et al. 2006; SMIS y EERI, 2006).

En las figuras 11 y 12 se muestran los resultados de la metodología propuesta por Mora y Vahrson (1993) y la estimada a través de la ec. 4, respectivamente. En las figuras se indican con un sombreado más intenso las zonas más susceptibles a presentar deslizamientos hasta llegar a aquellas a zonas en las que se considera que no existirán deslizamientos (sin sombreado). El método de Mora-Vahrson clasifica la susceptibilidad de deslizamiento de manera cualitativa en un intervalo de 0 a 250, que son los límites superiores e inferiores, respectivamente; en la figura 11 el máximo valor obtenido fue de 90. Por otro lado, también se presenta el levantamiento realizado por Keefer et al. (2006) de puntos locales de deslizamientos (puntos negros) y las regiones de deslizamientos intensos (áreas segmentadas) provocados por el sismo, lo que nos permite comparar con los resultados obtenidos del modelo utilizado y la ec. 4. De estos mapas se pueden hacer las siguientes observaciones:

• Los resultados obtenidos con el método que emplea deslizamientos de Newmark (ec. 4) identifican algunas regiones de deslizamientos que se presentaron durante el sismo de 2003 y que están documentados por Keefer et al. (2006). Sin embargo, se observa que la correlación es baja entre lo ocurrido y lo obtenido (ec. 4) debido a: (1) el método de Newmark no identifica otro tipo de mecanismo de falla (caída de rocas, flujos de detritos, deslizamientos rotacionales), (2) la incertidumbre asociada con la asignación de los parámetros geotécnicos empleados, (3) el método de Newmark no considera los efectos de directividad del sismo y (4) la incertidumbre debida al modelo sísmico empleado (Ordaz et al. 2007).

• El método propuesto cuenta con la información topográfica disponible cuya resolución no permite capturar cambios bruscos del terreno, como es el caso de cortes en carreteras. Por ello, algunos deslizamientos reportados durante el sismo no fueron estimados.

• El Método de Mora-Vahrson sobreestima las regiones donde podrían presentarse deslizamientos.

Los resultados generados en este trabajo son de índole probabilístico y constituyen sólo indicaciones de los posibles resultados de eventos de deslizamiento traslacional de laderas a nivel regional inducido por sismo en el país. De manera que los resultados no constituyen predicciones ciertas de un futuro dictado por resultados predecibles de eventos catastróficos de esta naturaleza. Sin embargo, aún con las limitaciones e incertidumbre que el modelo de deslizamiento empleado puede presentar, éste representa una adecuada herramienta para medir el impacto de un fenómeno natural como el analizado en este trabajo.

 

CONCLUSIONES

Se presenta una expresión para estimar el desplazamiento de Newmark (D_N) en México en términos de la relación entre la aceleración critica, a_c, y la aceleración máxima del suelo, a_max, y se obtuvo una desviación de 1.04 y 1.22 y un coeficiente de correlación de ρ = 0.93 y 0.92 para sismos de subducción y falla normal, respectivamente. Con los resultados que se obtienen de la ecuación de desplazamiento propuesta es posible definir un mapa de peligro sísmico por deslizamiento traslacional de laderas inducido por sismo a nivel regional. Para ello se propone utilizar la información de los mapas geológicos a escala 1:1'000,000 y asignar valores promedio de cohesión, peso volumétrico y ángulo de fricción a partir de información disponible en la literatura y estudios de mecánica de suelo disponibles, además de asignar la pendiente topográfica a partir de los mapas de elevación digital del terreno. Con base en estos cálculos se presentan mapas de la República Mexicana de aceleración crítica y desplazamientos traslacionales potenciales del suelo para un periodo de retorno de 150 años de aceleración del suelo. Además, se presentan mapas de desplazamientos traslacionales en laderas expresado en términos del desplazamiento de Newmark y mapas de susceptibilidad obtenidos con el método Mora-Vahrson para el sismo del 21 de enero de 2003 ocurrido en la región de Colima.

Se muestra que es posible obtener mapas a nivel regional de desplazamientos de laderas para identificar zonas de alto peligro de inestabilidad de taludes, lo que permite canalizar recursos en la elaboración de estudios más detallados que coadyuven a tomar medidas de prevención. Debido a las limitaciones del método usado, los resultados obtenidos consideran únicamente la inestabilidad de taludes con falla plana.

Una de las aplicaciones potenciales de este tipo de mapas se encuentra en la estimación de pérdidas esperadas en bienes expuestos por la ocurrencia de deslizamiento de laderas a nivel regional que se pudieran presentar ante la ocurrencia de un evento sísmico. Además, la aplicación de la metodología presentada es de importancia en la planeación del uso de suelo, desarrollo urbano, particularmente para regiones donde han ocurrido deslizamientos inducidos por sismo y se cuenta con escasos o nulos estudios geotécnicos.

 

AGRADECIMIENTOS

Se agradece al Dr. Víctor Carlos Valerio el apoyo en la elaboración de mapas temáticos y a la Secretaría de Hacienda en el financiamiento del proyecto "Integración, análisis y medición de riesgo de sismo, inundación y ciclón tropical en México para establecer los mecanismos financieros eficientes de protección al patrimonio del fideicomiso FONDEN del Banco Nacional de Obras y Servicios Públicos (BANOBRAS)". Agradecemos las observaciones por parte de los revisores anónimos que mejoraron y enriquecieron la calidad del artículo.

 

REFERENCIAS

Abrahamson, N. y Silva W. (1997), "Empirical response spectral attenuation relations for shallow crustal earthquakes", Seismological Research Letters, Vol. 68, No. 1, pp. 94-127.         [ Links ]

Alcántara-Ayala, I. (2008), "On the historical account of disastrous landslides in Mexico: the challenge of risk management and disaster prevention", Adv. Geosci., Vol. 14, pp. 159-164.         [ Links ]

Alcántara-Ayala, I., Esteban-Chávez, O. y Parrot J.F. (2006), "Landsliding related to land-cover change: A diachronic analysis of hillslope instability distribution in the Sierra Norte, Puebla, Mexico", Catena, Vol. 65, No. 2, pp. 152-165.         [ Links ]

Ambraseys, N.N. y Menu, J.M. (1988), "Earthquake-induced ground displacements", Earthquake Engineering and Structural Dynamics, Vol. 16, No. 7, pp. 985-1006.         [ Links ]

Arroyo, D., García, D., Ordaz, M., Alexander, M. y Singh, S.H. (2010), "Strong ground-motion relations for Mexican interplate earthquakes", Journal of Seismology, Vol. 14, pp. 769-785.         [ Links ]

Barton, N.R. (1974), "A review of the shear strength of filled discontinuities in rock", Norwegian Geotech. Inst. Publ. No. 105. Oslo: Norwegian Geotech. Inst.         [ Links ]

Bommer J., Rodriguez C. (2002), "Earthquake-induced landslides in Central America", Engineering Geology, Vol. 63, No. 3-4, pp. 189-220.         [ Links ]

Del Gaudio, V. y Wasowski, J. (2004), "Time probabilistic evaluation of seismically-induced landslide hazard in Irpinia (Southern Italy)", Soil Dynamics and Earthquake Engineering, Vol. 24, No. 12, pp. 915-928.         [ Links ]

Franklin, A. y Chang, F. (1977), "Earthquake resistance of earth and rock-fill dams", US Army Corps of Engineers Waterways Experiment Station, Vol. S-71-17.         [ Links ]

García, D., Singh, S.H., Herráiz, M., Ordaz, M. y Pacheco, J.F. (2005), "Inslab earthquakes of Central Mexico: peak ground-motion parameters and response spectra", Bulletin of the Seismological Society of America, Vol. 95, No. 6, pp. 2272-2282.         [ Links ]

González, L., Ferrer, M., Ortuño, L. y Oteo, C. (2002), "Ingeniería geológica", Prentice Hall, Pearson Education, Madrid, 715 p.         [ Links ]

Hoek, E. y Bray, J. W. (1981), "Rock slope engineering", Institution of Mining and Metallurgy, 3a edición, 358 p.         [ Links ]

INEGI (2010). http://www.inegi.org.mx/geo/contenidos/recnat/geologia/default.aspx        [ Links ]

Jibson, R.W. (1993), "Predicting earthquake-induced landslide displacements using Newmark's sliding block analysis", Transportation Research Record, 1411, pp. 9-17.         [ Links ]

Jibson, R.W., Harp, E.L. y Michael, J.M. (1998), "A method for producing digital probabilistic seismic landslide hazard maps: an example from the Los Angeles, California area". US Geological Survey Open-File Report, pp. 98-113.         [ Links ]

Jibson, R.W., Harp, E.L. y Michael, J.M. (2000), "A method for producing digital probabilistic seismic landslide hazard maps", Engineering Geology, Vol. 58, No. 3-4, pp. 271-289.         [ Links ]

Jibson, R. (2007), "Regression models for estimating coseismic landslide displacement", Engineering Geology, Vol. 91, pp. 209-218.         [ Links ]

Keefer, D., Wartman, J., Navarro, O., Rodriguez-Marek, A. y Wieczorek, G. (2006), "Landslides caused by the M 7.6 Tecomán, Mexico earthquake of January 21, 2003", Engineering Geology, Vol. 86, pp.183-197.         [ Links ]

Luzi, L., Pergalani, F. y Terlien, M.T.J. (2000), "Slope vulnerability to earthquakes at subregional scale, using probabilistic techniques and geographic information systems", Engineering Geology, Vol. 58, No. 3-4, pp. 313-336.         [ Links ]

Mankelow, J.M. y Murphy, W. (1998), "Using GIS in the probabilistic assessment of earthquake triggered landslide hazards", Journal of Earthquake Engineering, Vol. 2, pp. 593-623.         [ Links ]

Miles, S.B. y Keefer, D.K. (2000), "Evaluation of seismic slope performance models using a regional case study", Environmental & Engineering Geoscience, Vol. 6, pp. 25-39.         [ Links ]

Miles, S.B. y Keefer, D.K. (2001), "Seismic landslide hazard for the city of Berkeley, California", US Geological Survey Miscellaneous Field Studies Map, MF-2378.         [ Links ]

Mora, S. y Vahrson, W.G. (1993). "Determinación a-priori de la amenaza de deslizamientos en grandes áreas utilizando indicadores morfodinámicos", Tecnología ICE, Vol. 3, No. 1, pp. 32-42.         [ Links ]

Mora, S. y Vahrson W.G. (1994), "Macrozonation methodology for landslide hazard determination", Bulletin of the Association of Engineering Geologist, Vol. XXXI, No. 1, pp. 49-58.         [ Links ]

Newmark, N.M. (1965), "Effects of earthquakes on dams and embankments", Géotechnique, Vol. 15, No. 2, pp. 139-160.         [ Links ]

Ordaz, M., Aguilar, A. y Arboleda, J. (2007), CRISIS2007-Ver. 7.2: Program for computing seismic hazard, Instituto de Ingeniería, UNAM, México.         [ Links ]

Rathje, E. y Saygili, G. (2006), "A vector hazard approach for Newmark sliding block analysis", Proceedings, New Zealand Workshop on Geotechnical Earthquake Engineering Workshop, 20-23 noviembre. Universidad de Canterbury, Christchurch, Nueva Zelandia, pp. 205-216.         [ Links ]

Rodríguez, C., Bommer, J. y Chandler, R. (1999), "Earthquake-induced landslides: 1980-1997", Soil Dynamics and Earthquake Engineering, Vol. 18, pp. 325-346.         [ Links ]

Sarma, S.K. (1975), "Seismic stability of earth dams and embankments", Geotechnique, Vol. 25, pp. 743761.         [ Links ]

Sasha, K., Nagai, O., Solidum, R., Yamazaki, Y. y Ohta, H. (2010) "An integrated model simulating the initiation and motion of earthquake and rain induced rapid landslides and its application to the 2006 Leyte landslide," Landslides, Vol. 7, No. 3, 219-236.         [ Links ]

Suárez, D.J. (1998), "Deslizamientos y estabilidad de taludes en zonas tropicales", Instituto de Investigaciones sobre Erosión y Deslizamientos, Colombia, 548 p.         [ Links ]

SMIS y EERI (2006), "El sismo de Tecomán, México del 21 de enero de 2003", Informe de la SMIS y el EERI dentro de la serie "Aprendiendo de los sismos", 291 p.         [ Links ]

Wartman, J. Rodriguez-Marek, A., Keefer, D., Deaton, S., Repetto, P., Macari, E., Navarro, C., Tejeda, J., Silva, C. y Armando, J. (2003), "Preliminary reconnaissance report on geothecnical engineering aspects of the January 21, 2003 Colima Mexico Earthquake", Reporte de la Fundación Nacional de Ciencias en los Estados Unidos de Norteamérica, http://geoinfo.usc.edu/gees/.         [ Links ]

Wieczorek, G.F., Wilson, R.C. y Harp, E.L. (1985), "Map showing slope stability during earthquakes in San Mateo County, California", U.S. Geological Survey Miscellaneous Investigations, Mapa I-1257-E, Escala 1:62,500".         [ Links ] Wilson, R.C. y Keefer, D.K. (1985), "Predicting aerial limits of earthquake-induced landsliding", en J.I. Ziony (ed.), Evaluating earthquake hazards in the Los Angeles region - An Earth-Science Perspective, USGS artículo 1360, pp. 316-345.         [ Links ]

Yegian, M.K., Marciano, E.A. y Ghahraman, V.G. (1991), "Earthquake-induced permanent deformations: probabilistic approach", Journal of Geotechnical Engineering, Vol. 117, No. 1, pp. 35-50.         [ Links ]

 

Nota

* Se aceptarán comentarios y/o discusiones hasta cinco meses después de su publicación.