1. Introduction

The piezoelectric materials have been studied since 1880 when the Curie brothers showed the direct piezoelectric effect. The behavior of these materials in the linear regime is well known and makes accurate predictions, for this reason they are used in a wide range of applications. Currently, the piezoelectric materials are used in DC and radio frequency applications. In DC scope, the most common devices are weight sensors, pressure sensors, static electricity sensors and detectors of a several type of gasses, also, in the resonant applications they are used as resonators, high Q filters, Delay lines, ladder filters, and analog base clock for the modern computers (e.g. crystals used in motherboards).

The piezoelectric materials can be produced from several fabrication processes and the physical deposition as RF magnetron sputtering can bring to the material optimal performance for thin layers, low deposition temperature (below of 200°C) and high chemical resistance ^[1]. These characteristics make them ideal materials for integration in the main manufacturing processes for IC such as CMOS, FD-SOI and FinFET. So, the use of piezoelectric materials also offers low fabrications costs since their fabrication technologies require less photolithographic resolution.

In radio frequency applications the controlled oscillators and active filters are used in a wide range of applications because these devices present a good performance ^[2-3], great integration capability and high resonance frequency presenting two trade-offs, first between their integration capability respect the use of die area and second is between the performance and the power consumption as consequence of the losses associated to the operation frequency and their own power dissipation ^[4-6].

On the other hand, piezoelectric materials can be used in passive devices for radio frequency applications to overcome the aforementioned disadvantages of active devices by offering a high quality factor, low power consumption and easy design techniques. Snyder et al. ^[7] have reviewed multiplexers on substrate integrated waveguides (SIW), mixers, intrinsically switchable filters and band-pass filters, highlighting that in each application the advantages the piezoelectric base material on the performance of the devices.

Up to date, the fifth generation of mobile network (5G) and internet of things (IoT) are technologies demanding great attention because their many fields of application. Among the requirements for useful devices in these technologies are high scalability, high response speed, wide bandwidth and low power consumption ^[8-10]. The piezoelectric resonators are a suitable option due to their high quality factor, low delay time (are analogous devices), easy design techniques, low cost and compatibility with the main standard IC fabrication processes.

For tuning piezoelectric resonant devices, several strategies have been developed for expanding their implementation possibilities. Among the linear techniques for tuning these devices are the use of a variable capacitor for the electrical response modification ^[11], or the induction of a change in mechanical behavior with an external magnetic field through the magnetostrictive piezoelectric materials ^[12]. The use of active devices for tuning piezoelectric resonators also has been used but, the high area consumption and the resulting performance are not enough for the high technology requirements in industrial applications ^[13]. In the literature, it can be found experimental evidence that shows that some nonlinear effects can be used to design tunable piezoelectric devices for achieving the demanding requirements of the high technology. This is done through the change in the effective stiffness behavior due to the presence of a relatively high electric field or the change in the acoustic impedance of the Bragg reflector ^[14]. In this work we present the nonlinear state equations for piezoelectric materials and their use in the design of piezoelectric devices for radio frequency applications that result in a performance that meet the requirements that the current high technology is demanding.

2. Nonlinear state equations

Currently, the modern simulation software uses the stress-charge form to analyze the continuous solid's mechanics, and for this reason we choose build a nonlinear formulation in that representation. Other nonlinear formulations and their mathematical treatment can be found in the literature ^[15,16,17]. Starting from the thermodynamic potential of electric Gibbs function ^[18] and assuming the Einstein and Voigt notation

where G₂, T_λ, S_μ, D_i and E_k are the electric Gibbs function, stress field, deformation field, electric displacement field and the electric field respectively. Then, if we take the total differential respect to the dependent variables we obtain

where Cλμ, ϵij and ekλ are the elasticity constants, the electric permittivity and the piezoelectric coefficients respectively. To derive the nonlinear state equations we expand each coefficient through a Taylor expansion in Eq. (2) assuming that they are function of E_k and S_μ. So for the case of elasticity constants we obtain

Since Eq. (1) is a total differential then we can deduce that

and knowing that G₂ is continuous and has an exact differential we can assume that G₂ has derivatives up to third order. Using these conditions, and the consequences in the symmetry for the indexes (as result of thermodynamic properties of the system) we can define

Finally, we can deduce the nonlinear state equations using (2), (3), (4), (5) and integrating (2) obtaining

where

The theoretical procedure implies that one needs not an algebraic factor between the Voigt and original tensor representations.

The tλμν tensor represents the nonlinear contribution to the stress field and rijk is the nonlinear contribution to the electric displacement field. The gλμkSμEk is the correction term for the elastic behavior due to the elastoelectric effect and qijλEjSλ is the correction factor for the electric permittivity, both effects take place through a non-linear behavior that appear when a relatively high electric or strong deformation field are applied to the material. The two remaining tensor terms in Eq. (6) are the power balance coupling between the electric and mechanical fields, allowing the total power differential to remain unchanged when the contribution from nonlinear tensors is included.

3. Main nonlinear effects in piezoelectric materials

The nonlinear effects in piezoelectric material appear when the material is subjected to a relatively high electric field and strong deformations. The change in the effective elasticity constants and the raise of a soft ferroelectric effect are the main nonlinear consequences. In this context, the ferroelectric effect produces a hysteresis behavior when a spontaneous polarization or deformation appear in the material, this is produced for mainly two causes, the change of the surface area in domain walls and the alignment of the polar moment within unit cells in the material following the external electric field ^[19]. When the domain walls changes produce a spontaneous strain contributing to the electric displacement field and stress field, and the alignment of polar moments in the unit cells produces a spontaneous polarization field contributing to the strain field. So, a cyclic relation can be measured between the polarization field and deformation field as a function to the electric field resulting in a hysteresis and butterfly loops, respectively ^[20].

The change in the effective elasticity constants appear in the material when the unit cells are subjected to strong deformations since the restoration force within them is not produced only by a mechanical force, then an electrical restoration force contribute to the increasing of the elasticity constants. This elastoelectric effect has the direct consequence of produce a shift in the resonance frequency of the device ^[21], this effect has direct relation with the nonlinear state Eqs. (6) since the effective elasticity constants can be expressed as

and taking into account that the main contribution to the shift is due to the nonlinear behavior produced by the external electric field ^[14], the change in the capacitance of the resonator and the differential of the thickness of the device can be neglected.

The electromechanical coupling factor keff2 is a measurement of the power interchange between the stress field and displacement electrical field, the way to calculate it depends of the specific device geometry, but for the most commonly piezoelectric resonators are given by an expression of the form ^[22-23]

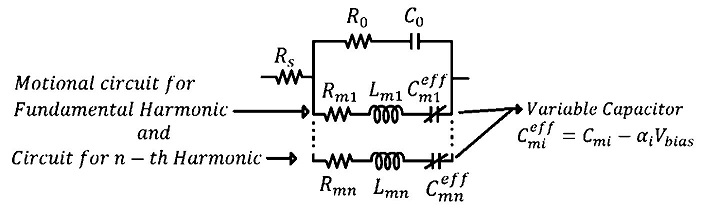
for a wave with x-propagation and a z-shear oscillation mode. The most important variation in Eq. (8) is due to the effective elasticity constants, hence, when a shift of the resonance frequency occurs the electromechanical coupling factor increases meanwhile the effective elasticity constants decreases so, for applications where the effectiveness of the power transduction is the goal (e.g. energy harvesting based on piezoelectric material ^[24]), a negative external electric field can increase this parameter. The equivalent circuit model to include the nonlinear effects described is proposed below. The modified Butterworth Van-Dyke model (mBVD) for piezoelectric resonators has three static lumped elements R_s is the serial resistance, C₀ is the dielectric capacitance and R₀ is the electrode resistance. The modeling of the electromechanical coupling is done through the three motional lumped elements the R_m motional resistance, C_m motional capacitance and L_m motional inductance, these three elements are put for each resonance harmonic of the frequency response of the piezoelectric resonator ^[25].

The proposed model is shown in Fig. 1 where the motional capacitance for each harmonic is variable respect to the external electric field. The effective motional capacitance for the circuit modeling of i-th harmonic Cmieff is calculated as

where C_mi is the motional capacitance without taking into account nonlinear effects, α_i is the fitting parameter and depends on the material and the main oscillation mode of the respective harmonic, finally V_bias is the input offset voltage of the radio frequency signal, since as explained below this is a common and easy technique to take advantage of the nonlinear effects. This change in the mBVD is enough taking into account that the shift of the resonance frequency and the change in the electromechanical coupling have estimated variations around of 2.5% of nominal resonance frequency and up to 0.03, respectively ^[26].

Figure 1 Modified Butterworth Van-Dyke model for equivalent circuit modeling. The variable capacitor allows modeling both, the shift of the resonance frequency and the change in the electromechanical coupling factor. 

4. Nonlinear applications

For applications based on nonlinear effects in piezoelectric materials it is fundamental to determine the symmetry structure of each nonlinear tensor in Eq. (6). For these calculations, we start from these equations and calculate the transformation laws for each tensor, so using the M_αβ and N_γδ matrix defined as in Ref. ^[27], and knowing that every symmetry generators a_ij belongs to the symmetry group of each point group, we calculate the transformation laws getting

and taking into account that each rotated tensor must remain invariant respect to the original tensors (e.g.tλμν'= tλμν), the Eqs. (10) can be solved, to obtain the symmetry structure of each tensor for every crystal system that corresponds to a specific symmetry generator a_ij. All point groups (crystal classes) have the q_ijλ and t_λμv tensors different of zero, and the g_λμk and r_ijk tensors are zero if the material does not exhibit the linear piezoelectric effect, with the exception of the 432 point group, where r_ijk remains equal to zero while g_λμk is not null. The specific symmetry structure of tensors is very large, for this reason in Table I, in order to save space and keep the concept clear, it is only shown the non-zero components of the tensors g_λμk , q_ijλ and r_ijk for α-quartz, β-quartz, PZT in 4 mm phase and aluminum nitride (AlN), since these materials are commonly used at the industrial and research level. The hysteresis behavior discussed in Sec. 3 can be associated to r_ijk and q_ijλ tensors, so the crystal materials where these two tensors remains different from zero can be used in applications where a memory or hysteresis behavior is the main characteristic used in the device. In Ref. ^[28] is shown a brief analysis of r_ijk and t_ijλ in stress-charge formulation, and q_ijλ in strain-charge formulation.

In radio frequency applications, the tunability is a desired capability for devices. The shift of the resonance frequency of piezoelectric resonators is around of 2.5% of nominal frequency through nonlinear effects. This type of resonators can be used in 5G non-standalone (NSA) standard, where the bandwidth requirement is around of 70 MHz. For example, in the 3550-3650 MHz for 5G NSA ^[29]. A piezoelectric resonator can be used to select up to six channels for a full duplex communication through a multiplexing in time and frequency. Within the domestic applications, the circuit for Wi-Fi select channel can be implementing through a piezoelectric resonator with a resonance frequency of 2.4 or 5 GHz to obtain a tuning range of 150 MHz of 300 MHz, respectively, meeting the requirements of bandwidth and number of channels for the standards 802.11n, 802.11ac, etc. Since the piezoelectric resonators have high quality factor, low power consumption and easy design techniques, the whole performance of these devices can be increased by adding surface Bragg reflectors in the same way that the bulk Bragg reflectors actually are used in solidly mounted resonators (SMR) to increase the quality factor, but the SMR performance is decreased mainly by the losses associated to the bulk wave translation. In the Lamb wave resonators (LWR) the oscillation waves of interest are confined to the surface of device where the mentioned losses are no longer present. So the surface Bragg reflectors can be utilized to increase the quality factor. Finally, by adding a rail to bias the surface Bragg reflectors we can induce the tunability desired through nonlinear effects. In Fig. 2 can be seen three different ways to implementing LWR devices where s is the separation between the IDTs and surface Bragg reflector, p is the pitch and h_p is the optimal piezoelectric thickness. These devices result in a high quality factor, low power consumption while using conventional design techniques. The tune capability and their resonance frequency f_r is set by

where ρ is the density of material and λ_d is the wavelength of device.

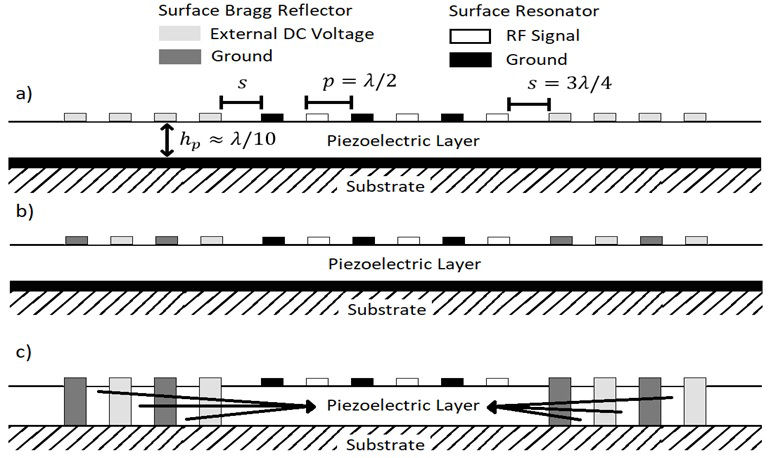
Figure 2 Transversal cut of LWR devices implementing the tunability through nonlinear effects. a) Transversal stress, b) longitudinal stress to the mechanical wave translation and c) longitudinal stress to the mechanical wave translation and optimal Bragg reflector. 

The different implementations for LWR devices shown in Fig. 2 are based on the several ways to induce the nonlinear effects taking into account the possibility of the air gap instead of substrate below of devices. In Fig. 2a) and 2b) the external induced stress is transversal to the mechanical wave translation, whereas in Fig. 2c) the stress is longitudinal to the wave and the last design include a Bragg reflector whose function is to change the medium stress to enhancing the confinement of the mechanical waves within the LWR device.

5. Conclusions

The tunable piezoelectric resonators are a feasible option for modern communications systems where a high quality factor, low power consumption and easy design techniques are required, e.g. in 5G NSA and Internet of Things. Starting from first principles considerations, we present which materials can be used as the tunable resonators, piezoelectric memory devices and energy harvester's applications, and this is summarized in Table I, where the value of the symmetry structure tensor (zero o nonzero), define its application. A novel implementation of conventional Bragg reflector was presented as surface Bragg reflector allowing to get a high quality factor and tune capability in Surface Acoustic Wave (SAW) and LWR devices.