1. Introduction
Since the discovery of the spin at the beginning of the last century [1-3], which was an inflection point and a profound change for semiconductor applications. After some years, a new discipline was created in physics to study electron spin: it is spintronics. The importance of applications of spintronics or magnetoelectronics is store information and the giant magnetoresistance (GMR) for drive head technology [4]. To manufacture the components intended for spintronics, the researchers doped the semiconductor by transition elements, when will later call them DMSs (the dilute magnetic semiconductors). The first DMSs In1−xMnxAs was produced by a molecule beam epitaxy (MBE) [5]. Nevertheless, work has not stopped and is still rising; in the last decade many researchers are working on diluted magnetic III-V and IIVI semiconductors for spintronics applications [6-12]. The magnetic properties of Heusler are calculated by several researchers [13-18]. Researchers and scientists pursue another work line to identify other spintronic components and between these axes the ternaries II-VI and III-V doped with a metallic element [19-20]. The essential intention of this article is to predict the half-metallic property in III-V-N alloy, by doping of transition metal atom manganese, we have chosen the following quaternary BBi 0.75 Mn 0.125 N 0.125 alloy.
2. Calculation details
Developed on full potential linearized augmented plane wave (FP-LAPW) method in accordance with the framework of DFT (density functional theory) [21] electronic structure, half-metallic behavior, and magnetic properties were investigated using WIEN2k code [22-24]. Generalized gradient approximation within Perdew-Burke-Ernzerhof (PBEsol) [25] approximation was employed for exchange-correlation, jointed with the modified Becke-Johnson (mBJ) potential [26] and also spin-orbit coupling (SOC) [27-29] was applied. Boron-Bismuth (BBi) crystallizes in the zincblende structure (no. 216) [27-29]. Its conventional structure has two types of atoms, B and Bi, located at (0,0,0) and (0.25,0.25,0.25) positions, respectively. We create a supercell of 16 atoms, 8 atoms for Boron (B) and 8 for Bismuth (Bi), we substituted one atom of Manganese (Mn), and one atom of Nitrogen (N) at Bismuth (Bi) sites to create BBi 0.75 Mn 0.125 N 0.125 zincblende structure. In this article, we have designed the following calculation parameters: the muffin-tin radii (MT) for B, Bi, Mn, and N to be 1.64, 2.39, 2.29, and 2.13 atomic units (a.u.), respectively. The K max = 9 (RMT)−1 (K max is the plane wave cut-off, and RMT is the smallest of all atomic sphere radii). The Fourier expanded charge density was truncated at G max = 12 (Ryd) 1/2 , the l-expansion of the non-spherical potential and charge density was carried out up to l max = 10. The cut-off energy is set to -6 Ryd to separate the core from valence states. The self-consistent calculations are judged to be converged when the total energy of the system is stable within 10−4 Ryd.
3. Results and discussions
3.1. Phase stability, Structural and elastic properties
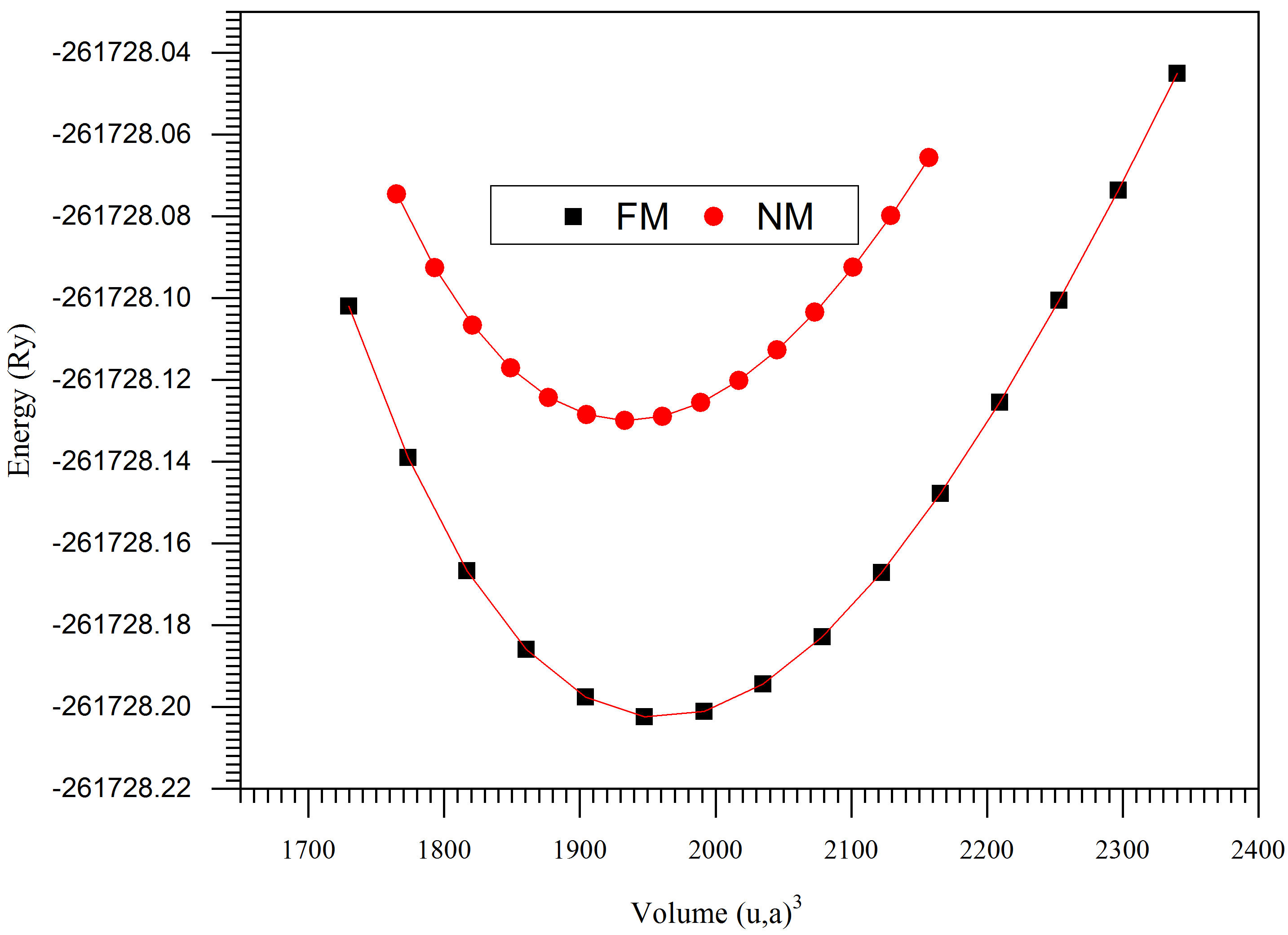
To confirm the phase stability of the structure, we carried out the volume optimization and plotted the energy as a function of the volume for both magnetic and non-magnetic cases. Figure 1 exhibit the energy as a function of the volume. For the ferromagnetic curve localized under to non-magnetic curv, it is concluded that the compound contains the minimum energy in the ferromagnetic phase compared to the non-magnetic phase, which indicates that the BBi 0.75 Mn 0.125 N 0.125 alloy is stable in ferromagnetic phase. The ground-state properties such as the equilibrium lattice constant a, the bulk modulus B 0, the bulk modulus pressure derivative B’, minimum equilibrium energy E 0, and equilibrium volume V 0, are presented in Table I.
TABLE I Calculated lattice constant (α), bulk modulus (B), pressure derivative B’, minimum equilibrium energy E0, and equilibrium volume V0 BBi0.75Mn0.125N0.125.
| α(Å) | B (GPa) | B’ | Energy E0 (Ry) | Volume V0 (a.u3) | Character |
| 10.5096 | 91.3200 | 4.6243 | -261728.202334 | 1961.0587 | Ferromagnetic |
| 10.4686 | 91.4098 | 4.6388 | -261728.130051 | 1935.5166 | Non-magnetic |
The derivative of the energy as a function of the lattice strain is essential for knowing the elastic constants [30]. This strain is picked so that the volume of the unit cell is saved, for the situation of the cubic framework. Along these lines, for the figuring of flexible constants: C 11, C 12, and C 44, we have utilized the Mehl strategy [31], Following this technique, we determined the shear modulus C 11 − C 12 from the volumepreserving orthorhombic strain tensor:
Utilization of this strain changes the total energy from its unstrained value to:
Where V 0 is the volume of the unstrained equilibrium unit cell, and E(0) is its total energy. For the elastic constant C 44, we used a volume-conserving monoclinic tensor.
Which changes the total energy to:
For isotropic cubic crystal, the bulk modulus B is given by:
The Young’s modulus E, shear modulus G, and Lame’s coefficients (µ and λ) can be derived from the elastic constants, using the following standard relations:
Similarly, the Poisson coefficient (σ) provides information on the ductility or fragility of the materials and is expressed as follows:
The anisotropy factor is given by the following equation:
Stability criteria for cubic crystals require [32]:
These conditions in our study are satisfying, and the structure is therefore mechanically stable. The calculated values of the elastic constants (C 11, C 12 and, C 44), shear modulus G, Young’s modulus E, the anisotropy A, Poisson’s ratio σ, and Lame’s coefficients (µ and λ) are given in Table II.
TABLE II The calculated elastic constants of the BBi0:75Mn0:125N0:125
| C11 | 143.008 (GPa) |
| C12 | 65.375 (GPa) |
| 4C44 | 102.444 (GPa) |
| B | 91.252 (GPa) |
| GV | 76.993 (GPa) |
| GR | 61.874 (GPa) |
| GH | 69.433 (GPa) |
| E | 166.158 (GPa) |
| B/G | 1.314 |
| A | 2.639 |
| σ | 0.196 |
| µ | 69.433 (GPa) |
| λ | 44.963 (GPa) |
| vt | 2936.280 (m/s) |
| vl | 4777.730 (m/s) |
| vm | 3240.400 (m/s) |
| θD | 367.017 (K) |
Acquiring calculated Young’s modulus E, bulk modulus B, and shear modulus G, one can estimate the Debye temperature, which is an important fundamental parameter closely related to many physical properties such as elastic constants, specific heat, and melting temperature. One of the main technique to predict the Debye temperature (θ D ) is from elastic constants data, since θ D may be estimated from the average sound velocity, v m by the following expression [33]:
Where h is Plank’s constant, k B Boltzmann’s constant, and V a is the atomic volume. The standard sound velocity in the polycrystalline material is given by [34]:
where v l and v t are the longitudinal and transverse sound velocity in an isotropic material which can be attained using the shear modulus G and the bulk modulus B from Navier’s formula [35]:
The calculated sound velocity and Debye temperature are given in Table II. However, to our knowledge, there are no data available related to these properties in the literature for these compounds. Pugh [36] propose the ratio B/G, a relationship related to brittle or ductile behavior of materials a high B/G ratio is associated with ductility, whereas a low value corresponds to the brittleness. The critical value separating ductile and brittle material is 1.75; the ratio B/G is 1.314 for BBi 0.75 Mn 0.125 N 0.125 , so the structure is brittle.
3.2. Electronic properties and half-metallic behavior
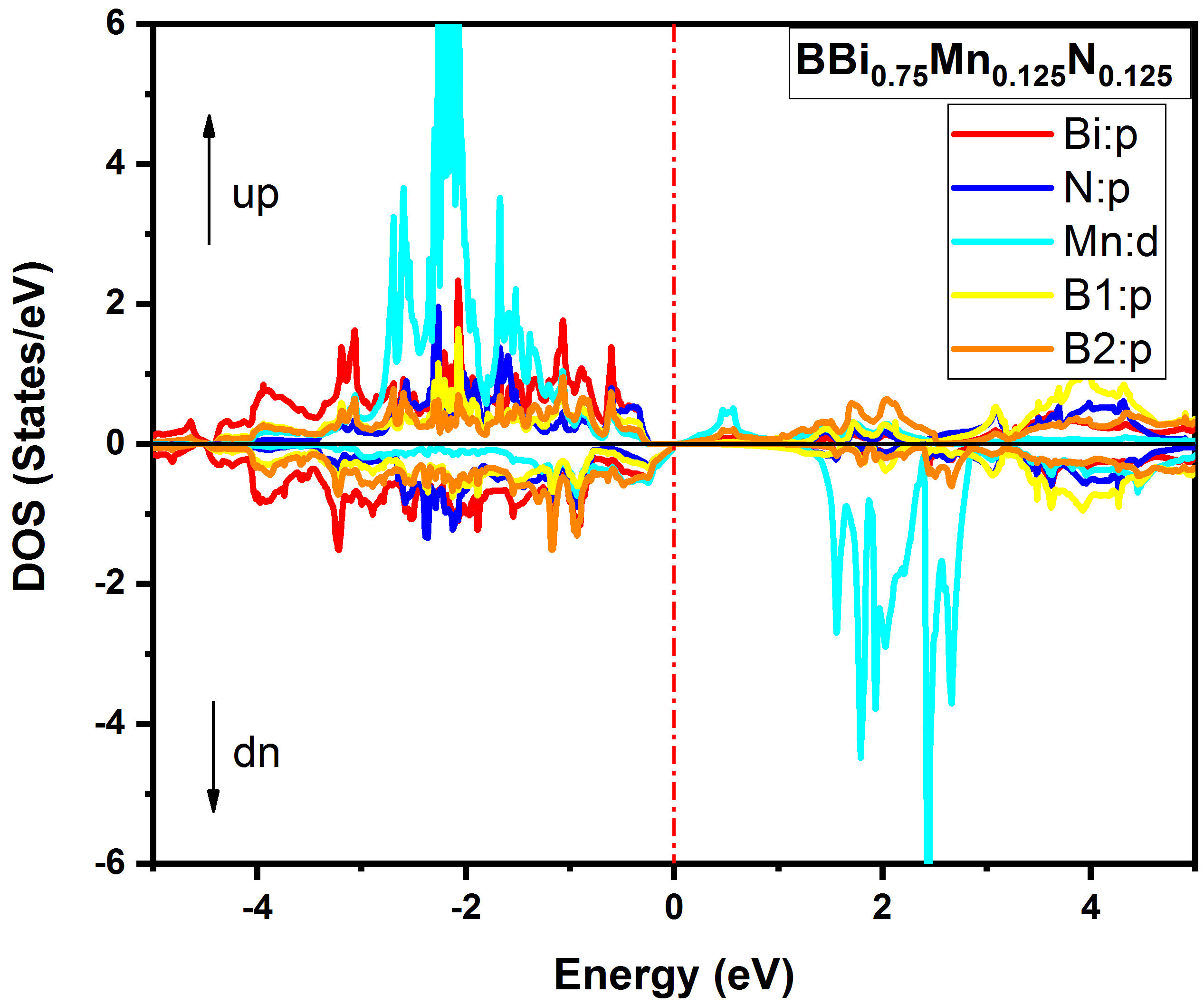
In this part, we present the electronic band structure, total and partial densities of states for BBi 0.75 Mn 0.125 N 0.125 using the GGA-PBEsol and TB-mBJ approaches. Figure 2 exhibits the spin-polarized band structure obtained with TBmBJ for BBi 0.75 Mn 0.125 N 0.125 for majority spin (spin-up). It is observed that the half-metallic gap is seen in the spin-up channel, the indirect bandgap is about 0.25 eV between the Γ and L high symmetry points. Figure 3 shows the band structure for BBi 0.75 Mn 0.125 N 0.125 for minority spin (spin down), it is clear that the maximum of the valence band is above the Fermi level, therefore the structure has metallic behavior. The total (T) and partial (P) electron densities of states of BBi 0.75 Mn 0.125 N 0.125 are shown in Fig. 4 and Fig. 5, respectively. Figure 3 shows that BBi 0.75 Mn 0.125 N 0.125 compound present half-metallic ferromagnetic comportment as the density of states (DOS) passes Fermi level in the spindown version, and it is also clear from the figure that the peaks around -1.8 eV are mainly contributed by the total density states of Mn. The partial density of states (PDOS) of BBi 0.75 Mn 0.125 N 0.125 is presented in Fig. 4, and it is more apparent that 3d states of Mn largely implicated in the peaks around -1.81 and 2.80 eV. The energy gap is acquired resulting from the hybridization of the 3d-state of Mn, p-state of Bi, and p state of N, as shown in Fig. 4. The half-metallic ferromagnetic behavior of BBi 0.75 Mn 0.125 N 0.125 imply applications of the structure in the spintronic devices.
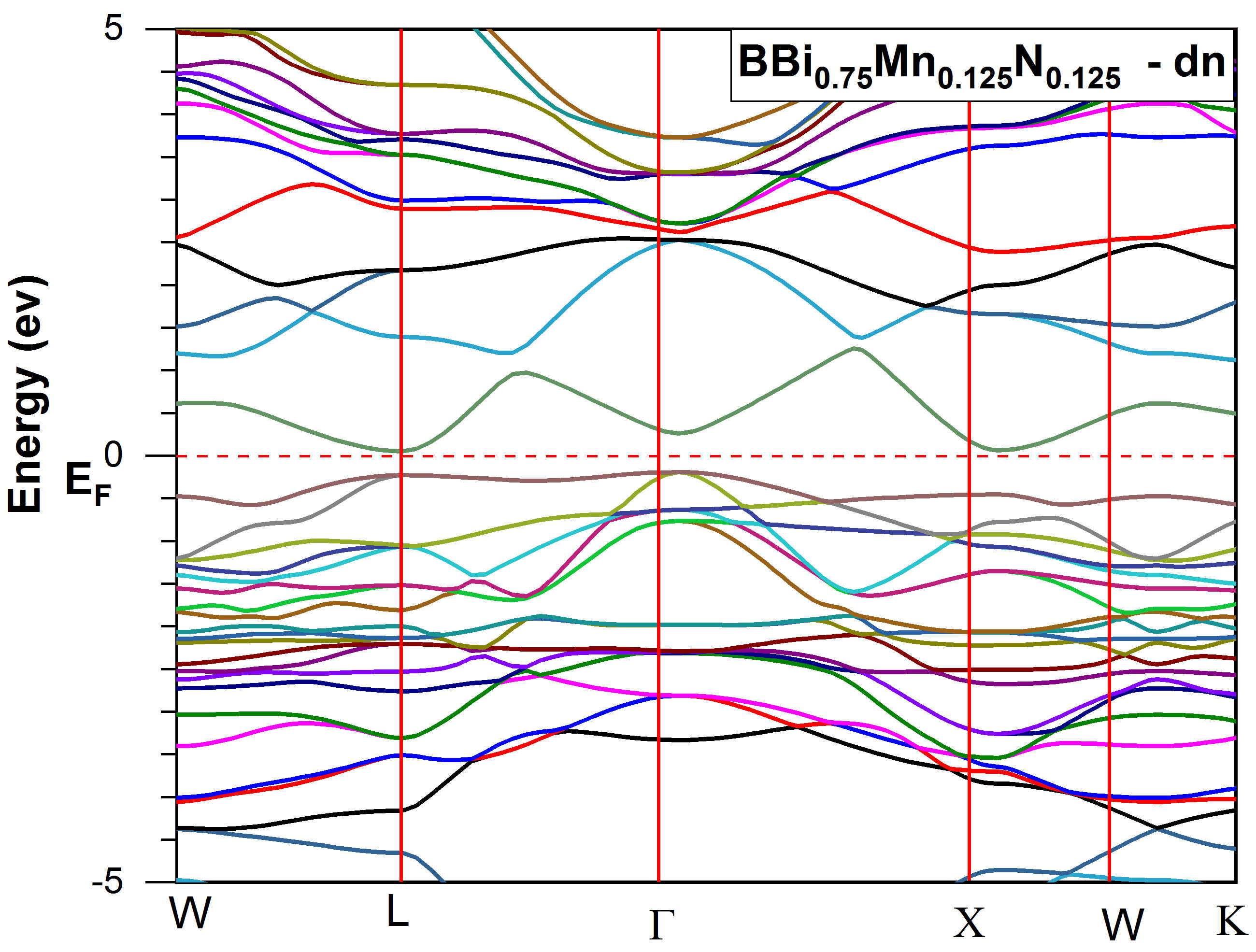
FIGURE 2 Spin-polarized band structure obtained with TB-mBJ for BBi0.75 Mn0.125 N0.125 : for majority spin (up). The Fermi level is set to zero (horizontal dotted red line).
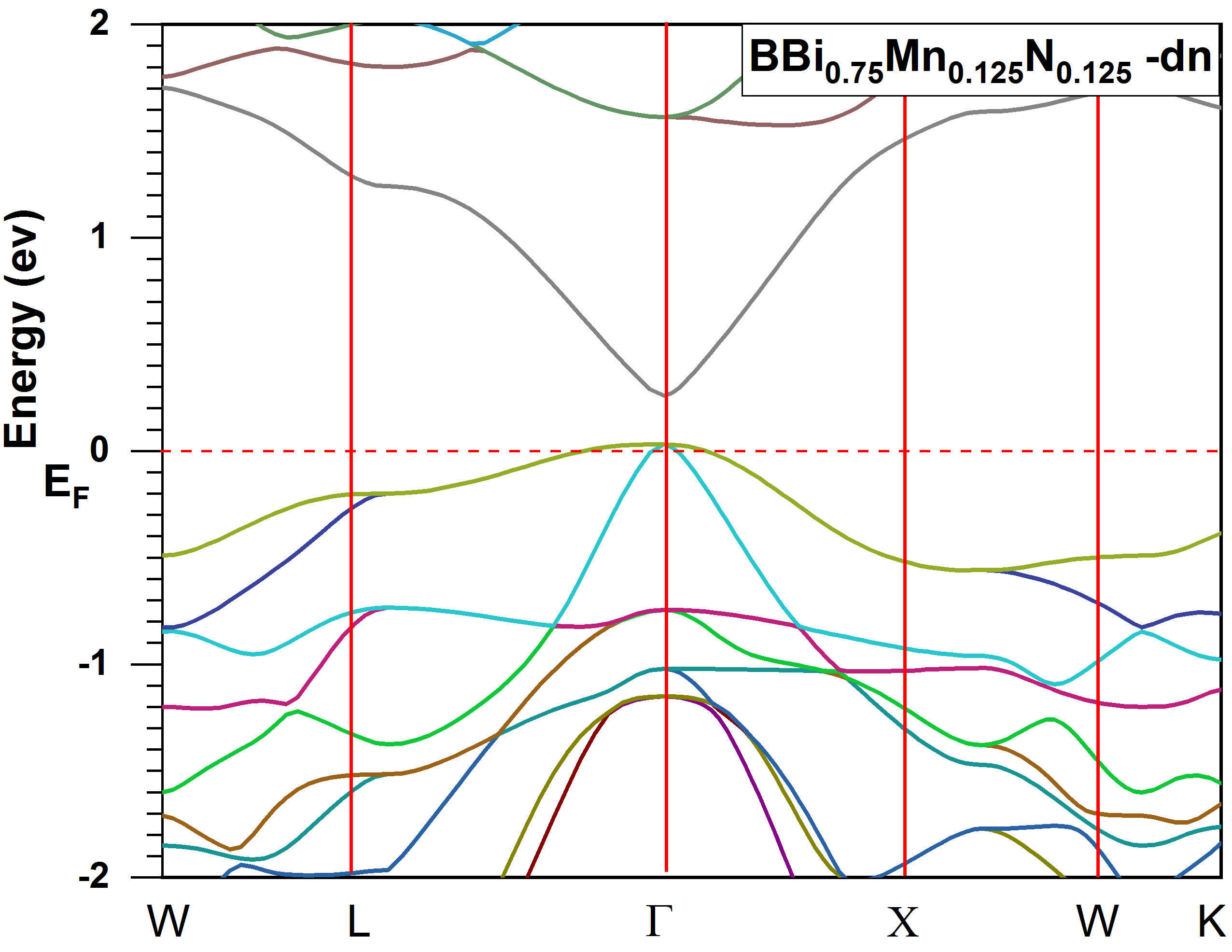
FIGURE 3 Spin-polarized band structure obtained with TB-mBJ for BBi0.75Mn0.125N0.125: for minority spin (dn). The Fermi level is set to zero (horizontal dotted red line).
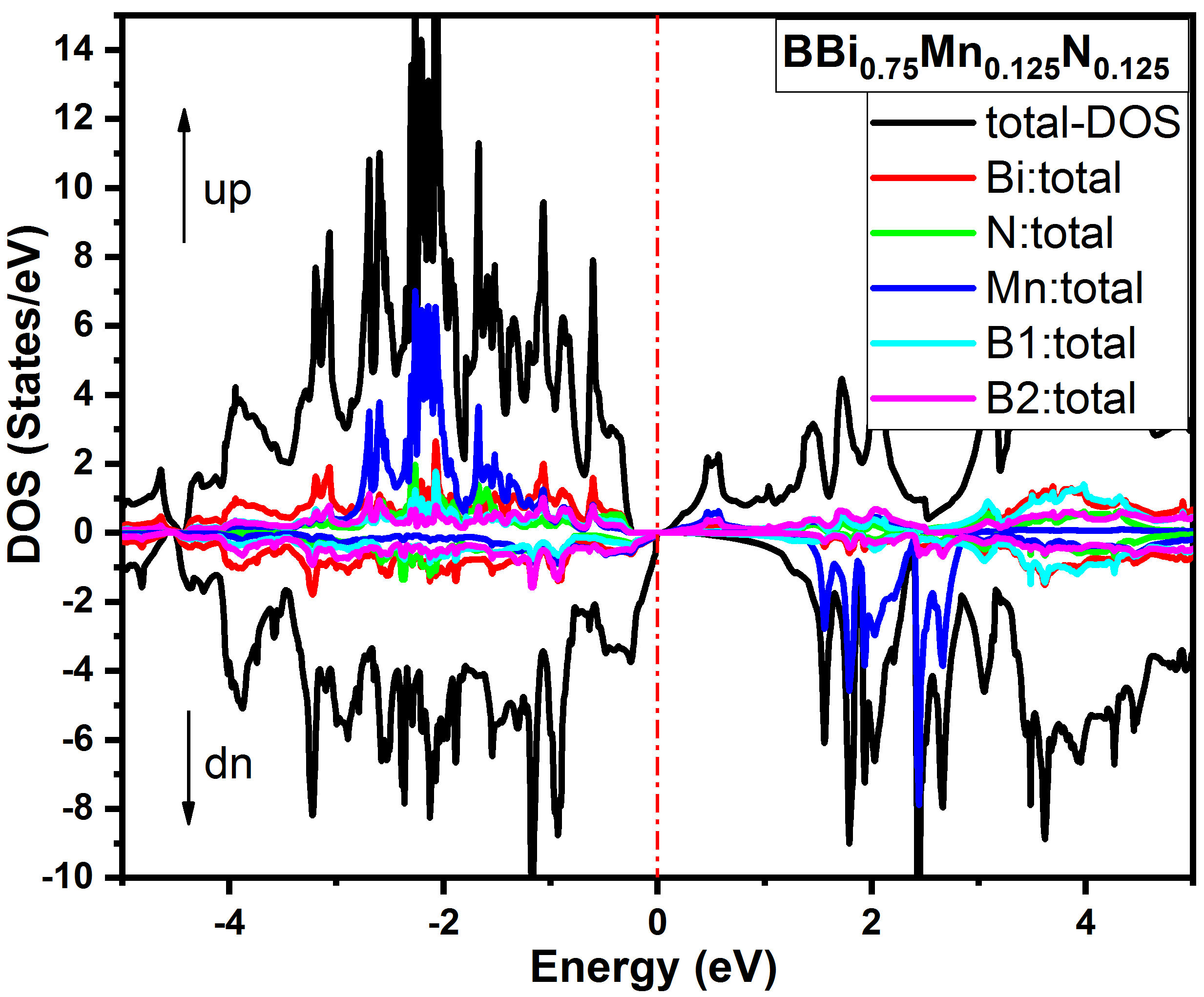
FIGURE 4 Spin-polarized total and partial densities of states of BBi0:75Mn0:125N0:125. The Fermi level is set to zero (vertical dotted red line).
4. Conclusion
In this paper, the GGA-PBEsol coupled with TB-mBJ study to investigate the elastic, electronic and magnetic properties within the framework of density functional theory based on FP-LAPW method. The results show that BBi 0.75 Mn 0.125 N 0.125 structure is stable in the ferromagnetic phase and mechanically. The compound has half-metallic ferromagnetic and can be used in spintronics applications.
From our knowledge, there are no previous theoretical or experimental studies on the BBi0:75Mn0:125N0:125 material, thus we hope that our results serve as a reference for future theoretical and experimental research.











 nueva página del texto (beta)
nueva página del texto (beta)