nueva página del texto (beta)
Inglés (pdf)
Artículo en XML
Referencias del artículo
Traducción automática
Enviar artículo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
1. Introduction
The concept of highly dispersive optical solitons emerged during 2019 as an extension and/or generalization to cubic-quartic solitons. Analytical results are abundant and stem from this concept, and these have been recovered after implementing of algorithms. These include extended trial function method, F-expansion scheme, Jacobi’s elliptic function expansion, exp-expansion and others [1-5]. The conservation laws for such solitons have also been reported [3]. Therefore, it is now time to turn the page and explore this topic from a numerical perspective. This paper, therefore. addressed highly dispersive optical solitons, having Kerr law of refractive index, by the aid of the Laplace-Adomian decomposition scheme. The focus on this paper will be on bright optical solitons. The scheme is first explicitly elaborated and subsequently implemented into the model equation successfully. The details are sketched in the rest of the paper.
2. Governing equation
The dimensionless form of NLSE with Kerr law nonlinearity in presence of dispersion terms of all orders is [6]:
where q = q(x,t) is a complex-valued function of x (space) and t (time) and i = √-1 The first term represents linear temporal evolution. The next six terms are dispersion terms that make the solitons highly dispersive. These are given by the coefficients of a K for 1 ≤ k ≤ 6, which are intermodal dispersion (IMD), group velocity dispersion (GVD), third-order dispersion (3OD), fourth-order dispersion (4OD), fifth-order dispersion (5OD) and sixth-order dispersion (6OD) respectively. Finally, b indicates the coefficient of self-phase modulation based on cubic or Kerr nonlinearity.
2.1. Bright solitons
The bright 1-soliton solution to (1) was recently found by the authors in [6,7] using the semi-variational principle and is given by
In Eq. (2), v is the soliton velocity, ω is the angular velocity, κ is the soliton frequency, and θ 0 is the phase center.
In [7], the amplitude A of the 1-soliton was calculated as:
where:
Besides, the inverse width B of the 1-soliton is a real root of the equation:
The velocity v is given by
Finally, there are the following two relationships between the soliton frequency κ and some of the coefficients of Eq. (1), these are given by
3. Method applied
In this section, we will describe the basic theory and algorithm of the Laplace-Adomian decomposition method (LADM), used to solve nonlinear partial differential equations, and that was first proposed in [9,10].
Let us look for soliton solutions of Eq. (1) in the form q(x, t) = u(x, t) + iv(x, t). Then we can decompose the Eq. (1) in its real and imaginary parts, respectively as
To give analytical approximate solutions for Eq. (1) using LADM, we first rewrite the Eqs. (9) and (10) in the following operator form
with initial conditions u(x, 0) = ℜ(q(x, 0)) and v(x, 0) = ℑm(q(x, 0)).
In the equations system (11)-(12), the operator D t denotes derivative with respect to t, whereas that D j x is the j-th order linear differential operator δ j /δ j , and N κ represents nonlinear differential operators for k = 1, 2.
The method consists of first applying the Laplace transform ℒ to both sides of equations in system (11)-(12) and then, by using initial conditions, we have
Thus, by applying the inverse Laplace transform ℒ-1, we obtain
According to the standard Adomian decomposition method, the solutions u and v can be expressed in an infinite series as follows
Also, the nonlinear terms can be written as
and
where A n and B n are the Adomian?s polynomials [11,12], which are defined by
On making the substitution of Eqs. (17) and (18) into Eqs. (15) and (16), we can arrive at
Now, according to LADM, The following recursive schemes can be constructed
Being N1(u, v) = vu2 + v3 and N2(u, v) = uv2 + u3, using the formulas (20) and (21) some terms of Adomian’s polynomials An and Bn are given by
and
Finally, in conjunction with Eq. (24) and Eq. (25), all components of u(x, t) in Eq. (17) will be easily determined; therefore, the complete solution u(x, t) in Eq. (17) can be formally established. LADM provides a reliable technique that requires less work if compared with traditional techniques.
4. Numerical simulations
To illustrate the ability, reliability, and accuracy of the proposed method to find solutions of Eq. (1) in the case of bright solitons, some examples are provided. The results reveal that the method is very effective and simple. We now consider the initial condition at t = 0 from Eq. (2)
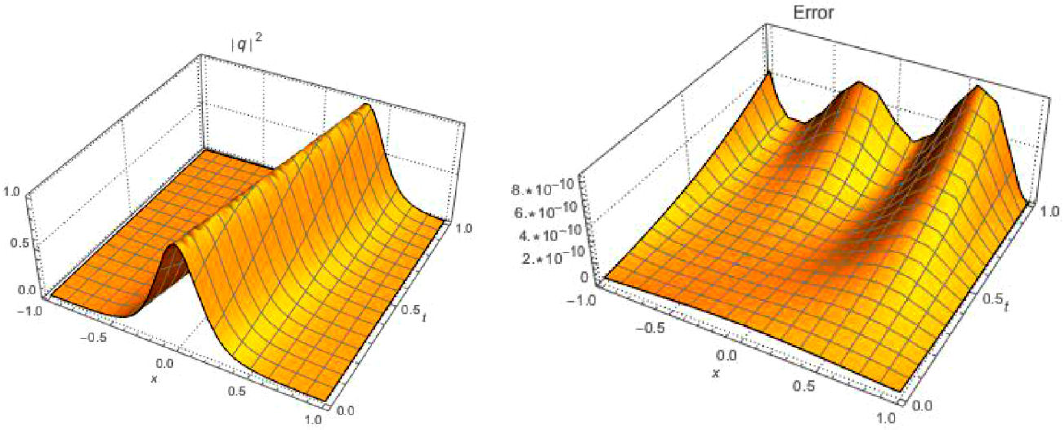
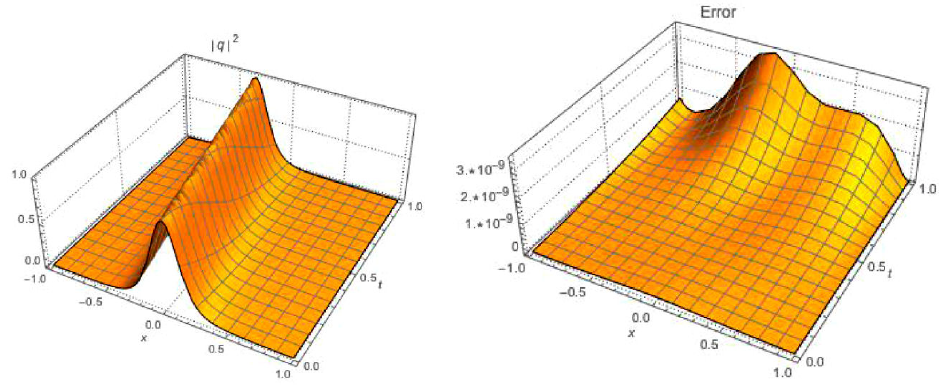
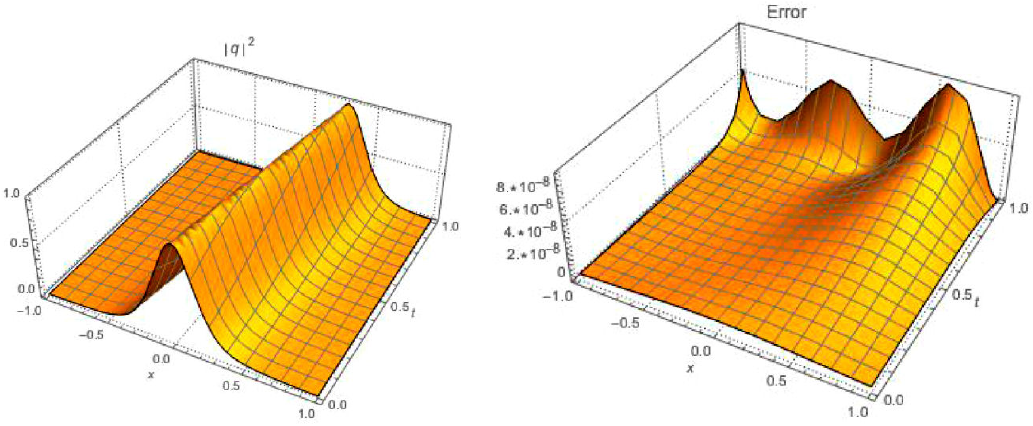
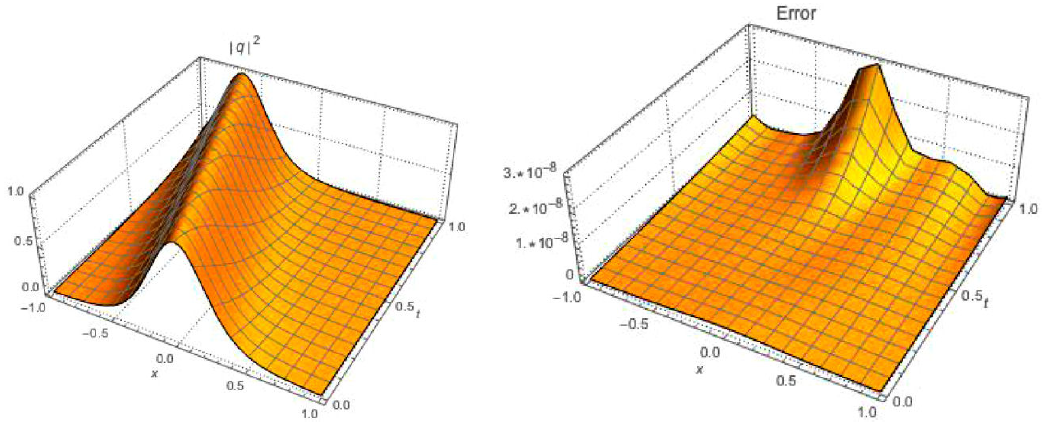
We now perform the simulation of the four cases listed in Table I, and the results and the respective absolute errors are shown in Figs. 1, 2, 3, and 4.
Table I Coefficients of Eq. (1) for bright solitons.
| Cases | a1 | a2 | a3 | a4 | a5 | a6 | b | κ | ω | θ0 | ν | N | |Max Error| |
| 1 | 1.2 | 0.01 | 0.024 | 0.50 | 4.20 | 0.33 | −1.20 | 0.01 | 0.3 | 1.2 | 1.19 | 15 | 8.0 × 10−10 |
| 2 | 1.5 | 0.07 | 0.058 | 0.25 | 3.20 | 0.16 | −1.10 | 0.03 | 0.1 | 1.4 | 1.49 | 15 | 3.0 × 10−9 |
| 3 | 1.0 | 0.09 | 0.013 | 0.12 | 1.00 | 0.08 | −1.00 | −0.02 | 0.7 | 1.6 | 1.00 | 12 | 8.0 × 10−8 |
| 4 | 1.6 | 0.04 | −0.030 | 0.80 | 1.20 | 0.10 | −1.30 | −0.01 | 0.3 | 1.3 | 1.60 | 12 | 3.0 × 10−8 |
5. Conclusions
This paper addressed highly dispersive optical solitons, with Kerr law nonlinearity, by the aid of the Laplace-Adomian decomposition scheme. The focus was on bright solitons. The numerical results supplemented the analytical results, there were reported earlier, and the agreement is to a T. The error analysis was also profoundly impressive, as well. This shows extreme promise of the numerical algorithm that has been implemented in this paper. Thus, the results of this paper will be extended to additional laws of the nonlinear refractive index. These are cubic-quartic law, polynomial law, nonlocal nonlinearity, and others. Additionally, the results will be extended to birefringent fibers. The results of such research activities are on the horizon and are soon going to be made visible.
