1.Introduction

During the past decade, a variety of nuclear phenomena like magnetic rotation ¹, chiral twin bands ², shape coexistence ^3,4, superheavy elements (5) and superdeformation ⁶ have been observed, which originate from single-particle and collective motion as well as their interplay. Traditionally, Strutinsky’s shell correction method ⁷ has been one of the central approaches for calculation of potential energy surfaces ^8,9,2, which is a key to understand these phenomena. This method, also known as the macroscopic plus microscopic approach, obtains the fluctuating part of the level density (the shell correction term) arising from the quantal shell correction energy. Parallel to Strutinsk’s method, semiclassical methods have been developed ^10-12, which can explain successfully the features of both ordered and chaotic quantum systems. Recently, the mixing of deuteron states (³ S ₁ and ³ D ₁ ) with tensor interaction has been semiclassically analyzed ¹³.

One such semiclassical technique, known as periodic orbit theory (POT), was initiated nearly four decades ago by Gutzwiller ¹⁰, it has emerged as one of the most powerful methods of understanding the quantum spectra. Semiclassical trace formula, the as developed by Gutzwiller (14) for the fluctuating part of level density of a quantum system is given by

The left-hand side of Eq. (1) is a quantum mechanical quantity, whereas the right-hand side contains only the classical quantities. Here, T _PPO represents the time period of the primitive periodic orbit, and M~PO is the monodromy stability matrix. The oscillations are controlled by action S _PO of each periodic orbit and σ _PO is a Maslov index. This trace formula is, however, applicable if all the periodic orbits are isolated.

Subsequently, several extensions of Gutzwiller’s semiclassical trace formula were made to include regular and mixed dynamics for explaining quantum shell effects in many physical systems ^15-18. One such generalization was reported by Strutinsky et al. ¹⁹ to systems with continuous symmetries by explicitly taking into account the degeneracy of the classical orbits. This method was successfully applied to phenomenological potentials used in nuclear physics ¹⁹, yielding a semiclassical interpretation of ground-state deformation as a function of particle number. One of us ²⁰ has also obtained an eigenvalue spectrum for a particle enclosed in an infinitely high spheroidal cavity by using the formalism of Strutinsky et al. On comparing this semiclassical eigenvalue spectrum with corresponding quantum mechanical values ²¹, we have established the importance and significant contribution of planar (both in the axis of symmetry plane and the equatorial plane) and 3-dimensional orbits for the normal deformed and the superdeformed regions. Further, this semiclassical method has been extended ²² to explain elegantly the mass asymmetry in nuclear fission ²³.

Amann and Brack ²⁴ have developed trace formula for a nuclear system in a 3-dimensional harmonic oscillator mean-field with a spin-orbit interaction of Thomas type. In the strong coupling limit, singularities occur in phase space where the spin-orbit interaction locally becomes zero. These singularities impose severe restrictions on the applicability of the trace formula. However, they have pointed out that the leading orbits with shortest periods are free from singularities and lead to excellent results for the coarse-grained level density, as long as bifurcations of these orbits are avoided.

It is worthwhile to mention here that Littlejohn and Flynn²⁵ developed a semiclassical theory of systems with multi-component wavefunctions and applied ²⁶ it to the WKB quantization of integrable spherical systems with the standard spin-orbit interactions. Frisk and Guhr ²⁷ have studied the deformed systems with spin-orbit interaction by approximating the Schrodinger equation semiclassically. Here, the information about the periodic orbits is extracted from the Fourier transform of the quantum mechanical spectra.

The present work aims to obtain the complete spectrum for a particle moving in an isotropic three-dimensional harmonic oscillator mean-field with spin-orbit interaction. This work is based on the formalism developed by Strutinsky et al. ¹⁹. The semiclassical interpretation for a nucleon in an isotropic oscillator mean-field was first given by Bohr and Mottelson ²⁸. They pointed out that only the pendulating orbits (also known as diametric orbits) are possible in this potential. These orbits are traced by a particle by executing two radial oscillations for each angular motion (i.e. (ω _r /ω _θ = 1/2). Such a trajectory coincides with l= 0 axis. We will show that our periodicity condition confirms their observation, and the calculated eigenvalue spectrum is exactly in agreement with a quantum mechanical one.

Further, the effect of spin-orbit coupling in the mean-field arises only if there is a contribution of orbits with l≥ 0. Such trajectories are obtained in our trace formula by putting the constraint that the particle is reflected at r=R ₀ (R ₀ being the nuclear radius), instead of infinity. This is an ideal situation for the nuclear shell model, which states that a particle moving in harmonic oscillator mean-field is confined in a spherical cavity of radius R ₀ . In this work, we have fixed the potential strength with the help of virial theorem. The complete formalism is free from singularities and does not involve any fitting parameter.

A complete trace formula for a particle moving in a three-dimensional harmonic isotropic oscillator mean-field with spin-orbit coupling is given in Sec. 2. Section 3 is devoted to results and discussion. The conclusions are summarized in Sec. 4.

2.Trace formula for isotropic harmonic oscillator mean-field with spin-orbit coupling

For the bound states of a single particle Hamiltonian H, the level density is generally defined as a sum of Dirac delta distributions,

This sum runs over all the eigen-energies E _i (including degeneracies). It can split into a smooth and an oscillating part:

The oscillating component of the single particle level density δg(E), in cylindrical coordinates (ρ,ϕ,z) is given by

The factor f _β,m equals to 1 for the diametric orbits and 2 for other orbits like triangles, squares, etc. The time-period for the path from the initial point FORMULA to the final point FORMULA for energy E is defined as

The quantity J in Eq. (4) is the Jacobian of transformation between two sets of classical quantities (p _ρ ,P _z ,t _β,m ) and (ρ′,z′,E), which are related by the classical equations of motion. Here, β denotes the type of orbits and m is the number of reoetitions of a given type of orbit.

The periodic orbit sum in Eq. (4) does not converge in most cases. Since the maximum contribution to the gross shell structure comes from the shortest periodic orbits. It has now become customary to carry out a smooth truncation of the contributions of the longer periodic orbits by folding the level density with a Gaussian function ¹² of width γ,

The averaging width γ is chosen to be larger than the mean spacing between the energy levels within a shell, but much smaller than the distance between the gross shells. This averaging ensures that all longer paths are strongly damped and only the shortest periodic orbits contribute to the oscillating part of the level density. Also, the effect of degeneracies is included in Eq. (4) by using the prescription outlined in Ref. ¹⁹.

We have approximated the nuclear mean-field by an isotropic harmonic oscillator. The Hamiltonian for a single particle of mass M is expressed in terms of spherical polar coordinates (r,θ,ϕ) and the conjugate momenta (p _r ,p _θ ,p _ϕ ) as

Equation (7) leads to a Hamilton-Jacobi equation, which can be solved by using the separation of variable technique. Therefore, the classical dynamics of a particle is determined by the following three partial actions:

Here, ε and l _z are the separation constants and are obtained from the following periodicity conditions.

The integration in the r-coordinate of Eq. (9) is obtained analytically under two limiting approximations: (i) the upper limit lies at infinity and (ii) it lies at R ₀ . Both these cases are discussed in the following subsections.

3.Results and discussion

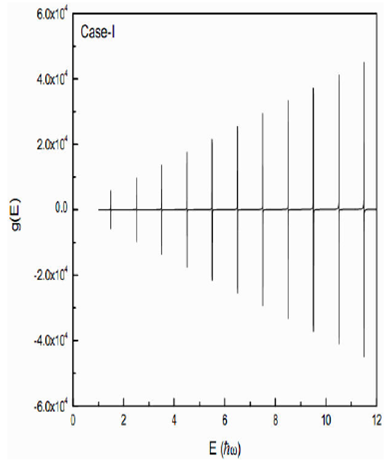
Firstly, we discuss the semiclassical eigenvalue spectrum of isotropic harmonic oscillator without l→⋅s→ coupling. Further, the numerical results of case I are presented first. In this case, we have varied n _θ from 1 to 500. The periodicity conditions (Eqs. (11) and (12)) fix n _r (=2n _θ ) and n _ϕ (=n _θ ), respectively. Since only one type of orbits, known as diametric orbits are involved, the repetition parameter m is kept equal to 1. The averaging width γ is chosen as 0.002 for proper convergence of the sum in Eq. (4). Here, the energy is measured in units of ℏω. The results of g(E) vs. E are shown in Fig. 1. It is interesting enough to note that the peak positions coincide exactly with those of the quantum levels E _N = (N+(3/2))ℏω (with N= 0, 1, 2, 3 etc.) and peak heights resemble nearly with the quantum mechanical degeneracies (1/2)(N+1)(N+2). Here, we would like to mention that the difference between the semiclassical eigenvalues and quantum mechanical ones is 2×10⁻³. An analytically exact result was already obtained in Ref. ¹⁵ by modifying the Gutzwiller’s trace formula for stable orbits. It is worthwhile to mention here that the frequency ratios in our approach are fixed by the periodicity conditions. Also, the trajectories fixed by the periodicity conditions in our approach fully support the observation made by Bohr and Mottelson ²⁸ that only the pendulating orbits are possible in an isotropic harmonic oscillator potential.

The number of particles are obtained by using the relation:

Here, E _F refers to energy corresponding to the peak position in Fig. 1 and g(E) is the total level density. The calculated results of N vs. E are shown in Fig. 2. The quantum mechanical results are also shown in this figure. A comparison of semiclassical results with those of quantum mechanical ones shows a remarkable similarity in the variation of N vs. E. However, the semiclassical values are an order of magnitude higher than the quantum mechanical values. This order of magnitude can be reduced by incorporating the Pauli-principle in the trace formula ³¹; it is not included here. The diametric trajectories correspond to l= 0 contribution and hence do not reproduce splitting by including the l→⋅s→ coupling (as discussed above in Sec. 2.3).

Figure 1 Total level density g(E) vs. E in units of ħω for Case I of isotropic oscillator. 

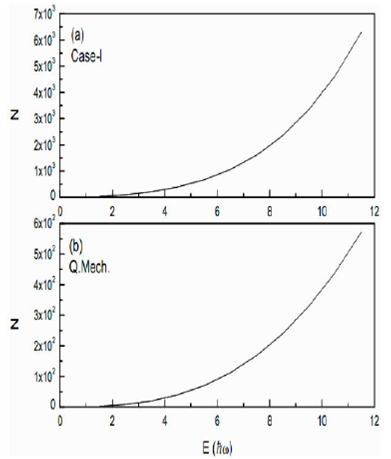
Figure 2 (a) Particle number N vs. E in units of ħω for Case I of isotropic oscillator. (b) Plot of Quantum results. 

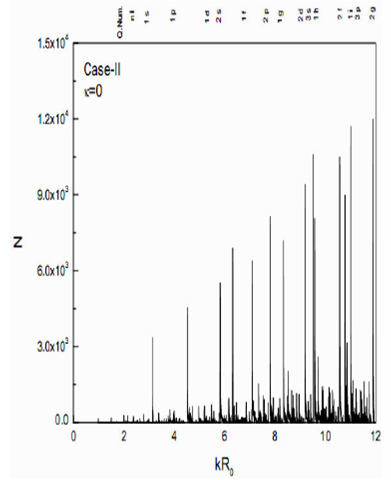
To obtain the splitting due to l→⋅s→ coupling, we have switched over to case II. In this case, we have varied both n _θ from 1 to 500 and n _r from 2n _θ to 500, whereas n _ϕ is fixed equal to n _θ by using the periodicity condition Eq. (12). These varied integers are used in Eq. (24) to obtain trajectories with l≥ 0. Further, we have solved simultaneously the transcendental Eqs. (24) and (25) to ascertain the shapes of trajectories possible in the harmonic oscillator mean-field. Here, γ is again fixed equal to 0.002, and the upper limit of the repeated orbits, m _max is obtained by Eq. (29). We have already pointed out that this scenario resembles a spherical cavity problem. Therefore, we have calculated the energies in units of ℏ²/2MR ₀ ². The results of g(E) vs kR ₀ (where k=2ME/ℏ are shown in Fig. 3. It is obvious that the peak positions show a similar eigenvalue spectrum as observed in a spherical cavity ³⁰, and are fairly close to the zeroes of Bessel functions (which are the quantum mechanical results of a single particle confined in spherical potential well). Here, we would like to point out that for an exact comparison with the quantum mechanical results, one has to solve the quantum mechanical eigenvalue equation for such a truncated mean field at R ₀ .

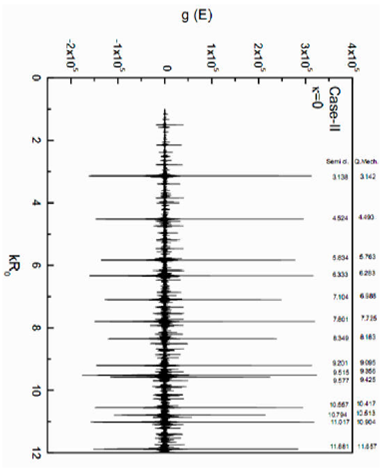
Figure 3 Total level density g(E) vs. kR0 for Case II of isotropic oscillator with κ = 0. The quantum results are also given for comparison. 

The particle numbers are calculated by using Eq. (41) and are shown in Fig. 4 as a function of kR ₀ . Here, F _F in terms of kR ₀ is varied continuously from 1 to 12. Again the calculated N values are quite high as compared to quantum results, which can be reduced by including Pauli-principle in the trace formula. If we compare this plot with the quantum numbers which are also identified at the top of this plot, the following interesting features emerge:

Figure 4 Particle number N vs. kR0 for Case II of isotropic oscillator with κ = 0. 

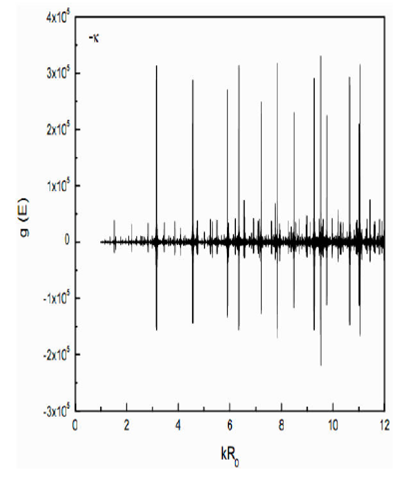
Another advantage of this study is to show the splitting of the eigenvalue spectrum by including the l→⋅s→ coupling in the nuclear mean-field. The inclusion of l→⋅s→ coupling involves positive as well as negative signs with κ in the quantities used for calculation of the fluctuating part of the level density. Figures 5 and 6 show the results of total level density, g(E), as a function of positive and negative signs with kR ₀ in Sec. 2.3), respectively. These results are also tabulated in Table I together with the quantum mechanical results of the spherical cavity without l→⋅s→ coupling. The semiclassical results without l→⋅s→ coupling are also given in this table. On comparing the results of positive and negative contributions, it is observed that the eigenvalues corresponding to negative sign are higher as compared to those of positive sign. Further, a comparison of these eigenvalues with the results of the harmonic oscillator (Case II) having zero l→⋅s→ coupling shows that each level is split into two. The splitting width of each level is consistent with the quantum mechanical results as discussed below.

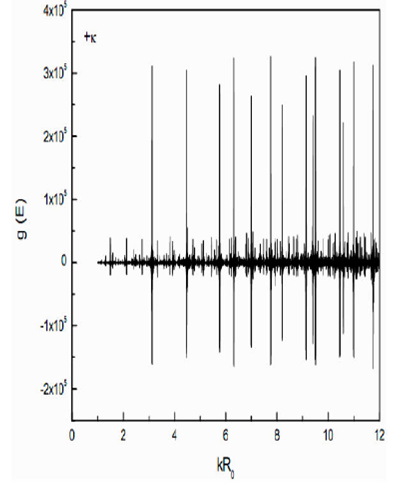
Figure 5.Total level density g(E) vs. kR0 for combination of Case II and positive sign with k in l→⋅s→ coupling. 

Figure 6 Total level density g(E) vs. kR0 for Case II and negative sign with κ in l→⋅s→ coupling. 

In nuclear system with l→⋅s→ coupling, we get two eigenvalues for each angular momentum l, which are equal to −κ×l for j=l+(1/2) and κ×(l+1) for j=l−(1/2). A similar splitting is observed in our semiclassical approach. The quantum spectrum does not split the eigenvalue corresponding to l= 0 level, whereas in semiclassical calculations each level is splitted into two. It is quite interesting to note in Table I that, corresponding to each quantum mechanical s-state, the semiclassical splitting is extremely small ∼0.027 as compared to other states. Also, the splitting width ΔE is nearly proportional to (2l+1) the s-state splitting for each l (where l refers to the quantum number in Table I). It is a remarkable observation and fully supports the nuclear shell model spectrum. Further, it is noticed that the simultaneous solution of Eqs. (39) and (40) with the minus sign gives the diametric orbits, whereas no such trajectories are seen with the positive sign. These diametric orbits refer to l= 0 as pointed out by Bohr and Mottelson ²⁸. Therefore, its absence in one choice of sign (+), leads to a small splitting in the s-state.

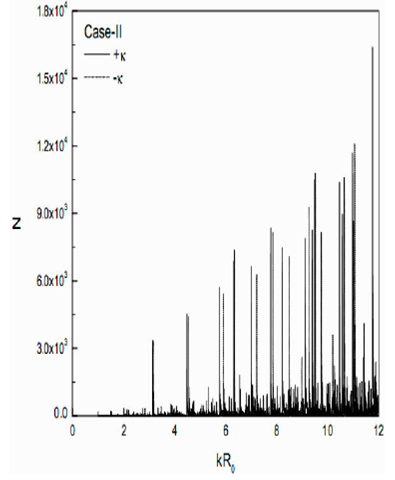
Finally, the total level density g(E) vs kR ₀ , including both positive and negative signs with κ, is shown in Fig. 7, respectively, by solid and dotted curves. The resultant eigenvalue spectrum clearly shows the splitting.

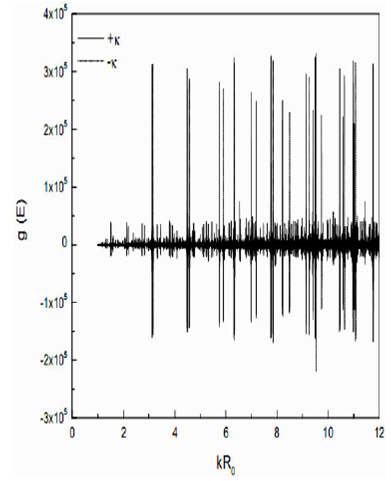
Figure 7 Total level density g(E) vs. kR0 for Case II including both positive and negative signs with κ in l→⋅s→ coupling. 

The plot of the number of particles, vs kR ₀ with both positive and negative signs of κ are shown by solid and dotted curves, respectively, in Fig. 8. It is evident from this plot that the dotted curve refers to the quantum mechanical case of j=l−(1/2), whereas the solid curves refer to j=l+(1/2). The number of particles shown by the dotted curve is less than those of a solid curve in a particular shell, which again supports the quantum mechanical observation. In order to get a reasonable separation in kR ₀ at the magic numbers 28, 50, etc., we have to adjust the splitting parameter λ, which we have chosen equal to 0.2. Thus a complete semiclassical picture of the nuclear shell model is obtained, which will help predic the next magic numbers.

Figure 8 Particle number N vs. kR0 for Case II including both positive and negative signs with κ in l→⋅s→ coupling. 

4.Conclusion

A trace formula for the level density of an isotropic harmonic oscillator with l→⋅s→ coupling is presented. Our formalism reproduces the eigenvalue spectrum of pure quantum oscillator exactly. The contribution of angular momentum is generated by terminating the upper limit at the nuclear radius R ₀ , which fully reproduces the resultant nuclear spectrum with l→⋅s→ coupling. We have established the role of significant quantum numbers ‘n’ and ‘l’ in this semiclassical method. The overall eigenvalue spectrum compares reasonably well with that of the nuclear shell model (with magic numbers) without any fitting parameter.