PACS: 31.15.Pf; 31.10.+z; 32.60.+i; 97.10.Ld
1. Introduction
The elucidation of the origin of the spectra coming from magnetic white dwarfs and neutron stars is only possible if we understand the behavior of simple atoms and molecules in the presence of strong magnetic fields. Chemistry of molecules in strong magnetic fields is quite different from traditional chemistry. For example, in strong magnetic fields, the presence of exotic species of atoms and molecules is possible (the case of one-two electron systems made out of protons and/or alpha particles is reviewed in 1 and 2 and references therein). Exotic molecules in strong magnetic fields were predicted by Ruderman 3,4 when he suggested that in strong magnetic fields linear chains of Hydrogen are formed along the magnetic field orientation. These predictions were motivated by the presumable existence of strong magnetic fields B ∼ 1012 G in neutron stars. Currently, such magnetic fields in neutron stars are confirmed by observations, and there is evidence 5 that even stronger magnetic fields can appear in magnetars (B ∼ 1014−15 G). Since then, the study of molecules and atoms in strong magnetic fields has gained relevance. In particular, from the observation by the Hubble Space Telescope of Helium atmospheres in magnetic white dwarfs 6 and more recently, from observations by Chandra X-Ray Observatory in 2002 when they detected a considerable amount of data of thermal emission showing clear signals of absorption features from the surface layer of the isolated neutron star 1E1207.4-5209 7, which is characterized by an enormous magnetic field B ≳ 1012 G. This conclusion was supported in 2003 by observations of XMMNewton X-ray Observatory 8 (see also 9). The origin of these absorption lines in spectra is not fully understood yet. Simple spectral models demonstrate that the atmosphere of the 1E1207 object cannot be Hydrogen or ionized Helium in ultra-strong magnetic fields, but leading to the extreme conclusion that the presence of oxygen or neon can possibly explain the absorption features (see for example 10). Other possibilities led to the proposal of models based on the existence of simple exotic compounds like
The simplest molecule
In the presence of a uniform magnetic field the ground state remains stable for any orientation of the magnetic field, and the well becomes deeper as the magnetic field increases. The parallel configuration realizes the optimal configuration of minimal total energy. For larger magnetic fields, the domain of inclinations where the
The case of the 1u state in a magnetic field is by far, much less studied. The majority of studies were performed for the parallel configuration. Previous studies of this state in an arbitrarily oriented magnetic field only found stability when the molecular axis is oriented along the magnetic field lines and for relatively small strengths. In some cases, the accuracy of calculations has not allowed to make a definitive conclusion about the stability with respect dissociation and nuclear motion effects (see 1).
The present study is focused to the 1u state of
2. Hamitonian
The Hamiltonian which describes a system of two infinitely massive protons and one electron (ppe) (or
where
A 2-parameter vector potential corresponding to the magnetic field (2) is given by
where λ1 and λ2 are two arbitrary parameters. Gauge (3) satisfies the Coulomb gauge (∇ · 𝒜(r) = 0). The symmetric gauge (𝒜 = (1/2)B × r) corresponds to the case λ1 = −(1/2)cosθ and λ2 = −(1/2)sinθ. For a magnetic field oriented along the z-axis (θ = 0°), the Landau gauge corresponds to λ1 = −1 and λ2 = 0. Gauge (3) includes a) the linear gauge 𝒜 = ((1 + λ1)y, λ1x, 0) if λ2 = 0 for a magnetic field oriented parallel to the z-axis, and b) the linear gauge 𝒜 = (0, λ2z,(1+λ2)y) if λ1 = 0 for a magnetic field oriented parallel to the x-axis. The parameters λ1 and λ2 will be treated a priori as independent variational parameters in the present study.
Using the gauge (3) defined by 2 parameters, the Hamiltonian takes the form
In the parallel configuration, the problem is characterized by the quantum numbers corresponding to: (i) spatial parity p and (ii) the angular momentum projection m on the magnetic field direction (z-direction). In cases of arbitrary inclination of the magnetic field, axial symmetry around z-axis does not exist, therefore only spatial parity p characterizes the system. The notation we use for the different states is based on the following convention: the first number corresponds to the number of excitation - “principal quantum number”, e.g. the number 1 is assigned to the ground state, the number 2 to the first excited state, and then a subscript g/u (gerade/ungerade) corresponding to positive/negative eigenvalues of the parity operator.
3. Method
Since we used an approximate method for solving the Schrodinger equation with the Hamiltonian
(1), our approx-¨ imate energies can well be gauge-dependent (only the exact ones
are gauge-independent). The present study is based on the variational method with
the form of the vector potential chosen in a certain optimal way. The choice of
trial functions is made according to the following recipe: As a first step, we
construct an adequate variational real trial function
Ψ014,15,16,17, for which the associated potential
V0 ≡ (∆Ψ0
/Ψ0) reproduces the original potential near Coulomb
singularities and the harmonic oscillator behavior (transverse to the magnetic field
direction) at large distances. The trial function should support the symmetries of
the original problem. We then performed a minimization of the energy functional by
treating the free parameters of the trial function and the parameters
λ1 and λ2 defining the
vector potential on the same footing. Such an approach enables us to find the
optimal form of the Hamiltonian as a function of
λ1 and λ2. It is worth
to emphasize one important assumption in the present study. Namely, that for a fixed
value of B and a given inclination, we can find a gauge for which
the eigenfunction is realii. This gauge optimization is nothing
but a mechanism to justify the use of real trial functions. Therefore one can
discard any imaginary term in the Hamiltonian. This prescription was used in 1 and led to adequate trial functions
to study the two lowest states of
A key point in the present study is based on the observation that in the Landau problem (one electron in a constant magnetic field) with the magnetic field given by (2) and the corresponding vector potential (3), the exact (real) eigenfunction for the ground state is given by
where
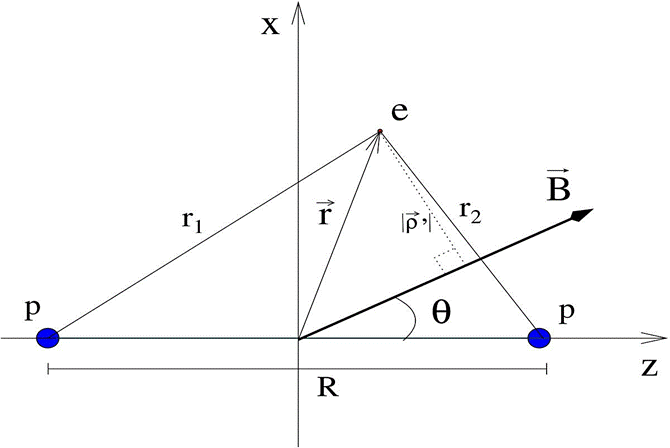
Figure 1 Geometrical setting for the
Motivated by the exact solution (5) for an electron in the presence of a constant magnetic field given by (2) we propose a trial function of the form
which is a (symmetric (gerade)/antisymmetric (ungerade)) function with respect to the interchange of the nuclei, of the Guillemin-Zener type multiplied by the Landau factor in the form (5). In (6) α3, α4, β3x, β3y, β3z and βc are variational parameters. So, this function is characterized by 6 variational parameters. The function (6) is a modification of the Guillemin-Zenner type function used in 1. Due to the symmetrization the trial function (9) can be separated in two terms ψGZ−a,b. Following a criterion of physical adequacy described in 14, the associated potential (V = ∆Ψ/Ψ) corresponding to the first term ψGZ−a of the trial function (6) is
The dominant terms in the associated potential VGZ−a reproduce the terms of the original potential in (4), for the symmetric gauge, if α3 = α4 = 1, β3x = cos2θ, β3y = 1, β3z = sin2θ, βc = 2cosθ sinθ. The associated potential contains additional terms which are sub-dominant near Coulomb singularities and at large distances. It is important to mention that if the parameters βc = β3 = 0, then the associated potential reproduces the potential and, correspondingly, the trial function used in 1. This situation occurs in the configurations of maximal symmetry 0° and 90°.
The Guillemin Zener type function (6) reduces to the particular cases of Heitler-London type, and Hund-Mulliken type functions, when α3 = α4 and α3 = 0, respectively.
3.1. Trial function
In order to describe the 1u state we consider in the present study a linear combination of three functions: two functions of the Guillemin-Zener type, each with its own variational parameters, and one Ansatz of the Hund-Mulliken type:
where α2, β2x, β2y, β2xz, βc are variational parameters. The Hund-Mulliken type function describes adequately the physical situation of large internuclear distances. On the other hand, the Guillemin-Zener type function describes adequately the domain of intermediate and small internuclear distances. Thus, the complete trial function proposed in this study is the linear combination
where the coefficients A1, A2, A3 are considered as variational parameters. One of these parameters can be chosen arbitrarily as a part of the normalization of the trial function. In general, the total number of variational parameters in (9) is 20 and the total number of parameters including R and the gauge parameters λ1,2 is 23.
In the particular case of the parallel configuration, the system exhibits an azimuthal symmetry around the axis of the magnetic field. This azimuthal symmetry reduces effectively the total number of parameters, because the parameters in front of the crossed terms xz, and in front of the z2 terms in the Landau factor in (6) i.e. βc and β3z, must be zero in order to reproduce the corresponding magnetic field oriented along the z-axis. It is worth to mention that, in this parallel configuration, the trial function (9) coincides with that used in 1 with an additional second Ansatz of the GuilleminZener type.
3.2. The Hellman-Feynman theorem: Configurations of maximal symmetry
The configurations of maximal symmetry are especially relevant from a theoretical point of view. Some qualitative features of any system with an explicit dependence on a certain parameter can be predicted through the Hellman-Feynman theorem. For the particular system of
where Ψ is the variational wave function (a stationary point for the Schrodinger functional) corresponding to the eigen- value E, and H is the Hamiltonian of the system.
Considering that the trial function (9) is real, the extremals of the total energy as a function of the inclination angle θ, are found by the relation
where
Thus, using the variational results (see e.g.Table V) we verify that Eq. (11) is satisfied in the configurations of maximal symmetry
This relation should be gauge invariant. A similar analysis was done in 18 where the symmetric gauge was used leading to the same conclusion. It is also worth to notice, that in the case when the magnetic field is chosen along the zaxis and the molecular axis is inclined (as it was done in 1) there is no explicit dependence on the inclination angle in the Hamiltonian, and the Hellman-Feynman theorem cannot be applied.
4. Results
We carried out a variational study of the 1u state of the system (ppe) with infinitely heavy nuclei, interacting with a magnetic field 0 < B ≤ 10 a.u. in inclined configuration 0° ≤ θ ≤ 90° with respect to the molecular axis. In this range of magnetic fields the total energy of the 1u state presents a pronounced minimum. Our variational results indicate that there exist some critical fields and critical inclinations where the 1u becomes unstable towards dissociation
The numerical calculation was developed using subroutines D01FCF of NAG-LIB 19 for the 2(3) dimensional integrations (depending to the symmetry of the configuration) and the package MINUIT of CERN-LIB 20 to minimize the energy functional. In order to reach a higher (and stable) accuracy, the (finite) domain of integration was manually and conveniently subdivided following the profile of the integrand. Usually, the domain of integration along each coordinate was subdivided into 3 or more subregions. The variational results are presented with an estimated relative accuracy of 10−6.
4.1. Configurations of maximal symmetry
The results of our variational calculations with the trial function (9) for the 1u state of
Table I Total, ET, binding, Eb = Ee −ET, energies and equilibrium distance Req for the state 1u as a function of magnetic field B in the parallel configuration θ = 0° which becomes 1σu. This state represents the first excited state or the ground of state of negative parity. The optimal gauge is found to correspond to the symmetric gauge (λ1 = −1/2,λ2 = 0) for all magnetic fields. The ground state of energy of the Hydrogen atom 1s027 is presented in the last column for comparison. The horizontal line divides the fields where the 1u is stable/unstable.
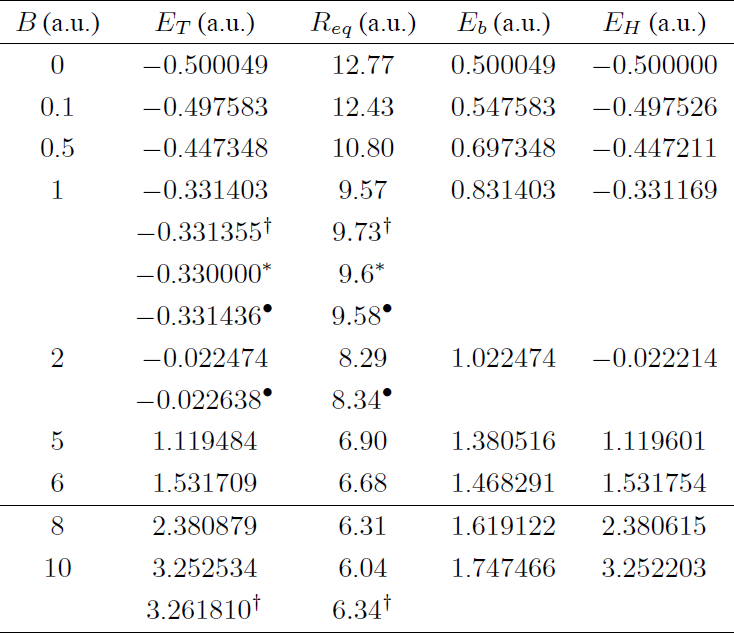
† results from 1.
∗ results from 24.
• results from 25.
Table II Total, ET, binding, Eb, energies and equilibrium distance Req for the state 1u as a function of magnetic field B in the perpendicular configuration θ = 90°. This state represents the first excited state or the ground of state of negative parity. The optimal gauge is found to correspond to ∼ Landau gauge (λ1 = 0,λ2 = −0.08) for all magnetic fields. The ground state of energy of the Hydrogen atom 1s027 is presented in the last column for comparison. The horizontal line divides the fields where the 1u is stable/unstable.
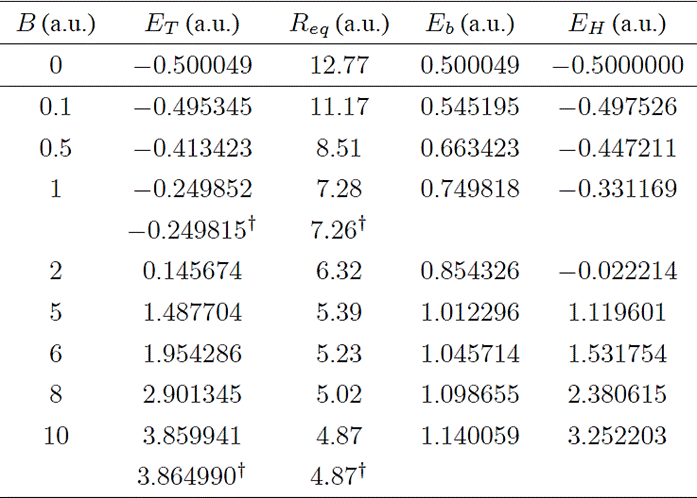
† Results from 1.
In the parallel configuration our results for the total energy of the 1u state are in excellent agreement with the best results 21,22,23,24,25. For example, for B = 1 a.u. the difference with respect to the best known results existing in the literature 25 is beyond 10−5 a.u. Qualitatively, we observed a monotonous increase in the total E T and bindiniii energy E B , accompanied by a monotonous decrease in the equilibrium internuclear distance Req as a function of magnetic field (0 ≤ B ≤ 10 a.u.) It is worth emphasizing that in this particular configuration, our results improve slightly the results from 1 with a simple addition of one Guillemin-Zener type function (the improvement was ∼ 10−5 for B = 1 a.u.). However, such a small difference may be enough to confirm or discard stability in some cases. The fact that we obtained a small improvement in the total energy, even adding one more Guillemin-Zener term to the trial function (i.e. 5 more variational parameters), can be interpreted as a manifestation of the convergence of the trial function. However, the obtained equilibrium distance Req = 9.57 a.u. at B = 1a.u. shows a better agreement with results in 24,25 (see Table I).
The 1u state in the perpendicular configuration has received less attention in the literature. The only exceptions are references 24,25,26 iv. In the perpendicular configuration, the system also exhibits an increasing behavior of the total and binding energies as a function of the magnetic field, accompanied by a monotonous decrease in the equilibrium internuclear distance (see Table II). For all the magnetic fields considered, the total energy for the 1u state in the perpendicular configuration is always larger compared with the energy in the parallel configuration. Also, for all magnetic fields studied, we observe that in perpendicular configuration the system is more compact (the internuclear equilibrium distance is smaller) in comparison to the parallel configuration (e.g. by ∼ 2.3a.u. at B = 1a.u.)
One of the main goals of the present study is to find the optimal configuration (of lowest total energy) for this state. From our variational results, we confirm the conjecture that the parallel configuration realizes the configuration of minimal total energy of the
The difference between the energies of maximal symmetry configurations increases as a function of the magnetic field (∆E = ET (90°) − ET (0°) = 0.8 a.u for B = 1 a.u.), such behavior is interpreted as the 1u state becomes more rigid towards rotations as the magnetic field increases.
4.2. Stability of 1u state: Critical Fields
One can observe from Table I and Table II that the 1u state is not stable for all the magnetic fields. First of all, it is important to emphasize that a high accuracy was required in order to analyze the stability the 1u state, since it is a weakly bound state and the potential well is very shallow. The present variational results show that the energy of the 1s ground state of Hydrogen atom and the total energy of the 1u state of
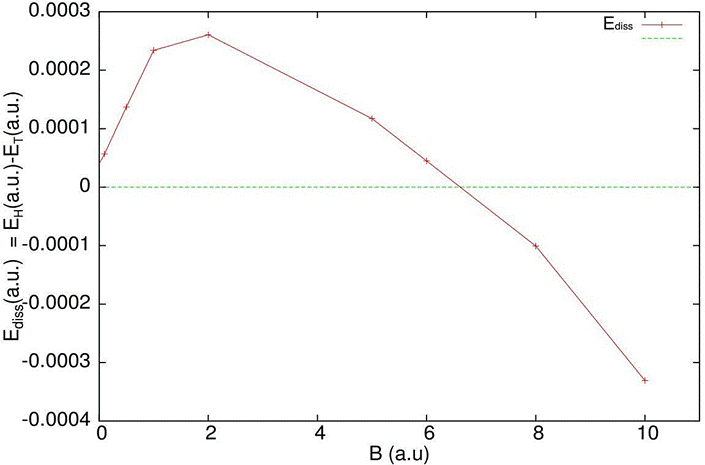
Figure 2 Dissociation energy Ediss = EH −ET of the 1u state of
Our variational results show that in the parallel configuration the 1u state is stable towards dissociation
As for the parallel configuration we can do a similar analysis for the perpendicular case. In this configuration the 1u state is only stable for magnetic fields B < 0.1 a.u. Thus, the domain of stability in the perpendicular configuration is quite smaller compared with that of the parallel configuration. The critical magnetic field is estimated at B = 2 × 10−3 a.u.
In both configurations, for all the magnetic fields considered, the 1u state exhibits a pronounced minimum in the potential energy curve, but only in those magnetic fields for which the global minimum of energy at finite Req is below the total energy of the Hydrogen atom in the ground state (see Fig. 3 for example for B = 1a.u) the system is considered to be stable. The deepest well in the parallel configuration occurs for a uniform magnetic field of ∼ 2 a.u. that represents the maximal stability of the system (maximum of dissociation energy as a function of the magnetic field) (see Fig. 2).
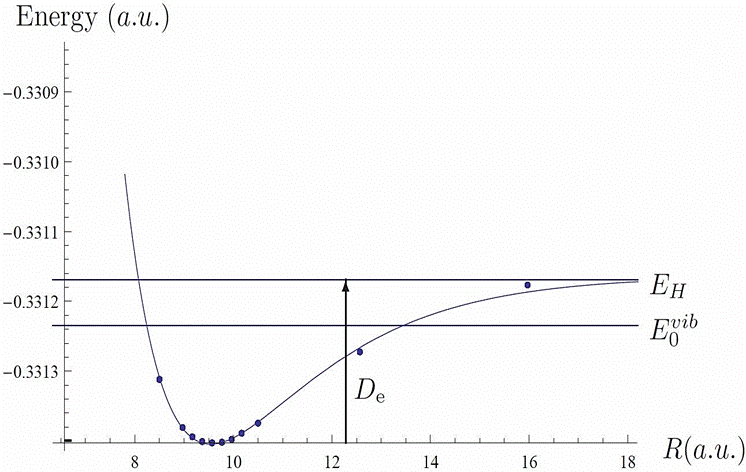
Figure 3 Total energy (dots) of the 1u state of
4.3. Vibrational states
A natural question concerning the stability of molecular systems is related to the existence of at least one nuclear vibrational state. In order to answer this question, for B = 1a.u. we carried out variational calculations for different fixed values of the internuclear distance R and built the potential curve corresponding to the 1u state. In Fig. 3 we show that such potential curve fits reasonably well a Morse potential. Using this fit, we computed the energy of the first vibrational state obtaining
5. Inclined Configurations
5.1. Stability of 1u state: Critical Angles
In the present study, we also considered the analysis of inclined configurations 0° < θ < 90° using the trial function (9). It is important to mention that for arbitrary inclinations of the magnetic field there are almost no references in the literature. The only exception is 26 where the qualitative description is very different from the behavior obtained in the present study. We consider that such differences do not allow for a direct comparison with the present resultsv and that independent calculations are needed in order to resolve this disagreement.
Our variational results are presented in Tables III and IV for the magnetic fields B = 0.1 a.u. and B = 1 a.u. respectively.
Table III Total energy ET, and equilibrium distance Req for the state 1u at different orientations θ of the magnetic field with respect to the molecular axis for the magnetic field B = 0.1a.u. We estimate that the uncertainty in Req is ∆ ≃ 0.05a.u. due to the fact that the potential well is too flat. The total energy of the ground state of Hydrogen atom at B = 0.1 a.u. is −0.497527 a.u.
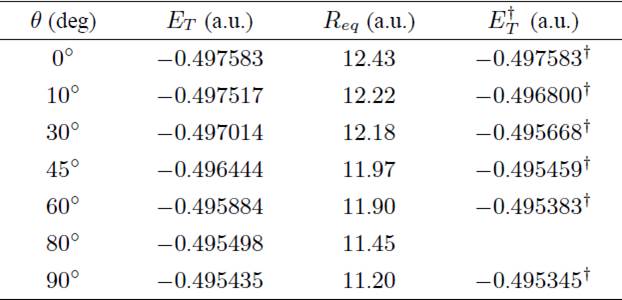
† results from 1.
Table IV Total energy ET, and equilibrium distance Req for the state 1u at different orientations θ of the magnetic field with respect to the molecular axis for the magnetic field B = 1a.u. We estimate that the uncertainty in Req is ∆ ≃ 0.05a.u. due to the fact that the potential well is too flat. The total energy of the ground state of Hydrogen atom at B = 1a.u. is −0.331169a.u.

† results from 1.
As we expected the maximal symmetry configurations are found to correspond to the extremals of energy: the parallel configuration is the optimal configuration of total energy, while the perpendicular configuration corresponds to the maximum of total energy (though it also corresponds to the most compact configuration).
The behavior of the total energy of 1u state of (ppe)-system for both representative magnetic fields is monotonously increasing as a function of the inclination angle θ of the magnetic field, while the equilibrium distance Req decreases monotonically (see Tables III, IV and Figs. 4, 5).
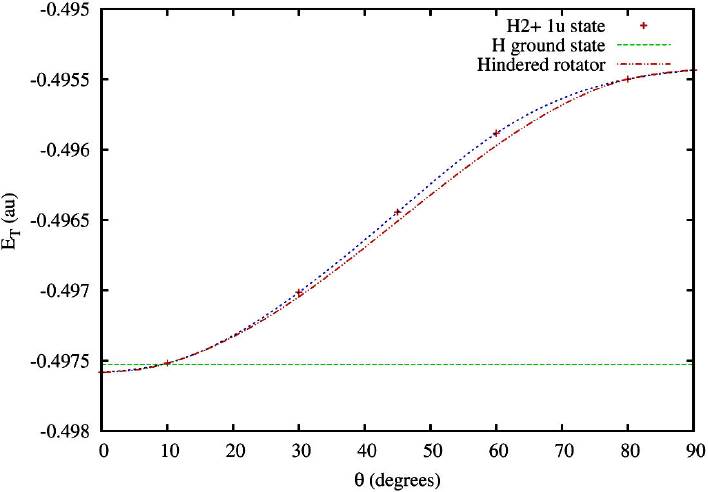
Figure 4 Total energy ET of the 1u state of
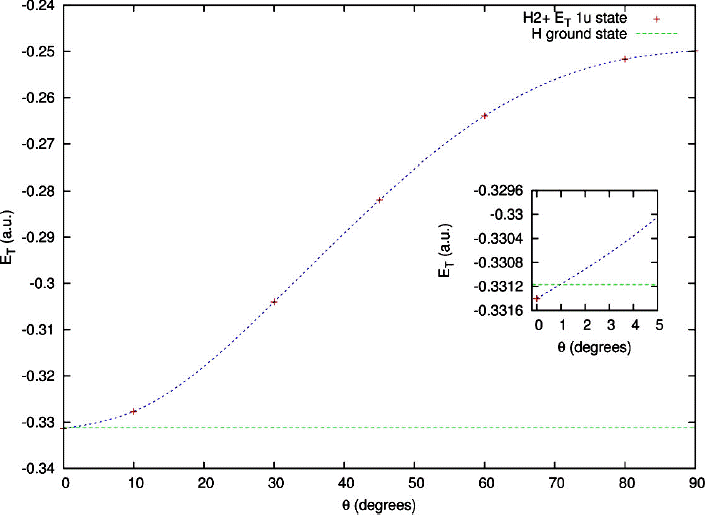
Figure 5 Total energy ET of the 1u state of
For both magnetic fields, the 1u state of the (ppe)-system becomes unstable towards dissociation
It is worth to observe from Fig. 4 that our variational results as a function of the inclination angle θ fit well at a hindered rotator model
where ∆V (R) = V (R,90°)−V (R,0°) is the barrier height for a given value of R. Such behavior would allow us to make a similar rotational analysis as it was done in 28 for the ground state 1g (this will be done elsewhere).
Using our variational results, it is possible to construct a surface of energy as a function of the molecular distance R and the magnetic field orientation θ (see Fig. 6 for B = 1a.u). The potential energy surface appears smooth and without indications to any other local minimum.
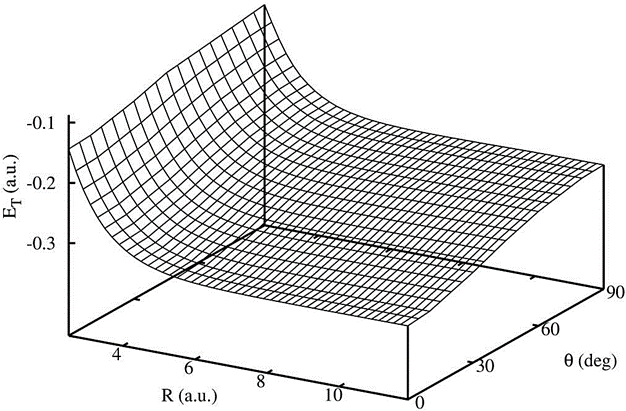
Figure 6 Total energy ET (in a.u.) of the 1u state of
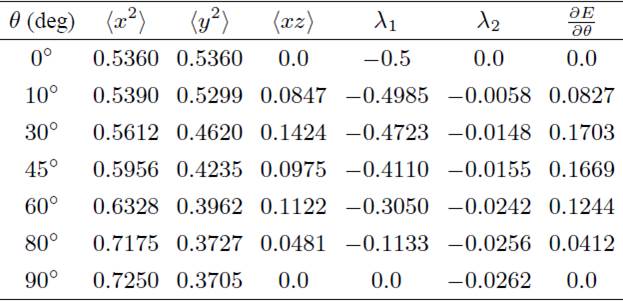
Additionally, we made an analysis of the behavior of the expectation values 〈x2〉, 〈y2〉, 〈xz〉 as well the gauge parameters λ1,2, with respect to the orientation angle θ for a magnetic field B = 1a.u. (see Fig. 7 and Table V) as obtained with the trial function (9). From these values, we can compute the variation of the total energy of the 1u state through Eq. (10). Both expectation values hx2i and hy2i increase/decrease monotonously as a function of the inclination angle. On the other side, the expectation value hxzi vanishes in the configurations θ = 90° due to the symmetry z → −z. This corroborates the result predicted by the Hellman-Feynman theorem, i.e. the variation of the total energy becomes zero only in the configurations of maximal symmetry. The analysis also confirms that the optimal gauge for the parallel configuration θ = 0° corresponds to the symmetric gauge, while for the perpendicular configuration θ = 90°, the Landau Gauge seems to be more adequate.
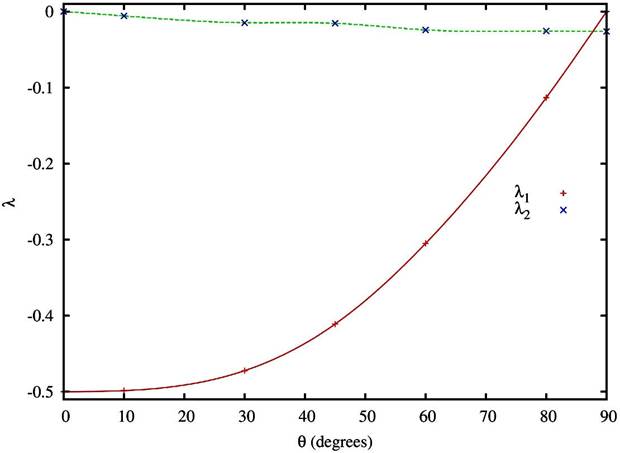
Figure 7 Optimal gauge variational parameters λ as a function of the orientation θ for the magnetic field B = 1 a.u. In the parallel configuration (θ = 0°) the optimal gauge corresponds to the symmetric gauge (λ1 = −1/2, λ2 = 0). In the perpendicular configuration (θ = 90°) the optimal gauge is very close to the Landau gauge (λ1 = 0, λ2 = −0.08).
6. Conclusions
We found a range of magnetic fields where the 1u state of
From an astrophysics point of view, the stability of the 1u state can be of relevance for the analysis of the spectra of white dwarfs. For example, in the magnetic field B = 1a.u. the energy corresponding to the transition between the two lowest states of
7. Note added in proof
While this manuscript was under consideration the authors performed an analysis for the ground state 1g in magnetic fields 0.1a.u. ≤ B ≤ 1 a.u., using a linear superposition of three functions of the type (6) and found an improvement in the variational energy (for intermediate angles 0° < θ < 90°) which is in excellent agreement with the hindered rotor model approximation (14) used in the reference 28. It is worth to mention that the agreement between the hindered rotor model and the variational results using the functions of the type (6) is much better in the case of the ground state 1g. This results will be reported elsewhere.











 nueva página del texto (beta)
nueva página del texto (beta)