Introducción
Se propone un método para prediseñar o rehabilitar una red de alcantarillado pluvial en una zona urbana. El método consta de dos partes, en una se proponen varias opciones de conexión de las tuberías por las calles (trazo de la red de tuberías) y en la segunda, se obtienen los diámetros y las pendientes para cada uno de los conductos de la red para que sea mínima la suma de los costos de adquisición de las tuberías y de la excavación necesaria para su instalación, de modo que se cumpla con las condiciones de velocidad y de llenado de las tuberías, así como las normas constructivas establecidas para esta clase de redes donde se asegure un funcionamiento hidráulico adecuado.
El método considera varios arreglos de redes y escoge uno de ellos. Por razones de economía, en las redes de alcantarillado propuestas se busca que las tuberías tengan una pendiente similar a la de la superficie del terreno. El trazo se inicia en uno o varios sitios de vertido de la red; a partir de los cuales se definen las conexiones de colectores y emisores.
También, se toma en cuenta la profundidad a la cual quedan desplantados los conductos, de manera que la suma de los costos de excavación de la instalación y los de adquisición de las tuberías sea lo más baja posible. Se presenta la aplicación a un caso real. Además, se revisa que el funcionamiento hidráulico de la red prediseñada cumpla con los requisitos de tipo hidráulico establecidos en los manuales de diseño para esta clase de redes.
En el método se busca que el flujo de agua ocupe 80 % de la sección transversal de las tuberías, para que el caudal se aproxime al más grande posible que ocurre en tuberías de sección circular; además, con ello también queda un espacio libre para que no se obstruyan por sólidos que podrían desplazarse con el agua.
Desarrollo
Para el prediseño de las redes de drenaje pluvial se requiere de información hidrológica para un periodo de retorno de diseño específico. Por ello, se consideran los registros de estaciones pluviométricas cerca y dentro de la zona donde se construirá. Se escogen las estaciones con más años de datos de lluvia diaria. También se revisa la homogeneidad y estacionalidad (Salas & Obeysekera, 2014) de los registros mencionados para realizar análisis estadísticos confiables.
Para cada estación pluviométrica se encuentra lluvia diaria máxima en cada año para obtener los parámetros de varias funciones de probabilidad que se aproximan a la distribución anual de estas lluvias.
Para estimar la variación horaria de la precipitación diaria se puede recurrir a distintos procedimientos como el que se basa en la relación de convectividad (R) entre la lluvia máxima anual en 1 hora y la media de las lluvias máximas anuales diarias (Reich, 1963). Dicha relación se presenta en la Figura 1, donde se toma en cuenta la precipitación de una hora y periodo de retorno de dos años, el número promedio con lluvia anual y la media de las lluvias máximas anuales.

Figura 1 Relación de convectividad (R) entre la lluvia máxima anual en 1 hora y la media de las lluvias máximas anuales diarias
Se considera que el valor de la relación R se mantiene constante para otros periodos de retorno, por lo que lámina de lluvia de una hora para el periodo de retorno T:
Para disponer de los datos necesarios para dibujar las curvas altura de lluvia-duración-periodo de retorno (hp-d-T) se utiliza la siguiente ecuación:
Donde:
d = duración de la lluvia (horas).
hp1h T = lluvia de una hora para el periodo de retorno (T).
hp24h T = lluvia de 24 horas para el periodo de retorno (T).
Para duraciones de 5, 10, 15, 30 y 45 minutos se considera que
La intensidad de la lluvia se estima a partir de las alturas de lluvia mediante:
El escurrimiento se puede obtener con la fórmula Racional que supone que la intensidad de lluvia comienza instantáneamente y continua indefinidamente hasta alcanzar el tiempo de concentración.
Para obtener los hidrogramas se empleó el hidrograma unitario adimensional propuesto por el Soil Conservation Service de Estados Unidos (Mockus, 1957) que se muestra en la Figura 2.
El hidrograma de escurrimiento queda definido al multiplicar los valores de las ordenadas y las abscisas, por el gasto y tiempo de pico, por
El Manual de Agua Potable, Alcantarillado y Saneamiento (MAPAS) (Conagua, 2019) señala que en las redes de drenaje urbano se deben cumplir las siguientes restricciones:
a) Para evitar depósitos de sólidos dentro de las tuberías o disminuir los posibles desgastes de la pared interior por rozamiento, la velocidad media del flujo (V) dentro del conducto debe ser mayor a 0.30 m/s y menor a 3.0 m/s.
b) Se considera que el flujo es uniforme para relacionar al diámetro del conducto y la pendiente con el caudal.
c) Se busca que la profundidad hidráulica (y) del flujo del líquido en las tuberías ocupe 80 % de su diámetro (D), para aproximarse al máximo caudal de conducción con flujo uniforme a superficie libre en tubería de sección circular (Figura 3).
d) La profundidad en el terreno a la que se instalan las tuberías debe ser mayor o igual a una mínima (colchón) establecida para protegerlas contra cargas vivas en la superficie del terreno (Figura 4).
e) En la unión de tuberías, el diámetro de la tubería aguas abajo debe ser igual o mayor al de la tubería agua arriba.
f) Se considera que, en la unión de tuberías consecutivas, la elevación de la clave de la tubería agua abajo sea igual a la elevación de la clave tubería aguas arriba para evitar escalones.

Figura 3 Relaciones entre variables hidráulicas de una tubería de sección circular con flujo uniforme a superficie libre (Chow, 1959)
El procedimiento propuesto para el prediseño de la red de drenaje pluvial urbana se basa en la idea principal de asociar a cada diámetro de tubería con una pendiente (S) para su plantilla, de acuerdo con el gasto (Q) del líquido que fluye en su interior. Para estimar dicha pendiente se considera que este flujo es a superficie libre y uniforme, por lo que la profundidad hidráulica o tirante (y) es del orden de 80 % del diámetro (D) con la intención de aproximarse a la capacidad máxima de conducción de tuberías de sección transversal circular (Figura 3), lo que de acuerdo con la fórmula de Manning (Chow, 1959) cumple con la siguiente ecuación:
El área hidráulica (A) dentro del conducto de sección circular para una profundidad hidráulica igual a 0.80 D, se obtiene a partir de la relación:
Así, la velocidad media (V) del flujo se obtiene al dividir al caudal entre el área hidráulica.
Para asegurarse que el flujo de agua en el interior de los conductos sea subcrítico, el caudal debe ser menor al caudal crítico
De este modo, a cada diámetro de tubería de la red se relaciona con el gasto, la pendiente y la velocidad media.
En las redes de drenaje las tuberías se conectan de manera que donde termine una, se ligue con solo una tubería, formando una secuencia de conducto que se denomina ramal. Es importante tener en cuenta que cada ramal de la red, inicia con una tubería en la zona de mayor elevación topográfica y dicha tubería requiere que su profundidad de instalación sea tal, que la clave de su extremo aguas arriba cumpla con una profundidad mínima para evitar que se dañe por cargas vivas sobre el terreno que está encima de ella.
El método de prediseño de la red de drenaje pluvial urbana requiere de la siguiente información:
a) El trazo de la red. De acuerdo con la configuración de las calles, las elevaciones topográficas y el sitio de desalojo del agua de la red, se proponen los pozos de visita y las conexiones entre conductos de la red de drenaje.
b) Diámetros comerciales elegibles para las tuberías de la red.
c) Coeficientes de rugosidad del material de las tuberías.
d) Costos de excavación por metro cúbico de acuerdo con el tipo de material de la zona donde se instalarán las tuberías de la red de drenaje.
e) Costos de adquisición de la tubería por unidad de longitud (metro) de acuerdo con su diámetro y material.
El método de prediseño consta de dos partes principales; en la primera, se propone el trazo de la red y en la segunda, se emplea un algoritmo genético para obtener los diámetros, las pendientes de las tuberías y la profundidad a que deben instalarse, de modo que la suma de los costos de adquisición y excavación de instalación de los conductos sea mínima, además de que se cumplan las condiciones hidráulicas y constructivas impuestas.
Para definir el trazo de la red se emplea un grafo, que consiste en un esquema que muestra un conjunto de sitios (nodos) unidos por líneas (arcos). Cuando en cada arco se considera la distancia entre los nodos de sus extremos, es posible escogerlos buscando que los nodos se unan con uno específico y con la distancia más corta entre ellos. Esto puede realizarse con algoritmos de la teoría de redes de investigación de operaciones.
En el caso de la red de drenaje, los nodos y arcos corresponden respectivamente a los pozos de visita y a las tuberías. Además, se considera que los arcos tienen un sentido de recorrido, que va desde el pozo con mayor elevación topográfica en su brocal hacia el pozo de menor elevación de este elemento. En este artículo se planteó una variante en el algoritmo de Dijkstra (1959) donde se busca que la suma de las longitudes de los arcos sea la menor posible.
Para obtener el trazo de la red se comienza por llamar nodo actual al de salida de la red y a los restantes como nodos no visitados; posteriormente se emplea una rutina donde se van eligiendo los pozos de visita desde aguas abajo hacia aguas arriba y consiste en los pasos siguientes:
Se selecciona el nodo no visitado con menor elevación topográfica de su brocal, el cual tiene un arco de conexión que llega a él con menor longitud.
El nodo y arco que fueron elegidos son marcados como nodo y arco visitado.
Cuando no quedan nodos visitados por seleccionar se continúa con el paso 4; de otro modo, se escoge como nodo actual al nodo no visitado, ya que tiene la menor elevación topográfica en su brocal (si hubiese más de uno se escoge el más cercano) y se regresa al paso 1.
Se identifican las secuencias de arcos (ramales de la red o rutas) desde los nodos de menor elevación topográfica hacia los nodos de mayor elevación, hasta llegar a un nodo que ya no tiene conexiones dirigidas a él.
En cada nodo de la red se incorpora el caudal de pico del área tributaria que le corresponde y de acuerdo con los ramales, estos caudales se acumulan para asignarlos como el caudal máximo que fluye en cada tubería de la red de drenaje. En el caso de aplicación del método de prediseño de la red, se muestran con cierto detalle los pasos que condujeron al trazo y los caudales máximos de cada tubería.
Los algoritmos genéticos pueden emplearse para optimar funciones. Están basados en el proceso de supervivencia de los organismos vivos. En el transcurso de varias generaciones, las poblaciones evolucionan de acuerdo con los principios de la selección natural y se mantienen los más fuertes de acuerdo con postulados por Darwin. Por imitación a este proceso, con los algoritmos genéticos se llega a obtener el máximo o mínimo global de funciones de algunas variables que cumplen con diferentes restricciones específicas.
El algoritmo genético se instituye como un método repetitivo, el cual considera que cierto número de valores de la función a optimizar corresponde a los individuos de la población de una generación y crea a partir de ellos, otra población con sus descendientes, que son individuos más fuertes. Luego se reemplaza a los individuos de la generación original con descendientes para establecer de este modo un proceso repetitivo y con el transcurso de las generaciones, incrementar la fortaleza en las poblaciones descendientes.
En el algoritmo genético se asigna cierto grado de fortaleza a cada individuo de la población de una generación mediante una función que se conoce como aptitud donde se identifica al más fuerte. Al cabo de varias generaciones se van teniendo individuos más aptos y se encuentra al de mayor aptitud entre ellos (Fuentes et al, 2004). En el caso del prediseño, la red de drenaje por cada individuo corresponde a un conjunto de tuberías que forman parte de una red de drenaje y el individuo más apto a la red de drenaje que tiene el menor costo de adquisición e instalación, que además, cumple con las condiciones hidráulicas y constructivas de interés (Hernández, 2007).
Como para cada una de las tuberías de la red se conoce el gasto que circula dentro de ella, es posible asignarle un diámetro y una pendiente. Posteriormente, se consideran las tuberías que forman parte de cada ramal de la red para fijar la profundidad a la que se instalarán las tuberías que lo conforman, atendiendo a la restricción de profundidad mínima, con lo cual, queda establecido el prediseño de la red de drenaje que resulta ser un individuo de la población de una generación.
La aptitud de un prediseño de red de tuberías se considera igual al recíproco de la suma de los costos de adquisición de las tuberías y de excavación. Posteriormente, de todas las redes de una generación se localiza la que tiene la mayor aptitud.
El método comienza a partir de una población inicial formada por un conjunto de individuos escogidos aleatoriamente. En el caso del drenaje, correspondería a un conjunto de redes de tuberías donde el diámetro de cada conducto se escoge de forma aleatoria de una lista de diámetros de tuberías disponibles en el comercio. De acuerdo con su gasto máximo que circula en cada tubería, se asigna aleatoriamente un diámetro, el cual tiene asociados, una pendiente y la profundidad del fondo del extremo aguas arriba de la tubería. Luego, con el diámetro pendiente y la elevación de la clave de su extremo aguas arriba de las tuberías se calcula el volumen de la excavación requerida para la instalación.
Después de varias generaciones, se encuentra que la máxima aptitud de las generaciones sucesoras ya no cambia, lo cual significa que se hizo el prediseño óptimo de la red, ya que quedaron definidos los diámetros y pendientes de las tuberías, así como las profundidades en que se ubicarán, de manera que la suma mínima de los costos de adquisición y excavación cumplen con las restricciones hidráulicas y constructivas establecidas como requisito. La función de aptitud se planteó como el recíproco de la suma de los costos de adquisición
Donde K es una constante que permite contar con los valores de la función objetivo, fáciles de apreciar y, sobre todo, reducen el error de redondeo de las cifras decimales.
Para la mezcla de individuos se usó el proceso de selección de aptitud proporcional o ruleta. Se empleó una probabilidad de cruza igual a 0.7 considerando que, para el problema en cuestión, la probabilidad de mutación igual a 0.02 era la que mejor se apegaba al funcionamiento hidráulico. Estos valores se fijaron de modo que se lograra tener una variedad adecuada de resultados (Fuentes et al., 2011).
Discusión y análisis de resultados
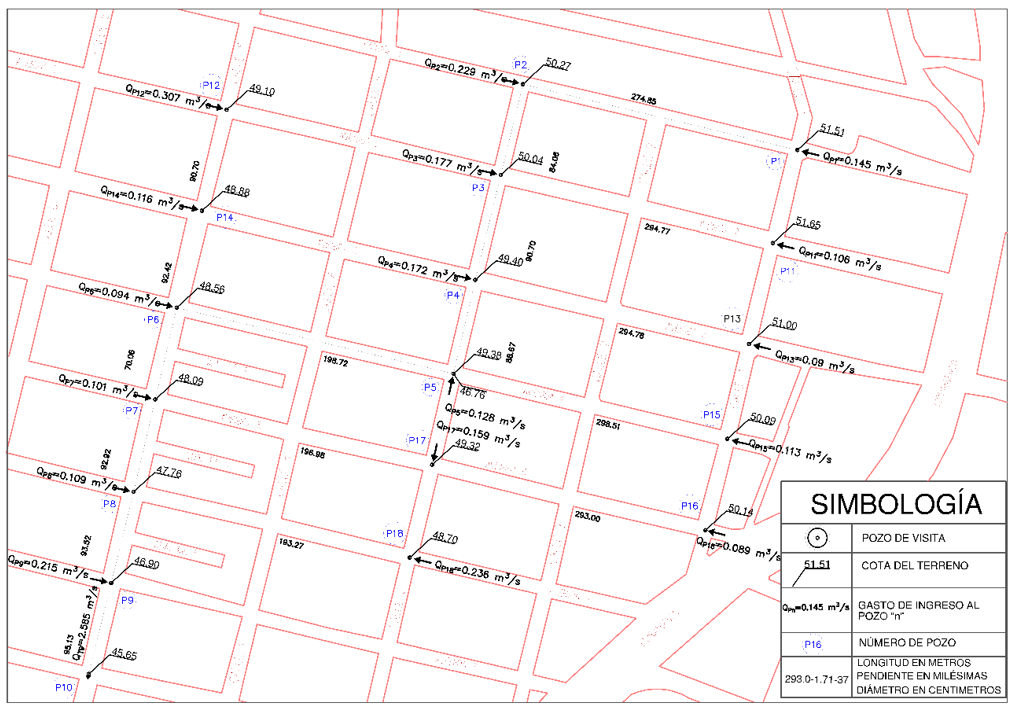
El método propuesto se aplicó a un caso real. Se escogió la localidad San Reforma del municipio de Tapachula, Chiapas en México. En la Figura 4 se muestra la zona en estudio donde se señalaron los pozos de visita y las calles donde podrían instalarse las tuberías de la red de drenaje pluvial.
Se consideró la siguiente información:
a) El tiempo de concentración, las áreas (tributarias) que reciben la lluvia que ingresa a cada uno de los pozos de visita y los coeficientes de escurrimiento correspondiente a dichas áreas.
b) Los hidrogramas de entrada a los pozos de visita del agua calculados a partir de la lluvia con periodo de retorno de 10 años. Para ello, se tomó en cuenta la intensidad, duración y el periodo de retorno de la precipitación en cada área tributaria de la red de drenaje.
c) Se emplearon los registros de lluvia diaria de 5 estaciones climatológicas que cubren la zona de influencia para la red de drenaje pluvial.
d) Se completaron los datos faltantes de los registros y se revisó que los registros en las estaciones fueran homogéneas y estacionarias.
e) Con las láminas de lluvia diaria se obtuvieron las láminas máximas anuales y se ajustaron los parámetros de varias funciones de probabilidad. Para escoger la de mejor ajuste, se obtuvo el mínimo error estándar de ajuste (EEA).
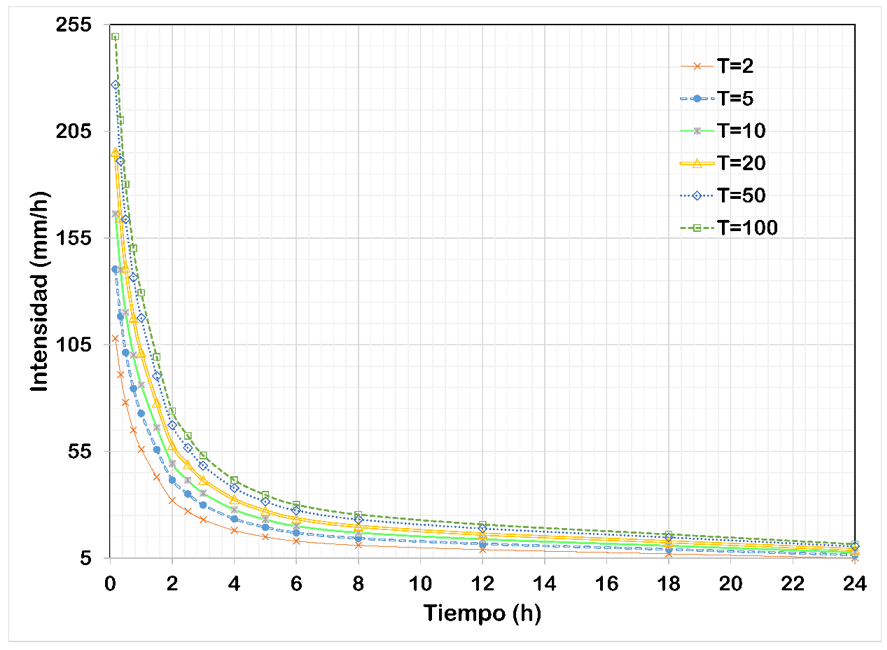
Se obtuvieron las curvas intensidad-duración periodo de retorno de la zona en estudio que se muestran la Figura 5.
De acuerdo con las características fisiográficas de la zona se estimó que en la zona en estudio en el tiempo pico es de 3.25 horas y se encontró que para el periodo de retorno de 10 años la intensidad de la lluvia es de 41.7 mm/h.
Se obtuvieron los gastos máximos en cada área de la zona de estudio para un periodo de retorno de 10 años, con el método racional, considerando que el coeficiente de escurrimiento es de 0.62.
En la Tabla 1 se presentan las áreas tributarias de la zona de estudio de Tapachula, Chiapas y los gastos máximos de ingreso a sus pozos de visita.
Tabla 1 Áreas tributarias y caudales de pico de entrada a los pozos de visita
| Área tributaria |
Superficie (ha) |
Gasto pico (m3/s) |
Área tributaria |
Superficie (ha) |
Gasto pico (m3/s) |
|---|---|---|---|---|---|
| 1 | 2.02 | 0.145 | 10 | 1.77 | 0.128 |
| 2 | 3.17 | 0.229 | 11 | 1.30 | 0.094 |
| 3 | 1.47 | 0.106 | 12 | 1.23 | 0.089 |
| 4 | 2.45 | 0.177 | 13 | 2.20 | 0.159 |
| 5 | 4.26 | 0.307 | 14 | 1.40 | 0.101 |
| 6 | 1.24 | 0.090 | 15 | 3.27 | 0.236 |
| 7 | 2.38 | 0.172 | 16 | 1.50 | 0.110 |
| 8 | 1.61 | 0.116 | 17 | 2.98 | 0.215 |
| 9 | 1.56 | 0.113 | 18 | 3.27 | 0.236 |
Con el hidrograma unitario adimensional del Soil Conservation Service de Estados Unidos (Mockus, 1957) se obtuvieron los hidrogramas del escurrimiento de ingreso a cada pozo de visita que se muestran en Figura 6.
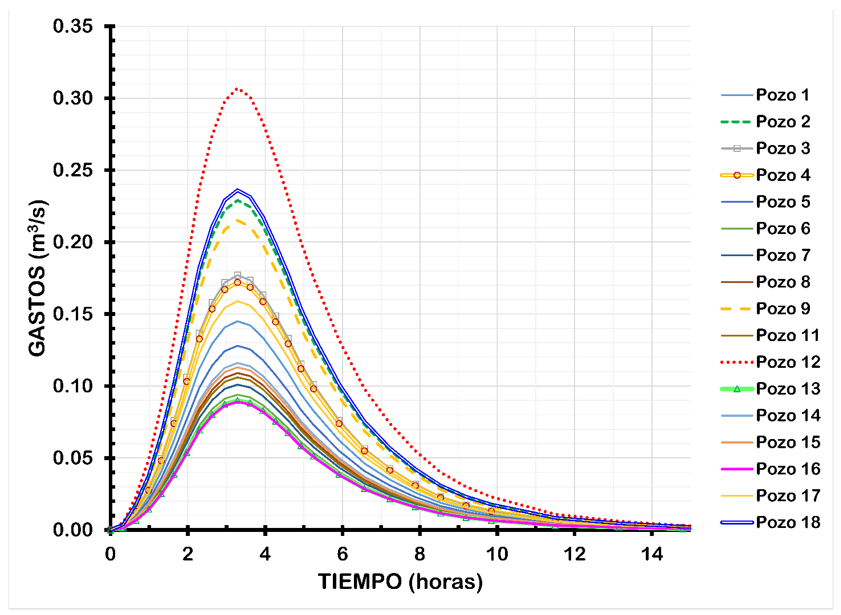
Figura 6 Hidrogramas del escurrimiento para el periodo de retorno de 10 años que ingresan a los pozos de visita
A partir de la ubicación de los pozos de visita en el plano urbano de la zona en estudio (Figura 4) y de las calles por donde podrían instalarse las tuberías, se formó el grafo mostrado en la Figura 5. En el siguiente grafo se muestran los arcos que unen a los nodos (pozos de visita) como segmentos dirigidos que van desde el pozo de visita con la cota del umbral más alta hacia el pozo de visita con una cota de umbral más baja (Figura 7).
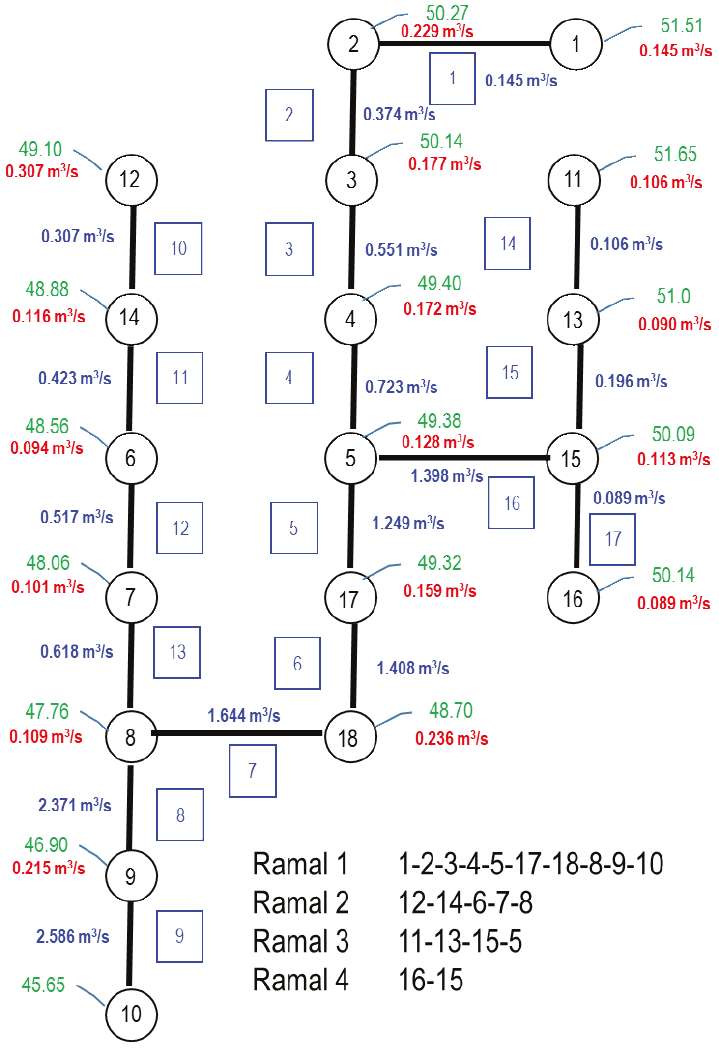
El proceso para obtener el trazo de la red de drenaje pluvial urbana se hace de aguas abajo hacia aguas arriba. Se comenzó con el nodo 10, que solo tenía ligado el 9, luego se pasó al nodo 8 porque era el único asociado al 9. Quedaron como visitados los nodos 10, 9 y 8. El nodo no visitado con la menor elevación fue el 7, que se escogió y pasó a ser nodo visitado. El siguiente nodo con menor elevación no visitado fue el 6, el cual se cambió a visitado. Le siguió el 18 como no visitado, y se ligó al 8 por ser el más cercano de los visitados. De esta manera se fueron ligando los nodos 6, 14, 12, 17, 5, 4, 3, 15, 13, 6, 2, 1 y el 11. Después, se formaron los 4 ramales siguientes: El ramal 1 con los nodos 1, 2, 3, 4, 5, 17, 18, 8, 9 y 10. El ramal 2 con los nodos 12, 14, 6, 7 y 8. El ramal 3 con los nodos 11, 13, 15 y 5. Por último, el ramal 4 con los nodos 16 y 15. En los cuadros de la Figura 7 se señala el orden en que fueron obtenidos los tramos de la red.
En la Figura 8 se muestra el trazo de la red de drenaje pluvial que se basa el algoritmo genético para obtener su prediseño óptimo.
Los gastos más grandes que circulan en cada tubería de la red de drenaje que se consignan en la Tabla 2 se obtuvieron al sumar los caudales pico que ingresaron por los pozos de visita de acuerdo con el trazo de la red mostrado en la Figura 8.
Tabla 2 Gastos que fluyen en las tuberías de la red de drenaje pluvial
| Ramal | Tubería | Pozo | Longitud (m) | Cota terreno | Gasto (m3/s) | ||
|---|---|---|---|---|---|---|---|
| Inicial | Final | Inicial (m) | Final (m) | ||||
| 1 | 1 | P1 | P2 | 274.90 | 51.51 | 50.27 | 0.145 |
| 1 | 2 | P2 | P3 | 84.10 | 50.27 | 50.14 | 0.374 |
| 1 | 3 | P3 | P4 | 90.70 | 50.14 | 49.40 | 0.551 |
| 1 | 4 | P4 | P5 | 88.70 | 49.40 | 49.38 | 0.723 |
| 1 | 5 | P5 | P17 | 70.06 | 49.38 | 49.32 | 1.249 |
| 1 | 6 | P17 | P18 | 92.99 | 49.32 | 48.70 | 1.408 |
| 1 | 7 | P18 | P8 | 193.00 | 48.70 | 47.76 | 1.644 |
| 1 | 8 | P8 | P9 | 93.50 | 47.76 | 46.90 | 2.371 |
| 1 | 9 | P9 | P10 | 95.10 | 46.90 | 45.65 | 2.586 |
| 2 | 10 | P12 | P14 | 90.70 | 49.10 | 48.88 | 0.307 |
| 2 | 11 | P14 | P6 | 92.40 | 48.88 | 48.56 | 0.423 |
| 2 | 12 | P6 | P7 | 70.10 | 48.56 | 48.06 | 0.517 |
| 2 | 13 | P7 | P8 | 92.90 | 48.06 | 47.76 | 0.618 |
| 3 | 14 | P15 | P5 | 298.50 | 50.09 | 49.38 | 0.106 |
| 3 | 15 | P11 | P13 | 90.10 | 51.65 | 51.00 | 0.196 |
| 3 | 16 | P13 | P15 | 88.74 | 51.00 | 50.09 | 0.398 |
| 4 | 17 | P16 | P15 | 70.43 | 50.14 | 50.09 | 0.089 |
Se emplearán tuberías de polietileno corrugado de alta densidad (PEAD). Los diámetros comerciales elegibles para las tuberías se consignan en la Tabla 3. Para todas las tuberías el coeficiente de rugosidad de la fórmula de Manning es de 0.01 s/m1/3.
Tabla 3 Diámetros comerciales y costos por metro para las tuberías la red de drenaje pluvial
| Diámetro (m) | Costo ($/m) |
|---|---|
| 0.37 | 450 |
| 0.45 | 510 |
| 0.61 | 630 |
| 0.76 | 845 |
| 0.91 | 1,250 |
| 1.07 | 1,610 |
| 1.22 | 2,000 |
| 1.52 | 3,210 |
| 1.83 | 4,620 |
| 2.13 | 6,120 |
| 2.44 | 7,944 |
De acuerdo con el caudal máximo conducido en cada tubería y el funcionamiento hidráulico a superficie libre con flujo uniforme y profundidad hidráulica se escogieron los diámetros comerciales de las tuberías que cumplirían con las condiciones de velocidad media y flujo subcrítico que se consignan en la Tabla 4.
Tabla 4 Diámetros elegibles para cada una de las tuberías de la red de drenaje pluvial
| Ramal | Tubería | Diámetros elegibles (m) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.45 | 0.61 | 0.76 | 0.76 | 0.76 | 0.76 | 0.76 | 0.76 |
| 1 | 2 | 0.61 | 0.76 | 0.91 | 1.07 | 1.22 | 1.22 | 1.22 | 1.22 |
| 1 | 3 | 0.76 | 0.91 | 1.07 | 1.22 | 1.52 | 1.52 | 1.52 | 1.52 |
| 1 | 4 | 0.76 | 0.91 | 1.07 | 1.22 | 1.52 | 1.83 | 1.83 | 1.83 |
| 1 | 5 | 1.07 | 1.22 | 1.52 | 1.83 | 2.13 | 2.44 | 2.44 | 2.44 |
| 1 | 6 | 1.07 | 1.22 | 1.52 | 1.83 | 2.13 | 2.44 | 2.44 | 2.44 |
| 1 | 7 | 1.07 | 1.22 | 1.52 | 1.83 | 2.13 | 2.44 | 2.44 | 2.44 |
| 1 | 8 | 1.22 | 1.52 | 1.83 | 2.13 | 2.44 | 2.44 | 2.44 | 2.44 |
| 1 | 9 | 1.52 | 1.83 | 2.13 | 2.44 | 2.44 | 2.44 | 2.44 | 2.44 |
| 2 | 10 | 0.61 | 0.76 | 0.91 | 1.07 | 1.22 | 1.22 | 1.22 | 1.22 |
| 2 | 11 | 0.61 | 0.76 | 0.91 | 1.07 | 1.22 | 1.22 | 1.22 | 1.22 |
| 2 | 12 | 0.76 | 0.91 | 1.07 | 1.22 | 1.52 | 1.52 | 1.52 | 1.52 |
| 2 | 13 | 0.76 | 0.91 | 1.07 | 1.22 | 1.52 | 1.52 | 1.52 | 1.52 |
| 3 | 14 | 0.37 | 0.45 | 0.61 | 0.61 | 0.61 | 0.61 | 0.61 | 0.61 |
| 3 | 15 | 0.45 | 0.61 | 0.76 | 0.91 | 0.91 | 0.91 | 0.91 | 0.91 |
| 3 | 16 | 0.61 | 0.76 | 0.91 | 1.07 | 1.22 | 1.22 | 1.22 | 1.22 |
| 4 | 17 | 0.37 | 0.45 | 0.61 | 0.61 | 0.61 | 0.61 | 0.61 | 0.61 |
En la Tabla 5 se muestran algunos resultados del algoritmo genético, se presentan los mayores valores de la función de aptitud, la suma de los costos de excavación y de adquisición de las tuberías para el individuo más apto de cada generación.
Tabla 5 Proceso de aproximación al costo total mínimo de la red de drenaje pluvial que cumple con las condiciones hidráulicas y constructivas
| Generación | Individuo | Función aptitud |
Costo excavación (pesos) |
Costo tuberías (pesos) |
Costo total (pesos) |
|---|---|---|---|---|---|
| 1 | 1 | 0.2079 | 1,887,311 | 2,922,411 | 4,809,722 |
| 1 | 4 | 0.223 | 1,750,509 | 2,733,877 | 4,484,386 |
| 1 | 9 | 0.2245 | 1,732,965 | 2,721,958 | 4,454,923 |
| 1 | 38 | 0.2341 | 1,697,728 | 2,573,819 | 4,271,547 |
| 2 | 13 | 0.2604 | 1,491,587 | 2,348,175 | 3,839,762 |
| 3 | 39 | 0.2744 | 1,421,644 | 2,222,415 | 3,644,059 |
| 4 | 22 | 0.2799 | 1,397,988 | 2,174,499 | 3,572,487 |
| 5 | 24 | 0.2902 | 1,352,795 | 2,092,998 | 3,445,793 |
| 9 | 20 | 0.2984 | 1,325,277 | 2,026,416 | 3,351,693 |
| 11 | 30 | 0.2999 | 1,329,839 | 2,005,009 | 3,334,848 |
| 14 | 21 | 0.3013 | 1,313,255 | 2,005,192 | 3,318,447 |
| 32 | 34 | 0.3055 | 1,298,705 | 1,974,331 | 3,273,036 |
| 35 | 28 | 0.3059 | 1,295,398 | 1,973,151 | 3,268,549 |
| 38 | 11 | 0.3067 | 1,291,386 | 1,968,925 | 3,260,312 |
Nótese que el ahorro entre el costo de la primera alternativa y la última es de 32 %, ((4’809,722 - 3’260312) / 4’809,722 = 0.32).
En la Tabla 6 se muestran las principales características del arreglo de red de drenaje pluvial con el método propuesto.
Tabla 6 Características de la red de drenaje pluvial urbana para el periodo de retorno de 10 años
| Tubería | Pozo inicial |
Pozo final |
Longitud (m) |
Caudal (m3/s) |
Diámetro (m) |
Colchón inicial (m) |
Colchón final (m) |
Elevación fondo inicial (m) |
Elevación fondo final (m) |
Pendiente (m/m) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 274.90 | 0.145 | 0.45 | 2.35 | 1.55 | 49.16 | 48.72 | 0.0016 |
| 2 | 2 | 3 | 84.10 | 0.374 | 0.61 | 1.71 | 1.76 | 48.56 | 48.38 | 0.0021 |
| 3 | 3 | 4 | 90.70 | 0.551 | 0.76 | 2.47 | 1.86 | 47.67 | 47.54 | 0.0014 |
| 4 | 4 | 5 | 88.70 | 0.723 | 0.76 | 1.86 | 2.06 | 47.54 | 47.32 | 0.0024 |
| 5 | 5 | 17 | 70.06 | 1.249 | 1.07 | 2.37 | 2.39 | 47.01 | 46.93 | 0.0012 |
| 6 | 17 | 18 | 92.99 | 1.408 | 1.07 | 2.65 | 2.17 | 46.67 | 46.53 | 0.0015 |
| 7 | 18 | 8 | 193.00 | 1.644 | 1.07 | 2.72 | 2.17 | 45.98 | 45.59 | 0.0020 |
| 8 | 8 | 9 | 93.50 | 2.371 | 1.22 | 2.98 | 2.32 | 44.78 | 44.58 | 0.0021 |
| 9 | 9 | 10 | 95.10 | 2.586 | 1.52 | 3.80 | 2.62 | 43.1 | 43.03 | 0.0008 |
| 10 | 12 | 14 | 90.70 | 0.307 | 0.61 | 1.80 | 1.71 | 47.3 | 47.17 | 0.0014 |
| 11 | 14 | 6 | 92.40 | 0.423 | 0.61 | 1.78 | 1.71 | 47.1 | 46.85 | 0.0027 |
| 12 | 6 | 7 | 70.10 | 0.517 | 0.76 | 2.27 | 1.86 | 46.29 | 46.2 | 0.0012 |
| 13 | 7 | 8 | 92.90 | 0.618 | 0.76 | 1.99 | 1.86 | 46.07 | 45.9 | 0.0018 |
| 14 | 11 | 13 | 90.10 | 0.106 | 0.37 | 1.90 | 1.47 | 49.75 | 49.53 | 0.0024 |
| 15 | 13 | 15 | 88.74 | 0.196 | 0.45 | 2.20 | 1.55 | 48.8 | 48.54 | 0.0029 |
| 16 | 15 | 5 | 298.50 | 0.398 | 0.61 | 1.71 | 1.71 | 48.38 | 47.67 | 0.0024 |
| 17 | 16 | 15 | 70.43 | 0.089 | 0.37 | 1.47 | 1.54 | 48.67 | 48.55 | 0.0017 |
En la Figura 9 se muestra el arreglo obtenido de la red de drenaje pluvial urbana con el método propuesto.

Figura 9 Red drenaje pluvial urbana con mínimo costo que cumple con las restricciones hidráulicas y constructivas para la precipitación con un periodo de retorno de 10 años
Para verificar que el flujo del líquido en el interior de la red es adecuado y que se cumplió con las hipótesis de funcionamiento hidráulico y las de flujo de agua en las tuberías, así como el cumplimiento con las restricciones hidráulicas de la red de drenaje, se simuló con flujo no permanente de la red con el modelo: EPA SWMM 5.0 de la Agencia de Protección del Medioambiente de Estados Unidos (Rossman, 2005).
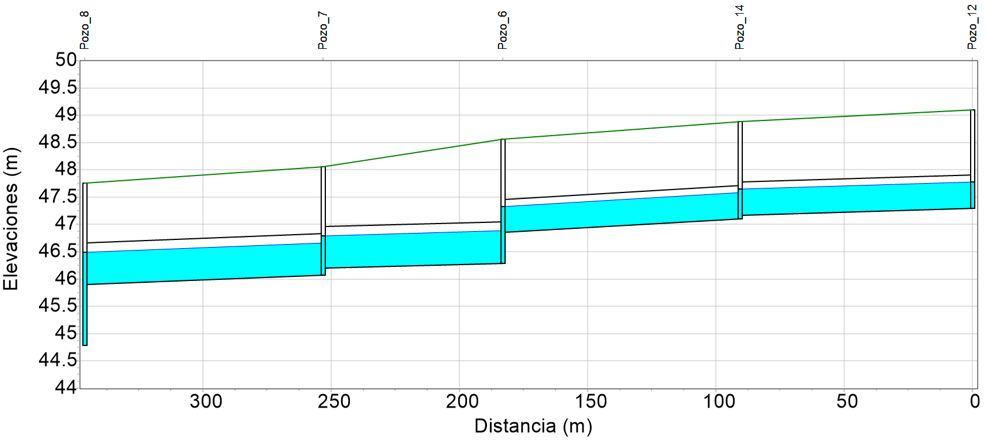
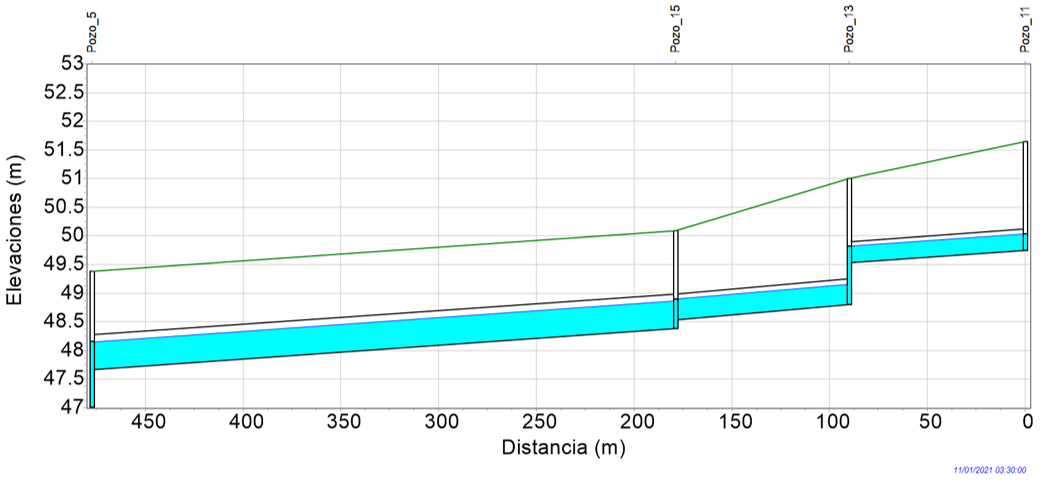
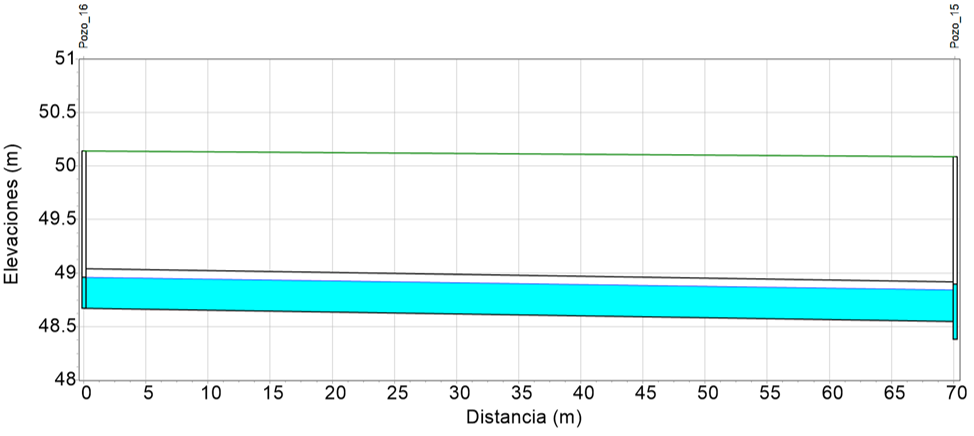
En los pozos de visita se consideraron los hidrogramas de ingreso mostrados en la Figura 6. En las Figuras 10 a 13 se muestran los perfiles de los tirantes máximos en los subcolectores apreciando que ellos se aproximaron a 80 % del diámetro, se cumplió lo que se había planteado en el método del prediseño.
En la Tabla 7 se muestran los tirantes, relación entre el tirante y el diámetro (relación de llenado) velocidades, tirante crítico y tirante normal en cada tubería obtenidos con el método matemático de flujo no permanente SWMM 5.0.
Tabla 7 Resultados de la revisión hidráulica del funcionamiento de la red de drenaje pluvial urbana resultante. Valores máximos
| Tramo | Tirante (m) | Velocidad (m/s) | Relación Y/D (%) |
Q (m3/s) |
|---|---|---|---|---|
| T1 | 0.36 | 1.07 | 80 | 0.145 |
| T2 | 0.48 | 1.5 | 79 | 0.373 |
| T3 | 0.60 | 1.43 | 79 | 0.55 |
| T4 | 0.60 | 1.87 | 79 | 0.721 |
| T5 | 0.87 | 1.6 | 81 | 1.246 |
| T6 | 0.85 | 1.83 | 79 | 1.405 |
| T7 | 0.86 | 2.13 | 80 | 1.639 |
| T8 | 0.96 | 2.39 | 79 | 2.365 |
| T9 | 1.25 | 1.62 | 82 | 2.578 |
| T10 | 0.49 | 1.23 | 80 | 0.307 |
| T11 | 0.49 | 1.69 | 80 | 0.423 |
| T12 | 0.60 | 1.35 | 79 | 0.516 |
| T13 | 0.60 | 1.61 | 79 | 0.617 |
| T14 | 0.30 | 1.15 | 80 | 0.106 |
| T15 | 0.36 | 1.44 | 80 | 0.196 |
| T16 | 0.49 | 1.59 | 80 | 0.397 |
| T17 | 0.30 | 0.96 | 80 | 0.089 |
Conclusiones
El trazo de la red de tuberías de drenaje pluvial urbano es fundamental en el proceso de diseño de una red de drenaje pluvial urbano.
Los diámetros de las tuberías que forman parte de la red de drenaje escogidas para conectar los pozos de visita, tuvieron valores de los diámetros de conductos disponibles en el comercio.
Las pendientes de las tuberías son subcríticas y la profundidad de instalación de las tuberías fue la menor posible, ya que la red diseñada corresponde a la de menor suma de los costos de adquisición de tuberías y de excavación, la cual cumplió con las restricciones hidráulicas y constructivas establecidas en manuales de redes de drenaje urbano.
La red de drenaje óptima lograda se revisó simulando matemáticamente el flujo no permanente dentro de sus conductos y utilizando el software de modelación matemática unidimensional EPA SWMM 5.0 de la Agencia de Protección del Medioambiente de Estados Unidos (Rossman, 2005).
Los resultados de la simulación de los flujos de agua en los conductos de la red de drenaje mostraron que las relaciones de llenado del flujo en las tuberías (tirante entre diámetro), eran prácticamente de 80 % (Figuras 10 a 13). Además, el caudal de flujo permanente considerado para cada tubería en el método de prediseño, no excedió al gasto máximo de la simulación matemática de las corrientes de agua variables en el tiempo que se presentaba en ella.
La simulación del funcionamiento hidráulico con flujo no permanente de la red mostró que era adecuado, por lo que se afirma que el proceso utilizado correspondía a uno de diseño de una red de drenaje pluvial urbano.
El ahorro entre el costo de la alternativa inicial considerada y la última obtenida fue de 32 %, lo cual muestra que durante el método propuesto se obtenían prediseños de redes de drenaje pluvial con menores costos.
Desde luego, la metodología es mejorable en varios de sus aspectos, como en lo referente a las pérdidas de carga en los pozos de visita y en la determinación de los hidrogramas de escurrimiento.
Es recomendable que después de diseñar este tipo de infraestructura, se realice la revisión del funcionamiento hidráulico con flujo no permanente para asegurarse que es adecuado y que se cumplen las restricciones hidráulicas de operación en cada uno de sus conductos.
La red de alcantarillado obtenida cuenta con 17 tuberías, 10 diámetros comerciales disponibles y 10 posibles pendientes por cada tramo. Para el diseño de la red se tiene un total de 1017 combinaciones de soluciones y como se aplicó varias veces el algoritmo genético llegando a resultados similares, es muy probable que se haya encontrado una solución cercana a la óptima.











 nueva página del texto (beta)
nueva página del texto (beta)