Introducción al diagnóstico del conducto de flujo
Existen muchos aspectos de mantenimiento de turbinas de gas que son afectados por las fallas y el deterioro (Boyce, 2002; Soares, 2007; Giampaolo, 1997). Algunos de estos son la confiabilidad y la seguridad de los motores, así como los costos de operación. Gracias a los sistemas de monitoreo que se han efectuado se han logrado reducir considerablemente las afectaciones a las turbinas. Estos sistemas incluyen diferentes técnicas como la termografía, el análisis de la acústica y de las vibraciones, así como el diagnóstico de conducto de flujo.
El diagnóstico del conducto de flujo permite observar el estado de salud de los componentes que integran a las turbinas de gas. En este análisis se puede considerar que son el deterioro o degradación y las averías incipientes lo que puede dañar al motor. No obstante, además de estos defectos, también pueden detectarse e identificarse anomalías en los sistemas de medición y control. Igualmente, el diagnóstico permite estimar los rendimientos principales del motor que no se miden, como la potencia del eje, el empuje, la eficiencia general del motor, el consumo de combustible específico y el margen de estabilidad del compresor.
Como cualquier tipo de diagnóstico técnico, el diagnóstico del conducto de flujo se puede dividir en tres etapas generales, que a su vez, se encuentran relacionadas entre sí (Rao, 1996). La primera es la supervisión de la salud del motor, que se refiere a la detección de la falla. La segunda, se refiere a la identificación de la falla, que implica un diagnóstico detallado. Por último, la tercera etapa consiste en la predicción del tiempo restante de la vida útil del motor. Los métodos de diagnóstico de turbinas de gas también se pueden clasificar según la dedicación a las etapas mencionadas.
Además de las etapas generales, estos métodos se dividen en dos enfoques generales (Amare et al., 2019; Jardine, 2006; Butler, 2006 y Volponi et al., 2003). El primer enfoque emplea técnicas de identificación del sistema y usa modelos basados en la física, además de requerir un completo y detallado conocimiento del sistema (Mikael, 2019). En nuestro caso, el sistema es la turbina de gas y el enfoque se llama análisis del conducto de flujo conocido en inglés como: "gas path analysis" (Volponi, 2014). Los modelos usados en este enfoque relacionan variables del conducto de flujo monitoreadas con parámetros de fallas especiales que permiten simular la degradación de los componentes del motor.
En el área de diagnóstico, el objetivo de la identificación de turbinas de gas es encontrar los parámetros de falla que minimizan la diferencia entre las variables generadas por el modelo y las medidas (Stamatis et al., 1990). Normalmente, estos modelos son complejos y requieren una cantidad significativa de recursos computacionales. El segundo enfoque (Ogaji, 2003 y Ganguli, 2013) se basa en la teoría del reconocimiento de patrones y utiliza principalmente modelos basados en datos y diferentes técnicas del reconocimiento, como redes neuronales, lógica difusa o máquinas de soporte vectorial. En estos modelos se puede obtener una relación de variables de entrada y salida de los datos reales disponibles sin la necesidad de conocer la teoría respecto al sistema analizado. La clasificación necesaria de las fallas se compone de las desviaciones en las mediciones causadas por diferentes fallas.
Ahora bien, el primer enfoque determina los parámetros de falla capaces de simular el deterioro, como se mencionó anteriormente. Es por ello que este enfoque sirve para tomar decisiones en el espacio de diagnóstico de los parámetros de falla. En el segundo enfoque, se realiza la clasificación usando las desviaciones de variables monitoreadas, por este motivo las decisiones tomadas estan en el espacio de diagnóstico de variables monitoreadas. Así, cada enfoque opera en su propio espacio diagnóstico.
La confiabilidad de las decisiones finales sobre las fallas se define por la matriz de confusión ("confusion matrix") que incluye las probabilidades del reconocimiento correcto e incorrecto de fallas de todas las clases. Varios criterios de la eficiencia de los algoritmos de diagnóstico se construyen basandose en esta matriz (Craig, 2008). Usualmente estos criterios se usan cuando se comparan los algoritmos del segundo enfoque o de diferentes enfoques (Donald, 2010; Steven & Butler, 2006). Dentro del primer enfoque, el mejor algoritmo todavía se determina por la exctitud de estimación de los parámetros de falla (Kamboukos & Mathioudakis, 2005) que no es un criterio de la eficiencia terminal de diagnóstico.
En adición al reconocimiento correcto de las fallas, la estimación de la severidad de la falla encontrada es también una función importante del diagnóstico. Esta severidad se refiere a la gravedad de los problemas causados por la falla en los componentes del motor diagnosticado. En los algoritmos que pertenecen al primer enfoque, valores absolutos de los parametros de falla se interpretan como severidades (Kamboukos & Mathioudakis, 2005). Sin embargo, si alguna clase de falla se describe por varios parametros, una medida de acción total de estos parámetros (medidada de severidad) es necesaria, pero prácticamente no se usa. Tampoco se emplea en los algoritmos del segundo enfoque (Donald et al., 2013 y Steven & Butler, 2006). Así, la severidad de fallas se determina raramente y no hay estudios dedicados al problema de la exactitud de la estimación de severidad.
En cambio, el principal objetivo de este estudio es realizar una comparación de los algoritmos en la estimación de severidad de fallas usando la exactitud de la estimación como criterio. Tal comparación de diferentes tecnicas estimadoras de severidad presenta una novedad. Este estudio contribuye a completar la comparación de los dos enfoques del diagnóstico del conducto de flujo previamente realizada en Loboda et al. (2019), ya que ahí no se consideraba todavía la estimación de la severidad de fallas.
Metodología de la comparación de tecnicas estimadoras de severidad
Fundamentos del diagnóstico de turbinas de gas
Aunque algunos estudios de fallas reales existen (Cruz, 2018), son trabajos raros y no determinan la severidad de fallas. Por lo tanto, con el fin de llevar a la práctica una buena comparación de dos algoritmos para la estimación de severidad de fallas, se creó un conjunto de datos simulados. Para esto, se ocupó el software GasTurb. Este programa ha sido desarrollado desde el inicio de los 90's por Joachim Kurzke, especialista en el rendimiento de turbinas de gas que ha trabajado desde 1970 en el área de su simulación. GasTurb presenta software profesional para cálculos de rendimiento de turbinas de gas. Es diseñado para ingenieros, gerentes e investigadores. Se utiliza en todo el mundo en una serie de industrias, así como en ciencia y educación (Gasturb, 2021). Este software ofrece una simulación no lineal basada en física para los tipos más comunes de turbinas. Se describe por la ecuación:
Donde
El vector de parámetros de falla introduce pequeños cambios en los mapas de los componentes para que de esta forma se tome en consideración una condición actual de cada componente. Los desplazamientos del comportamiento provocados por los parámetros de falla se observan en la Figura 1.
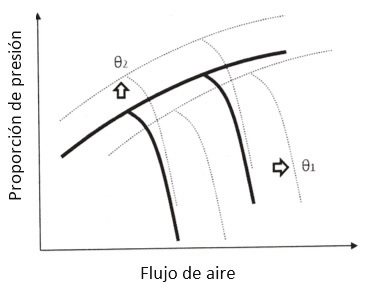
Figura 1 Diagrama del desplazamiento del comportamiento del mapa del compresor provocado por el deterioro
En este trabajo se simularon las fallas con un modelo lineal (Loboda, 2010). Este modelo se describe por la siguiente ecuación:
donde
En donde i corresponde al número de una variable monitoreada y j al número de un parámetro de falla. La variación
Para tener una simulación realista, errores aleatorios
Para simplificar el diagnóstico, las desviaciones relativas se transforman a las normalizadas según la ecuación:
Donde
Clasificación de fallas
Para reconocer fallas numerosas en un motor, estas se agrupan en clases. La clasificación total está compuesta por un número relativamente pequeño q de clases D1, D2, D3….Dq, las cuales representan posibles fallas típicas en el motor. Cada clase incluye las averías que tienen lugar en uno o más componentes del motor y tienen una gravedad variable. La clase se determina cambiando un parámetro de falla (clase de falla singular) o variando de forma independiente algunos parámetros de falla (clase de fallas múltiple).
Adicionalmente se toma una clase sana. La clase sana está compuesta por los patrones de las demás clases que se encuentren dentro de los límites de un motor saludable. Esto se hace para ejemplificar el comportamiento de los motores sin falla.
En la Figura 2 se muestran las clases de falla D1, D2 y D3 dentro del espacio de diagnóstico
Severidad de fallas
El propósito de este trabajo es comparar los dos algoritmos con el criterio de la exactitud en la estimación de severidad de fallas. Para obtener la severidad relativa de falla
Ya que en este estudio se formaron clasificaciones con diferentes tipos de clases, la severidad exacta para clases singulares se especifica por:
Para clases con dos parámetros de falla se calculó por:
Para clases con más de dos parámetros de falla se usa como valor máximo el limite
Estimación de severidad de fallas
En esta sección se presentan cuatro pasos del procedimiento de estimación de severidad de fallas por los algoritmos de enfoques diferentes. El procedimiento se desarrolló en el ambiente de Matlab.
Paso 1
Para determinar y probar los algoritmos estimadores de severidad, así como estimar sus errores en promedio, se simulan grandes cantidades de fallas de todas las clases de la clasificación aceptada. Con este motivo se generan aleatoriamente los vectores
Paso 2
Una vez que la muestra de prueba fue creada se usa la matriz inversa en estimar los parámetros de falla para el enfoque uno, según la expresión:
Esta matriz se aplica cuando el número de variables monitoreadas es igual al número de parámetros de falla. En el caso de exceso de variables monitoreadas se aplica el método de mínimos cuadrados que resulta en:
Con los parámetros encontrados
Cuando las clases de fallas se construyan por más de dos parámetros
Para resolver este problema se propone utilizar el perceptrón, también en el espacio
Paso 3
Dentro del enfoque dos que se opera en el espacio
Paso 4
El último paso de este proceso es la comparación de la exactitud de los algoritmos estimadores de severidad. La comparación se efectúa usando el error de estimación de la severidad definido por la ecuación (13). Primero se analizan y se comparan las gráficas de errores construidas contra el número de patrones para ambos enfoques. Estas gráficas se comparan para cada clase de la clasificación utilizada. Después se comparan para cada clase los errores medios cuadráticos. La comparación descrita ayudará a concluir cuál de los dos enfoques asegura mayor exactitud de la estimación de severidad de fallas.
Resultados
Condiciones de cálculos
Para realizar la metodología descrita se ha utilizado un motor de tipo turbo eje, que se puede observar en la Figura 3 publicada en Loboda et al. (2019), el cual lleva tres componentes principales: un compresor axial, una turbina de alta presión y una turbina de potencia.
En las siguientes tablas se pueden observar las mediciones escogidas. En la Tabla 1 se especifican las condiciones ambientales y de operación, donde la velocidad de rotación del compresor es la principal variable controlada. En la Tabla 2 se muestran las variables monitoreadas escogidas para este trabajo.
Tabla 1 Condiciones ambientales y de operación
| Núm. | Descripción | Sim |
| 1 | Presión ambiental | PH |
| 2 | Temperatura de entrada | TH |
| 3 | Velocidad de rotación de la turbina de potencia | npt |
| 4 | Velocidad del eje del generador de gas | nGG |
Tabla 2 Variables monitoreadas
| Núm. | Descripción | Sim |
|
| 1 | Presión del compresor | PC | 0.0050 |
| 2 | Presión de la turbina del compresor | PCt | 0.0050 |
| 3 | Temperatura del compresor | TC | 0.0084 |
| 4 | Temperatura de la turbina del compresor | TCt | 0.0049 |
| 5 | Temperatura de la turbina de potencia | Tpt | 0.0067 |
| 6 | Flujo de masa del combustible | Gf | 0.0067 |
En la Tabla 3 se observan los parámetros de falla, los cuales representan correcciones a la eficiencia y la capacidad de flujo de cada uno de los componentes del motor.
Tabla 3 Parámetros de falla
| Núm. | Descripción | Sim |
| 1 | Capacidad del compresor | δGC |
| 2 | Eficiencia del compresor | δηC |
| 3 | Capacidad de la turbina de alta presión | δAhpt |
| 4 | Eficiencia de la turbina de alta presión | δηhpt |
| 5 | Capacidad de la turbina de potencia | δApt |
| 6 | Eficiencia de la turbina de potencia | δηpt |
Los cálculos comparativos se realizaron para tres diferentes clasificaciones especificadas en la Tabla 4. A cada clasificación le corresponden sus propias muestras de entrenamiento y validación. En la Tabla 5 se muestran los parámetros de la red para cada una de las clasificaciones, estos parámetros son con los que la red trabaja de forma optimizada.
Tabla 4 Clasificaciones del estado del motor
| Clasificaciones | Clases | ||||||||||||
| D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 | D9 | D10 | D11 | D12 | D13 | |
| GC | ηC | Ahpt | ηhpt | Apt | ηpt |
GC ηC |
Ahpt ηhpt |
Apt ηpt |
GC ηC Ahpt ηhpt |
GC ηC Apt ηpt |
Ahpt ηhpt Apt ηpt |
Clase Sana |
|
| 1 | X | X | X | X | X | X | |||||||
| 2 | X | X | X | X | X | X | X | X | X | ||||
| 3 | X | X | X | X | X | X | X | X | X | X | X | X | X |
Clasificación 1
Esta clasificación está compuesta por seis clases singulares. Para la estimación en el espacio de parámetros de falla, debido a que solo se usan clases con falla simple, se tomó el resultado de la ecuación (7) como el valor estimado de severidad. En el espacio de variables monitoreadas se usó la RNA con los parámetros de la Tabla 5.
En las Figuras 4, 5 y 6 se muestran las estimaciones de severidad en ambos espacios y la severidad actual. En la Figura 4 se observa cómo los dos enfoques tratan de acercarse a la severidad actual. Se puede ver que ambas estimaciones repiten en general el comportamiento de la severidad actual (exacta). Sin embargo, la estimación de espacio
En las Figuras 5 y 6, se puede observar el comportamiento de todas las estimaciones de severidad para los espacios
La Tabla 6 muestra el error promedio del enfoque uno. Las filas muestran las clases actuales a las que pertenecen los patrones analizados y las columnas son la representación de las clases de estimación de la severidad. Podemos ver que todos los errores promedio son bastante altos y son independientes de la clase actual, pero se mantienen en el mismo nivel según su clase de estimación.
Tabla 6 Errores promedio del espacio de parámetros de falla
| Clases simuladas | Clases estimadas | |||||
| D1 | D2 | D3 | D4 | D5 | D6 | |
| D1 | 0.2085 | 0.2173 | 0.2119 | 0.2202 | 0.2182 | 0.2070 |
| D2 | 0.3020 | 0.2954 | 0.2885 | 0.2866 | 0.2921 | 0.3057 |
| D3 | 0.2228 | 0.2258 | 0.2226 | 0.2293 | 0.2300 | 0.2213 |
| D4 | 0.2483 | 0.2546 | 0.2432 | 0.2462 | 0.2457 | 0.2556 |
| D5 | 0.1968 | 0.1961 | 0.2029 | 0.2051 | 0.2019 | 0.1928 |
| D6 | 0.4970 | 0.5158 | 0.4945 | 0.5102 | 0.5270 | 0.5003 |
La Tabla 7 muestra los errores promedio del enfoque dos. Podemos ver que cada valor de la diagonal es, en general, mayor que otros elementos de la fila. Es decir, los errores de estimación de la severidad de la clase actual de fallas son más grandes que los errores de las demás clases.
Tabla 7 Errores promedio del espacio de variables monitoreadas
| Clases simuladas | Clases estimadas | |||||
| D1 | D2 | D3 | D4 | D5 | D6 | |
| D1 | 0.0629 | 0.0068 | 0.0139 | 0.0063 | 0.0439 | 0.0785 |
| D2 | 0.0073 | 0.1454 | 0.0272 | 0.1057 | 0.0074 | 0.0834 |
| D3 | 0.0078 | 0.0116 | 0.0977 | 0.0102 | 0.0052 | 0.1271 |
| D4 | 0.0077 | 0.1440 | 0.0291 | 0.1152 | 0.0076 | 0.0771 |
| D5 | 0.0384 | 0.0068 | 0.0139 | 0.0054 | 0.0586 | 0.0704 |
| D6 | 0.0122 | 0.01239 | 0.0332 | 0.0077 | 0.0115 | 0.2706 |
Así, en esta clasificación se observó que para el espacio de parámetros de falla sus errores son altos y no depende de la clase actual, sin embargo, tienen una relación baja con la clase de estimación. Para la severidad estimada en el enfoque dos se encontró que los errores son mucho más pequeños, pero estos dependen de la clase actual. Se puede concluir que en esta clasificación el enfoque uno que opera en el espacio de variables monitoreadas es más preciso.
Clasificación 2
Esta clasificación está compuesta por seis clases singulares y tres clases con falla múltiple con dos parámetros de falla. Como se mencionó anteriormente, para la estimación de severidad en el espacio diagnóstico
La Figura 7 ejemplifica los resultados de los dos enfoques para algunos patrones de la clase 7. Podemos ver que las severidades estimadas en los dos espacios generalmente se aproximan a la exacta, pero con errores mayores que se observaron anteriormente.
Las Figuras 8 y 9 exponen el comportamiento de las estimaciones por los enfoques uno y dos y los errores correspondientes. Se presentan las severidades exactas para los patrones de la clase 7 y para todas las nueve clases, las estimaciones y los errores. Se observa en la Figura 8 que los errores de estimación del enfoque uno son mayores para la clase actual 7 y las clases 1 y 2 formados por los mismos parámetros de falla que la clase 7. Para las demás clases los errores son prácticamente iguales. Los errores de todas las clases excepto la clase 7 son positivos debido a la ecuación (9). En la Figura 9 se puede ver que los errores del enfoque dos son más grandes para las mismas clases 1, 2 y 7, y positivos para las clases diferentes de la clase 7.
Comparando las Figuras 8 y 9, concluimos que en general el enfoque dos es más exacto.
La Tabla 8 muestra los errores promedio de la estimación del enfoque uno para esta clasificación. Esta tabla tiene las mismas características que las anteriores, en donde las filas muestran las clases actuales a las que pertenecen los patrones analizados y las columnas son la representación de las clases de estimación de la severidad. Podemos ver que los errores promedio son altos y dependientes de la clase actual, pero se mantienen en el mismo nivel según su clase de estimación. Además, en las clases 7, 8 y 9 el error promedio más alto se encuentra en los parámetros de falla simple que completan a la clase con falla múltiple.
Tabla 8 Errores promedio del espacio de diagnóstico de parámetros de falla para la clasificación 2
| Clases simuladas | Clases estimadas | ||||||||
| D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 | D9 | |
| D1 | 0.2106 | 0.2000 | 0.2083 | 0.2207 | 0.2154 | 0.2119 | 0.6034 | 0.5699 | 0.6514 |
| D2 | 0.2742 | 0.2863 | 0.2772 | 0.2944 | 0.2841 | 0.2828 | 0.6034 | 0.5699 | 0.6514 |
| D3 | 0.2283 | 0.2195 | 0.2210 | 0.2370 | 0.2249 | 0.2316 | 0.6034 | 0.5699 | 0.6514 |
| D4 | 0.2323 | 0.2442 | 0.2323 | 0.2467 | 0.2431 | 0.2406 | 0.6034 | 0.5699 | 0.6514 |
| D5 | 0.1974 | 0.1872 | 0.2051 | 0.2066 | 0.2072 | 0.1994 | 0.6034 | 0.5699 | 0.6514 |
| D6 | 0.4897 | 0.5207 | 0.5010 | 0.4932 | 0.4991 | 0.5127 | 0.6034 | 0.5699 | 0.6514 |
| D7 | 0.4875 | 0.4800 | 0.2452 | 0.2602 | 0.2521 | 0.2499 | 0.1622 | 0.1744 | 0.1872 |
| D8 | 0.2303 | 0.2322 | 0.4619 | 0.4712 | 0.2342 | 0.2361 | 0.2030 | 0.1251 | 0.1121 |
| D9 | 0.3734 | 0.3912 | 0.3828 | 0.3781 | 0.5601 | 0.5643 | 0.2343 | 0.3196 | 0.2457 |
La Tabla 9 en el mismo formato que la tabla previa muestra los errores promedio del enfoque dos. Podemos ver que el comportamiento de la clasificación anterior se mantiene, dentro de cada fila el valor de la diagonal de la matriz es, en general, mayor que otros elementos de la fila. Es decir, los errores de estimación de la severidad de la clase actual de fallas son más grandes que los errores de las demás clases. En comparación con la clasificación anterior, se puede ver que la misma diagonal mencionada, sube su nivel de error.
Tabla 9 Errores promedio del espacio de diagnóstico de variables monitoreadas para la clasificación 2
| Clases simuladas | Clases estimadas | ||||||||
| D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 | D9 | |
| D1 | 0.1160 | 0.0119 | 0.0152 | 0.0095 | 0.0405 | 0.0691 | 0.0779 | 0.0090 | 0.0565 |
| D2 | 0.0103 | 0.1929 | 0.0271 | 0.0908 | 0.0095 | 0.0671 | 0.0832 | 0.0218 | 0.0128 |
| D3 | 0.0136 | 0.0166 | 0.1362 | 0.0128 | 0.0095 | 0.1019 | 0.0257 | 0.0483 | 0.0162 |
| D4 | 0.0069 | 0.1186 | 0.0262 | 0.2051 | 0.0067 | 0.0652 | 0.0420 | 0.1156 | 0.0100 |
| D5 | 0.0387 | 0.0086 | 0.0114 | 0.0090 | 0.2516 | 0.0707 | 0.0138 | 0.0082 | 0.2223 |
| D6 | 0.0138 | 0.0160 | 0.0367 | 0.0097 | 0.0125 | 0.2981 | 0.0205 | 0.0107 | 0.0499 |
| D7 | 0.1789 | 0.1461 | 0.0404 | 0.0394 | 0.0188 | 0.0773 | 0.2117 | 0.0272 | 0.0313 |
| D8 | 0.0067 | 0.0535 | 0.1394 | 0.1856 | 0.0071 | 0.0258 | 0.0378 | 0.1785 | 0.0070 |
| D9 | 0.0409 | 0.0086 | 0.0105 | 0.0093 | 0.2617 | 0.1038 | 0.0184 | 0.0088 | 0.2791 |
Los resultados que se obtuvieron para esta clasificación son un poco distintos a los de la anterior. La mayor diferencia se encuentra en el espacio de parámetros de falla; los resultados muestran que los errores de las clases actuales 7, 8 y 9 tienen una relación con las clases de estimación formadas por los mismos parámetros de falla. Por ejemplo, la clase 7 que se muestra en la Figura 8 se construye por dos parámetros de falla y los errores de esta clase tienen correlación con las clases 1 y 2 formadas por los mismos parámetros de falla. En el espacio de variables monitoreadas se observó que el comportamiento es el mismo, los errores dependen de la clase a la que pertenecen. En general se puede observar que los errores siguen siendo mayores en el espacio de parámetros de falla.
Clasificación 3
Está clasificación está compuesta por seis clases con falla simple, tres clases con falla múltiple con dos parámetros de falla, tres clases de falla múltiple con cuatro parámetros y una clase de motor sano.
Como se mencionó anteriormente, cuando las clases de fallas se construyan por más de dos parámetros
En la Figura 10 se puede observar cómo las severidades estimadas de ambos enfoques se intentan aproximar a la severidad exacta para la clase 10. Esta figura presenta algunos patrones de la clase 10 que es la primera clase con falla múltiple con 4 parámetros de falla. Aquí se observa bien que el margen de error de ambos enfoques es mayor que para las clasificaciones previas.
Las Figuras 11 y 12 ilustran todos los patrones de la clase 10 presentando los valores exactos de la severidad y las estimaciones por el enfoque uno y enfoque dos para las 12 clases. Como antes, los errores de estimación en la Figura 11 (enfoque uno) dependen de la clase actual. Sin embargo, a diferencia con las clasificaciones anteriores, los errores del enfoque uno ahora aumentaron. Esto se debe a dos situaciones: La primera es que la adición de 4 clases nuevas inclusive una clase de motor sin fallas aumentó la complejidad del reconocimiento de las fallas. La segunda se debe al cambio de técnica en la estimación de la severidad en el espacio de parámetros de falla. En la Figura 12, podemos ver los errores de la estimación del enfoque dos. A diferencia de las clasificaciones anteriores, el nivel de errores es mayor. Este nivel ahora es cercano al nivel de errores del enfoque uno (Figura 11). Además, el comportamiento de las estimaciones de severidad por ambos enfoques parece similar, que se explica por la misma red neuronal artificial usada.
La Tabla 10 muestra los errores promedio que se obtuvieron del enfoque uno (espacio de los parámetros de falla). Podemos ver que el comportamiento de los errores promedio es diferente a las clasificaciones anteriores. Dentro de cada fila el valor de la diagonal de la matriz presentada es, en general, mayor que otros elementos de la fila. Es decir, los errores de estimación de la severidad de la clase actual son más grandes que los errores de las demás clases.
Tabla 10 Errores promedio del espacio de diagnóstico de enfoque uno para la clasificación 3
| Clases simuladas | Clases estimadas | ||||||||||||
| D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 | D9 | D10 | D11 | D12 | D13 | |
| D1 | 0.1821 | 0.0115 | 0.0220 | 0.0106 | 0.0386 | 0.0151 | 0.0316 | 0.0156 | 0.0794 | 0.0169 | 0.0870 | 0.0530 | 0.0374 |
| D2 | 0.0161 | 0.2364 | 0.0206 | 0.1054 | 0.0130 | 0.0159 | 0.1366 | 0.0634 | 0.0226 | 0.0425 | 0.0383 | 0.0371 | 0.0436 |
| D3 | 0.0201 | 0.0189 | 0.2284 | 0.0167 | 0.0131 | 0.0162 | 0.0501 | 0.0680 | 0.0254 | 0.0262 | 0.0170 | 0.0614 | 0.0608 |
| D4 | 0.0149 | 0.1277 | 0.0241 | 0.2181 | 0.0091 | 0.0171 | 0.0653 | 0.1950 | 0.0186 | 0.0505 | 0.0224 | 0.0626 | 0.0325 |
| D5 | 0.0482 | 0.0175 | 0.0181 | 0.0168 | 0.2587 | 0.0185 | 0.0188 | 0.0139 | 0.3181 | 0.0166 | 0.0411 | 0.0462 | 0.0387 |
| D6 | 0.0291 | 0.0118 | 0.0206 | 0.0182 | 0.0278 | 0.7443 | 0.0257 | 0.0211 | 0.0815 | 0.0141 | 0.0426 | 0.0552 | 0.3256 |
| D7 | 0.1376 | 0.1559 | 0.0219 | 0.0371 | 0.0152 | 0.0143 | 0.3822 | 0.0421 | 0.0283 | 0.0682 | 0.1435 | 0.0769 | 0.0390 |
| D8 | 0.0154 | 0.0506 | 0.1697 | 0.2045 | 0.0078 | 0.0111 | 0.0497 | 0.4048 | 0.0160 | 0.0844 | 0.0206 | 0.0739 | 0.0306 |
| D9 | 0.0427 | 0.0123 | 0.0161 | 0.0166 | 0.2367 | 0.0593 | 0.0222 | 0.0156 | 0.4642 | 0.0144 | 0.0717 | 0.0655 | 0.0709 |
| D10 | 0.0325 | 0.0842 | 0.0668 | 0.0861 | 0.0126 | 0.0127 | 0.1049 | 0.1451 | 0.0198 | 0.2935 | 0.0409 | 0.0936 | 0.0314 |
| D11 | 0.1361 | 0.0415 | 0.0225 | 0.0258 | 0.0550 | 0.0209 | 0.1321 | 0.0262 | 0.1398 | 0.0327 | 0.4025 | 0.1095 | 0.0417 |
| D12 | 0.0400 | 0.0305 | 0.0850 | 0.0474 | 0.0475 | 0.0241 | 0.0837 | 0.0998 | 0.1103 | 0.0831 | 0.1389 | 0.2972 | 0.0466 |
| D13 | 0.0230 | 0.0206 | 0.0508 | 0.0233 | 0.0275 | 0.1080 | 0.0363 | 0.0240 | 0.0514 | 0.0111 | 0.0221 | 0.0279 | 0.3413 |
La Tabla 11 muestra los errores promedio que se obtuvieron del enfoque dos. Podemos ver que se mantiene el comportamiento observado para las clasificaciones anteriores: dentro de cada fila el valor de la diagonal de la matriz es, en general, mayor que otros elementos de la fila. Es decir, los errores de estimación de la severidad de la clase actual son más grandes que los errores de las demás clases. En comparación con las clasificaciones anteriores, se puede ver que el nivel de errores del enfoque dos aumentó. Comparando las Tablas 9 y 10, podemos concluir que en general los errores del enfoque uno ahora igualan a los del enfoque dos. El mejoramiento del enfoque uno se explica por el uso de la red neuronal artificial en este enfoque aplicado para la clasificación 3.
Tabla 11 Errores promedio del espacio de diagnóstico de enfoque dos para la clasificación 3
| Clases simuladas | Clases estimadas | ||||||||||||
| D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 | D9 | D10 | D11 | D12 | D13 | |
| D1 | 0.1933 | 0.0185 | 0.0202 | 0.0133 | 0.0412 | 0.0163 | 0.0370 | 0.0190 | 0.0730 | 0.0172 | 0.0910 | 0.0530 | 0.0298 |
| D2 | 0.0142 | 0.2381 | 0.0284 | 0.1016 | 0.0138 | 0.0253 | 0.1308 | 0.0625 | 0.0205 | 0.0449 | 0.0405 | 0.0423 | 0.0303 |
| D3 | 0.0172 | 0.0212 | 0.2119 | 0.0150 | 0.0119 | 0.0148 | 0.0442 | 0.0555 | 0.0242 | 0.0256 | 0.0206 | 0.0539 | 0.0635 |
| D4 | 0.0132 | 0.1306 | 0.0227 | 0.2235 | 0.0118 | 0.0272 | 0.0649 | 0.1925 | 0.0197 | 0.0564 | 0.0211 | 0.0596 | 0.0219 |
| D5 | 0.0426 | 0.0209 | 0.0202 | 0.0142 | 0.2618 | 0.0174 | 0.0216 | 0.0193 | 0.3156 | 0.0150 | 0.0492 | 0.0403 | 0.0314 |
| D6 | 0.0201 | 0.0238 | 0.0290 | 0.0201 | 0.0136 | 0.7353 | 0.0306 | 0.0244 | 0.0647 | 0.0177 | 0.0348 | 0.0504 | 0.3481 |
| D7 | 0.1379 | 0.1537 | 0.0246 | 0.0411 | 0.0144 | 0.0194 | 0.3825 | 0.0380 | 0.0314 | 0.0722 | 0.1415 | 0.0833 | 0.0375 |
| D8 | 0.0116 | 0.0535 | 0.1564 | 0.2024 | 0.0100 | 0.0203 | 0.0499 | 0.4009 | 0.0227 | 0.0821 | 0.0199 | 0.0739 | 0.0249 |
| D9 | 0.0379 | 0.0182 | 0.0148 | 0.0149 | 0.2328 | 0.0458 | 0.0208 | 0.0178 | 0.4628 | 0.0148 | 0.0704 | 0.0549 | 0.0668 |
| D10 | 0.0296 | 0.0777 | 0.0635 | 0.0754 | 0.0110 | 0.0222 | 0.1087 | 0.1491 | 0.0247 | 0.289 | 0.0434 | 0.0889 | 0.0260 |
| D11 | 0.1328 | 0.0449 | 0.0271 | 0.0253 | 0.0517 | 0.0254 | 0.1280 | 0.0233 | 0.1413 | 0.0306 | 0.4059 | 0.1139 | 0.0428 |
| D12 | 0.0367 | 0.0312 | 0.0811 | 0.0441 | 0.0493 | 0.0293 | 0.0813 | 0.1016 | 0.1118 | 0.0826 | 0.1470 | 0.2971 | 0.0492 |
| D13 | 0.0220 | 0.0261 | 0.0563 | 0.0203 | 0.0232 | 0.0994 | 0.0372 | 0.0269 | 0.0559 | 0.0144 | 0.0191 | 0.0299 | 0.3386 |
Comparando las Tablas 6, 8 y 10 que corresponden al enfoque uno, podemos concluir que el aumento del número de clases causa un incremento de errores de la estimación de severidad. La misma conclusión sigue de la comparación de las Tablas 7, 9 y 11 del enfoque dos. Esta tendencia mencionada es natural y se explica por aumento del número de parámetros que estimamos con el mismo volumen de datos de entrada. Lo mismo siempre sucede con las probabilidades de reconocimiento de fallas, sus errores crecen cuando incrementa el número de fallas consideradas.
Conclusiones
En este trabajo se estudió un problema todavía poco investigado, el problema de la estimación de severidad de fallas de turbinas de gas. Aunque hay algunos estudios de la severidad, no se encuentran trabajos completamente dedicados a este problema. En el área del diagnóstico de turbinas de gas se mantienen dos enfoques principales: enfoque uno, que opera en el espacio de parámetros de falla, y el enfoque dos, que hace diagnostico en el espacio de variables monitoreadas. Este trabajo evalúa la calidad de estimación de la severidad por los algoritmos de cada enfoque.
Con el fin de saber con certeza desde qué espacio de diagnóstico es más exacto se realizaron tres diferentes clasificaciones. Para las dos primeras, los resultados demostraron que en el espacio de variables monitoreadas se obtuvo una mejor exactitud. Por otro lado, en la tercera clasificación, en donde se usó por primera vez la técnica de redes neuronales artificiales para el enfoque uno, la exactitud de los enfoques es básicamente la misma. Así, podemos concluir que usualmente el enfoque dos tiene una mayor exactitud en la estimación de severidad de fallas, aunque la integración de la red neuronal artificial en el enfoque uno permite mejorarlo considerablemente subiendo la exactitud de este enfoque hasta la exactitud del enfoque dos.











 nueva página del texto (beta)
nueva página del texto (beta)














