1. Introduction
The maneuver studied here can be called “powered aero-gravity-assist maneuver”, because it is subjected to three different effects at the same time: (i) the rotation of the velocity of the spacecraft due to the gravity of the planet that the spacecraft is passing by (Nock & Uphoff 1979; Uphoff 1989; Dowling et al. 1991, 1992; Broucke 1988; Broucke & Prado 1993; Qi & Xu 2015; Chandra & Bhatnagar 2000; Prado 2007; Gomes & Prado 2010); (ii) the forces coming from the action of the atmosphere on the trajectory of the spacecraft, considering both drag and lift (Gomes et al. 2016) and; (iii) the modification of the orbit made by an impulsive maneuver applied to the spacecraft when it is passing by the periapsis of its orbit around the planet (Prado 1996; Casalino et al. 1999b; Silva et al. 2013a,b; Silva et al. 2015). The literature has several published researches related to those maneuvers, either considered individually or combining some of the aspects mentioned above. The combination of those three aspects has been studied for the first time recently (Piñeros & Prado 2017), considering direct orbits around the Earth. Therefore, the present paper follows the previous one and has the goal of studying two new aspects. The first one is the possibility of using retrograde orbits for this maneuver, so analyzing the differences compared to direct orbits. Retrograde orbits have larger relative velocity between the spacecraft and the atmosphere of the planet, so it is important to see in detail how much this higher velocity modifies the effects of this maneuver. The second aspect is to verify the applicability of this type of maneuver to the planet Mars, because it is in a very strategic place to reach other planets of the Solar System. Besides that, it is a planet that deserves to be studied in detail, so missions passing close to it are always interesting in terms of scientific research.
The pure gravity-assist maneuver is the most studied aspect of this maneuver. It consists in making the spacecraft pass close to a celestial body to rotate its velocity vector with respect to an inertial frame, so acting like applying an impulsive maneuver on the spacecraft. This rotation can provide or remove energy from the spacecraft with respect to the primary, depending on whether the passage is in front or behind the celestial body (Broucke 1988; Broucke & Prado 1993). Real applications of this technique are very well described in papers like Flandro (1966) and Kohlhase & Penzo (1977), which made the initial planning of the Voyager missions that launched two spacecraft to explore the exterior planets of the Solar System using closeapproaches to several planets to give energy to the spacecraft. The Galilean moons of Jupiter can also provide gains or losses of energy, although not as large as Jupiter itself (Longman & Schneider 1970; Lynam et al. 2011). The Galileo mission also used this principle, and several aspects of this maneuver are shown in D’Amario et al. (1981, 1982) and Byrnes & Damario (1982). A very interesting aspect of the close approach maneuver is to make orbital plane change maneuvers, which are usually a very expensive part of the whole mission. Carvell (1986) shows this possibility, describing an application for the Ulysses mission, which used the planet Jupiter to make an orbital change of almost 90°. A sequence of swingbyes is also an option for space missions, as shown in Dunham & Davis (1984), when considering maneuvers around the Moon. Missions using the planet Venus are shown in Striepe & Braun (1989), which send a spacecraft to Venus to gain energy enough to reach Mars. The main goal of this paper is to reduce the duration of the mission to Mars, by using a gravity assist in Venus to plan the trip to Mars, arriving there close to the launch window for a Hohmann transfer back to the Earth. Venus was also used in Hollister & Prussing (1965) for similar maneuvers. Missions to Pluto using close approaches are described in Longuski & Williams (1991) and Weinstein (1992). Missions to Neptune are considered in Swenson (1992) and Solórzano et al. (2006). General mappings of trajectories around the Moon are shown in Prado & Broucke (1995a). Prado (1997) studied swing-by trajectories taking into account the eccentricity of the primaries. Felipe & Prado (1999) mapped three-dimensional swingbyes around Jupiter. Using a different approach, Strange & Longuski (2002) developed a graphical method to optimize swing-by trajectories with respect to the mass at the launch phase and/or the flight time. An Europa orbiter tour using swingbyes was designed and shown in Heaton et al. (2002).
The topic of powered swing-by maneuvers is little studied in the literature. It is a combination of a passage of a spacecraft by a celestial body with the application of an impulse. A few studies about this topic are shown in Prado (1996); Casalino et al. (1999b); Silva et al. (2013a,b); Silva et al. (2015), all of them studying maneuvers around the Moon. They show the best direction and location to apply the impulse of the maneuver, inside or outside the sphere of influence of the Moon (Araujo et al. 2008). An extension considering a cloud of particles performing a close approach is also available in the literature (Gomes et al. 2013b,a; Gomes & Prado 2008). Analytical studies are made in Prado & Felipe (2007). More complex maneuvers, combining low thrust and swingbyes, are also considered in the literature. Some examples are found in Casalino et al. (1999a); McConaghy et al. (2003); Okutsu et al. (2006); dos Santos et al. (2008).
Maneuvers passing through the atmosphere of a planet can also be found. Gomes et al. (2013a); Prado & Broucke (1995b) consider only drag. The aero-gravity assist (AGA) maneuvers considering the presence of lift can be used to increase or decrease the effects of the close approach, depending on the direction of the lift, as shown in the results of Piñeros & Prado (2017) and in the present paper.
Other studies relevant to the present research include McRonald & Randolph (1992), who considered L/D ratios up to 10 for AGAs in interplanetary trajectories, using hypersonic waveriders. They considered close approaches with the planets Mars, Venus and Earth. Trajectories to Pluto, also using high L/D ratios, are available in Johnson & Longuski (2002). One of the important aspects of the solutions with high L/D ratio is the low energy loss from drag, as shown in Sims et al. (1995, 2000), who identified that maneuvers to the outer planets can benefit from passages near Venus and/or Mars to reduce launch energy and time of flight. Algorithms to design trajectories using those planets are available in Eugene et al. (2000); Lavagna et al. (2005). The Waverider vehicle shape is designed in detail in Armellin et al. (2007), for maneuvers using the atmosphere of Mars. A study of returning trajectories using the atmospheres of Earth, Mars and Venus was done by Henning et al. (2014). A double-flyby in Mars is considered by Jesick (2015) and Mars free-return trajectories are available in Hughes et al. (2015). Gomes et al. (2016) studied AGA with the Earth, also as a function of the angle of approach, L/D ratios and ballistic coefficient. Mazzaracchio (2014) studied flight-path guidance for aero-gravityassist maneuvers.
Therefore, the goal of the present paper is to consider a more complete maneuver, including a close approach with a passage inside the atmosphere of the planet, and assuming the existence of lift and drag, combined with the application of an impulse to the spacecraft when it is passing by the periapsis of its trajectory around the planet. This aspect was first considered in Piñeros & Prado (2017), studying direct orbits around the Earth. The present paper extends this study to consider retrograde orbits and the planet Mars as the celestial body for the close approach. Retrograde orbits need to be analyzed in detail, because the relative velocity between the spacecraft and the atmosphere of the planet is larger. This may help to get more effects from the maneuver, but may also generate collisions with the planet due to the larger drag. It means that simulations need to be done for specific missions to ensure a the applicability of this type of maneuver for retrograde orbits. The use of the planet Mars is also another interesting and new aspect of the results presented here. This planet has been considered in many missions for close approaches with and without the presence of the atmosphere, since it is located in a strategic position to help a spacecraft coming from the Earth to reach the outer planets and the other way around. In particular, return trips may come in the retrograde sense, after making a close approach with the target body of the mission in the outer Solar System. Mars is also in an orbit near the Earth, so it requires small amounts of fuel and shorter trip times to be reached. It has an atmosphere large enough to affect the trajectories of a spacecraft passing through, as already cited. The mathematical model used in the present paper considers the restricted three-body problem (Szebehely 2012) with the effects of the atmosphere of Mars added, which is assumed to have a density given by an exponential model. The impulse is added as an extra velocity at the correct moment. The final goal is to obtain a maneuver that is more efficient in terms of fuel savings compared to other types of orbital maneuvers (Hohmann 1925; Marchal 1967; Smith 1959; Gomes & Prado 2011; Sukhanov & Prado 2001; Biggs 1978, 1979) using impulses or low thrust.
Retrograde orbits are studied, as well as a detailed comparison with the direct orbits, since neither of those cases were studied before for the planet Mars. The effects of the atmosphere are measured by the ballistic coefficient, which varies from zero (no atmosphere) to 5.0 × 10-7km2/kg. The lift to drag ratio (L/D) takes the values -9.0, -1.0, 0.0, 1.0 and 9.0. They are assumed to be constant during the maneuver. The situation with variable (L/D) is left for further studies. The highest values of L/D can be obtained by waveriders, as already explained. Therefore, the present research is a continuation of the research performed in Gomes et al. (2016), who studied aero-gravity-assist maneuvers including drag and lift, but did not consider the application of an impulse. The present study combines a the effects in the energy variation obtained from AGA maneuvers with Mars with those resulting from the more complete maneuver, which includes the application of an impulsive maneuver when the spacecraft passes by the periapsis of its trajectory around Mars. The dynamical model is shown in § 2, based in the Restricted Three-Body Problem (RTBP), but removing the usual limitations assumed by models like the “patched-conics”. In this way, the present research can map retrograde and direct powered aero-gravityassist trajectories around Mars. Of course this type of maneuver is not easy, and the present study has the goal of showing a potential that exists in nature, taking into account practical aspects of a mission.
2. Dynamical model
The dynamical model assumes the presence of three bodies: the largest body M1 (the Sun in the present case), a second body with mass M2 (Mars) and a third body that is assumed to have a negligible mass M3 (a space vehicle passing by Mars). The first two bodies are moving in Keplerian circular orbits around their common center of mass. M3 starts its motion around M1 and, after some time, makes a close approach with M2. The change in the trajectory of M3 around M1 due to this passage close to M2 is called fly-by or swing-by maneuver. The equations of motion used here are those of the restricted three-body problem (Szebehely 2012) with the inclusion of the terms coming from the atmosphere of Mars:
where FxAtm and FyAtm are the components of the forces coming from the atmosphere of Mars and Ω is the potential, given by:
The components of the forces coming from the atmosphere of Mars are obtained from:
where
To be more general, the mass of the spacecraft (m), its area (A) and the drag coefficient are included in only one parameter, which is called ballistic coefficient (CB) (Broucke & Prado 1993). To express the relations between lift and drag, the coefficient CBL = CB(CL/CD) is used.
The variations of energy can be measured in the inertial reference system, considering the instants before and after the passage by Mars, using equations 8 and 9 (Prado 2007), respectively.
From these equations, it is possible to obtain the variations of energy, easily calculated from the variable∆E=E++E−.
To obtain the numerical results, a periapsis altitude of 153 km is fixed in all the simulations. This value is not varied because it is just a scale factor, so keeping it fixed reduces the number of parameters to simplify our study. For the angle of approach, the two most important values are used: 90° and 270°, which are the values for the maximum energy losses and gains, respectively (Broucke 1988). Once those choices are made, a numerical backward integration is performed (Neto & Prado 1998) from the periapsis, with no influence from the atmosphere (CB = 0), until a point that can be considered to be far from Mars, such that the system Sun-spacecraft can be considered a “two-body” system. The dynamics given by the restricted three-body problem is used in this step. The state vector (position and velocity) of the spacecraft at this initial point is used as initial conditions for the next steps. This means that every time the trajectories are obtained from the numerical integrations of the equations of motion, the spacecraft starts from this point and the integrations are performed in positive times, considering the forces coming from the atmosphere of Mars. For the GA maneuvers, the natural motion takes the spacecraft close to Mars, passes outside its atmosphere and goes to another point, distant from Mars. It is then possible to calculate the variations of energy given by the GA maneuver (Prado & Broucke 1995a).
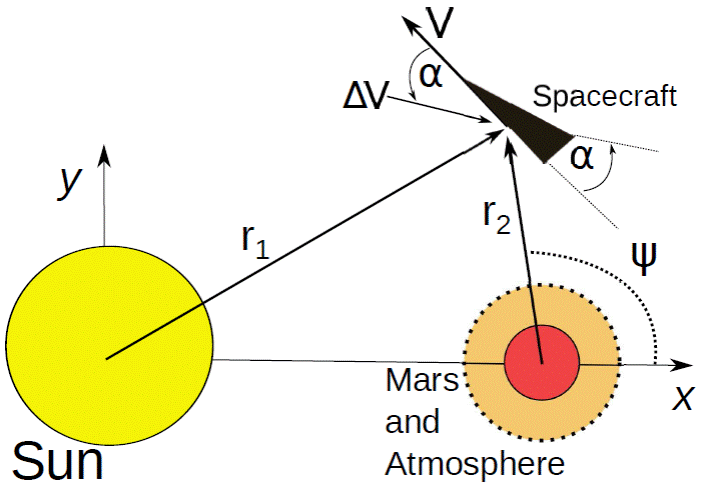
To make the more complex AGA maneuver, the spacecraft starts from the same initial state used in the previous option (GA), but this time the atmosphere is included in the dynamics. The values of the ballistic coefficient vary from 0.0 to 5.0 × 10-7km2/kg. The same strategy applied to GA maneuvers is used to obtain the variations of energy. Aerocapture, aerobraking and reentry are verified and trajectories included in this list are excluded from the results. The more complex maneuver, including the application of an impulse at the periapsis, is the goal of the present paper. It is the same maneuver explained in the previous paragraph (AGA), but with the addition of an impulse at the periapsis. Figure 1 shows the maneuver in more detail. The dynamical system has Mars in a circular orbit around the Sun. All the trajectories for the spacecraft are assumed to be in the orbital plane of the primaries. For the atmosphere of Mars, a simple exponential model4is used, given by ρ = 0.020exp(−h/11.1) kg/m3, where h is the altitude in km. The numerical integrations are made using a Runge-Kutta-Fehlberg 7/8 order integrator [68] with adaptative stepsize.
3. Results
Next, several families of results are shown, to guide the interpretation of the effects of the atmosphere of Mars in the powered aero-gravity-assist trajectories. Retrograde and direct trajectories are considered to verify the differences coming from this aspect. In all the simulations, the velocity at periapsis is fixed at 12.03 km/s (0.5 canonical units), which is a value used in previous researches which showed to give maneuvers with effects on the variations of energy which do not present too many captures or collisions. The altitude of the periapsis is fixed at 153 km. Those values were used for the same reason; presenting important variations of energy with few captures or collisions. Both of those values are fixed, because they are just scale factors. The only consequence of modifying these variables is to increase or decrease the effects of the atmosphere, as already explained, acting as a multiplicative factor in the horizontal axis. It is also important to note that this problem has too many parameters, so it is necessary to fix some of them to be able to get some conclusions. To make the results comparable with the equivalent ones coming from the Earth (Piñeros & Prado 2017), an altitude of 153 km is used here because it has the same density of the atmosphere of the Earth at 120 km, the value used in (Piñeros & Prado 2017). So, the differences in the results stem from the differences in the velocities of the decay of the two atmospheres.
For the angle of approach, the values used here are 90°, representing the maximum loss of energy; and 270°, representing the maximum gain of energy (Broucke 1988). For the ratio lift/drag (L/D), five values are used: −9, for a maneuver near the maximum lift pointing to Mars (Johnson & Longuski 2002; Lewis & McRonald 1992, 1991; Randolph & Mcronald 1992); −1, for a maneuver where drag and lift have the same magnitude and the lift points towards Mars; 0, for a maneuver with drag only (like done for the Earth in reference (Prado & Broucke 1995b); 1, for a maneuver where drag and lift have the same magnitude and the lift points opposite to Mars; 9, for a maneuver near the maximum lift pointing opposite to Mars (Johnson & Longuski 2002). For the impulsive maneuver, the values 0.0 and 0.5 km/s are used for the magnitude of the impulse, which represent an unpowered and a powered maneuver with practical values for the magnitude of the impulse, since larger impulses are hard to implement.
The results analyze the effects of the atmosphere and the direction of the impulse for maneuvers around Mars. The plots indicate the energy variation per unit mass in canonical units in color codes, with the ballistic coefficient in the horizontal axis and the direction of the impulse in the vertical axis. The magnitude of the impulse, the L/D ratio and the angle of approach of the maneuver with no atmosphere are fixed for each plot. Therefore, several plots are made to measure the effects of those variables. The range for the direction of the impulse is from −180°to 180°, covering the whole possible interval, and values of CB go from zero (no atmosphere) up to 5.0 × 10−7km2/kg. This maximum value is chosen from the literature (Gomes et al. 2016; Piñeros & Prado 2017). Figures 2 to 9 show the results. The +L/D direction is in the same direction of r2, opposite to Mars, and the −L/D direction is against the position vector r2, or in the direction of Mars. The impulse angle is 0° when the impulse acts against the velocity at the periapsis Vp and 180° when it acts in the direction of Vp. The angles increase in the clockwise sense, and decrease counterclockwise. This means that 90° is used for an impulse in the direction of the planet and −90° for the opposite direction.
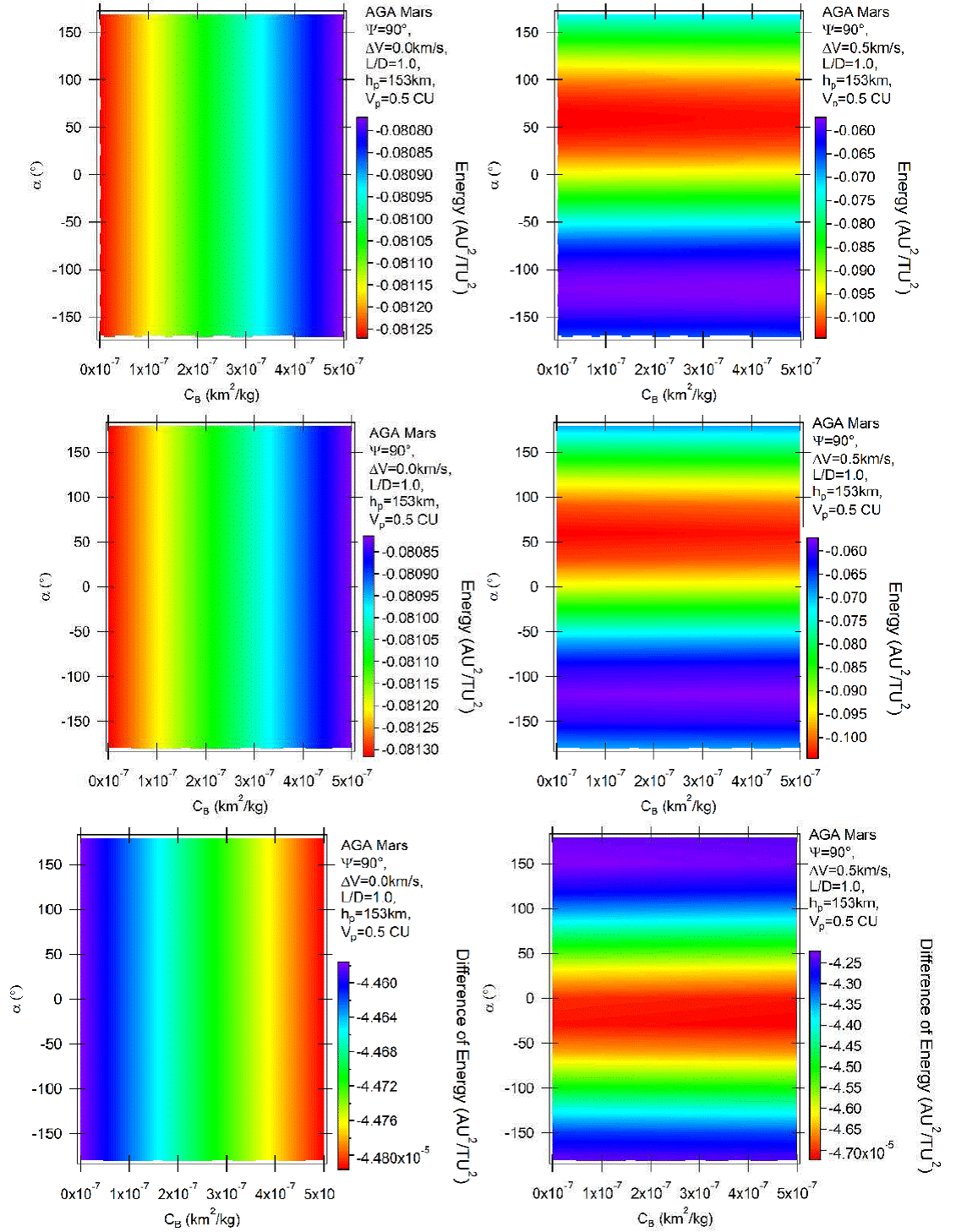
Fig. 2 Variation of energy per unit of mass as a function of the angle of attack for AGA with L/D = 1 and ψ = 90° for retrograde (above) and direct (middle) orbits. The differences between direct and retrograde orbits are shown in the bottom part of the figure. The color figure can be viewed online.
Figure 2 considers the case where L/D = 1 and ψ = 90° (a maneuver that removes energy from the spacecraft [Broucke 1988]), for both direct and retrograde orbits. The upper part of the figure represents the retrograde orbits, the main goal of the present research, while the middle parts show the results for direct orbits, since those results are not available in the literature for Mars. The bottom parts of the figure show the differences between direct and retrograde orbits, defined as “variation of energy of the direct orbit − variation of energy of the retrograde orbit”. The left side considers the unpowered maneuvers, the powered ones, using a magnitude of 0.5 km/s, are shown on the right side. Looking at the unpowered retrograde orbits (upper left plot), it is clear that the energy losses decrease with the ballistic coefficient. This means that the maneuver loses less energy when the atmosphere increases its effect. This is the net result of the extra energy removed directly by the drag when the atmosphere has a strong effect and the reduction of the energy loss due to the decrease of the angle of curvature caused by the positive lift, which sends the spacecraft in the direction opposite to Mars, so reducing the curvature of the trajectory and, consequently, the effect of the gravity part of the maneuver. There is also a small effect, removing the angle of approach from the optimal point, which helps to reduce the energy losses. The direct unpowered orbits are shown in the left-middle plot of the figure. The results are similar. The difference in the energy variation is shown in the bottom plot of the figure and it indicates differences in the order of 0.0001 AU2/TU2 (about 0.025 km2/s2), with retrograde orbits having smaller losses of energy. It is shown by the negative signs of the color scale. Retrograde orbits are the ones with higher relative velocity between the spacecraft and the atmosphere, because their motion is against the direction of the motion of Mars. This difference means that the action of the lift force in changing the angle of approach is more important than the extra removal of energy from the larger drag of the retrograde orbits. This is an interesting result from the present analyses, because a first look at the problem would suggest larger reductions of energy due to the extra relative velocity spacecraft-atmosphere. It is also shown that for the non-powered maneuver the differences decrease a little with the increase of the effects of the atmosphere.
Figure 2 also studies the powered maneuver. In this case the color scales are the same for direct and retrograde orbits, because the impulse dominates the maneuver and the differences in the variations of energy are not large enough to modify the scale. The results expressed by colors confirm the existence of retrograde orbits, with similar magnitudes in the energy variations compared to direct ones. The dependency of the differences in the variations of energy between direct and retrograde orbits on the atmosphere is very weak, with the direction of the impulse dominating the scenario. Of course the angle α plays an important role in the maneuvers. In the region where ψ is larger than about 120°, green and blue colors dominate. This indicates smaller reductions of energy. Regions between zero and 120° concentrate the larger losses of energy. The maximum losses of energy occur near α = 60°, with the impulse having a component in the direction of Mars, so increasing the effects of the atmosphere and increasing the rotation angle of the maneuver and a component opposite to the direction of the motion of the spacecraft, so removing directly energy from the spacecraft. Regions below −60° are dominated by the blue color, which indicates the minimum losses of energy. This region has applied impulses with a component in the opposite direction of the motion of the spacecraft and a component pointing in the opposite direction of Mars, leaving as net result a decrease of the effect of the gravity part of the maneuver. Comparing the results obtained here with the direct orbits in maneuvers using the Earth for the close approach showed in Pineros and Prado [17], the general behavior is similar, but the magnitude of the energy variations is different. It is important to mention that the results are in canonical units, both in the present paper and in the reference (Piñeros & Prado 2017). Energy variations are measured in units of the square of the velocity. The conversion to metric units is made using the orbital velocity of the planet around the Sun. It is 24.07 km/s for Mars and 29.78 km/s for the Earth. Therefore, the variations of energy obtained for the Earth need to be divided by the constant 0.6533 (24.07/29.78)2 to be compared with the results obtained for Mars. From Piñeros & Prado (2017) it is clear that, in the case of the Earth, the variation of energy goes from −0.0269 to −0.0275 canonical units. Dividing by the constant 0.6533, the interval would be −0.0412 to −0.0421 in the canonical system of units used for Mars. The present paper shows that the results for Mars are in the interval −0.0809 to −0.0813 canonical units, which is about twice the effect for the Earth. The reason is that the combination of the masses, sizes and distribution of density of the atmospheres of both planets makes Mars a more efficient body for this type of maneuver.
Figure 3 shows the results for L/D = 9 and ψ = 90°. Similarly to Figure 2, the upper part of the figure shows the retrograde orbits, the middle part the direct orbits and the bottom parts the differences. Studying the unpowered retrograde orbits (upper left plot), the same general behavior with energy losses decreasing with the ballistic coefficient is observed. The main difference is the much larger interval of energy variations obtained for the L/D = 9 case, in particular, in the upper part of the limit, which is now from −0.073 to −0.081 canonical units. It was from −0.0813 up to −0.0809 canonical units when L/D = 1. The reason is that the higher value of the lift moves the spacecraft away from Mars, so reducing the losses of energy by the maneuver. Therefore, a high lift increases the atmospheric effects, as explained in the case L/D = 1. The direct unpowered orbits are shown in the left-middle plot of the figure to complete the analyses, but the results are similar, with differences in the energy variation of the order of 0.0001 AU2/TU2. The bottom parts of the figure show those differences in detail. It is noted that the higher value of the lift does not impact in a significant way those differences. The powered maneuvers are also shown, in the right side of Figure 3. The results confirm the existence of retrograde and direct orbits using Mars as the body for the close approach, with similar magnitudes. The angle α plays the same important role described in the case L/D = 1. The maximum losses of energy occur near α = 60°, where the impulse has components in the direction of Mars and opposite to the direction of the motion of the spacecraft. Regions below −60°, where the impulses have components against the direction of the motion of the spacecraft and components pointing in the opposite direction of Mars, get smaller effects from the maneuver. Looking at the results obtained in Piñeros & Prado (2017) for the Earth, the general behavior is similar, but the magnitudes of the energy variations are different. A first observation is that using the Earth it is possible to obtain zero variations of energy in some cases, which does not occur for Mars. This type of maneuver can be used to make closer observations of the planet without modifying the energy of the trajectory, if required by the mission. The interval for the Earth after the corrections made for the different metric units of both systems goes from 0.00 to −0.06 canonical units, while for Mars it is from −0.05 to −0.10 canonical units. Note that Mars can cause larger losses of energy, almost twice the results obtained in the previous case. Another point to be observed is the increase of the effects from the atmosphere. This is shown by the inclinations of the border lines between two adjacent colors. Note the yellow lines separating green and red colors. Those lines were very close to horizontal in the case of L/D = 1, and now they are strongly inclined. For a fixed horizontal (α constant), it is clear that the increase of the ballistic coefficient reduces the losses of energy. The reason is that the positive lift decreases the effect of the gravity part of the maneuver. This means that the high value for the lift adds a dependency on the ballistic coefficient, due to the more active participation of the atmosphere in the total maneuver. These results are hard to predict in advance, since they depend on several factors listed before (masses, sizes and distribution of density of the atmospheres of both planets) and also on the magnitude of the impulse applied, which competes with the gravity of the planet. Those are the reasons why only the numerical simulations made here are able to provide results.
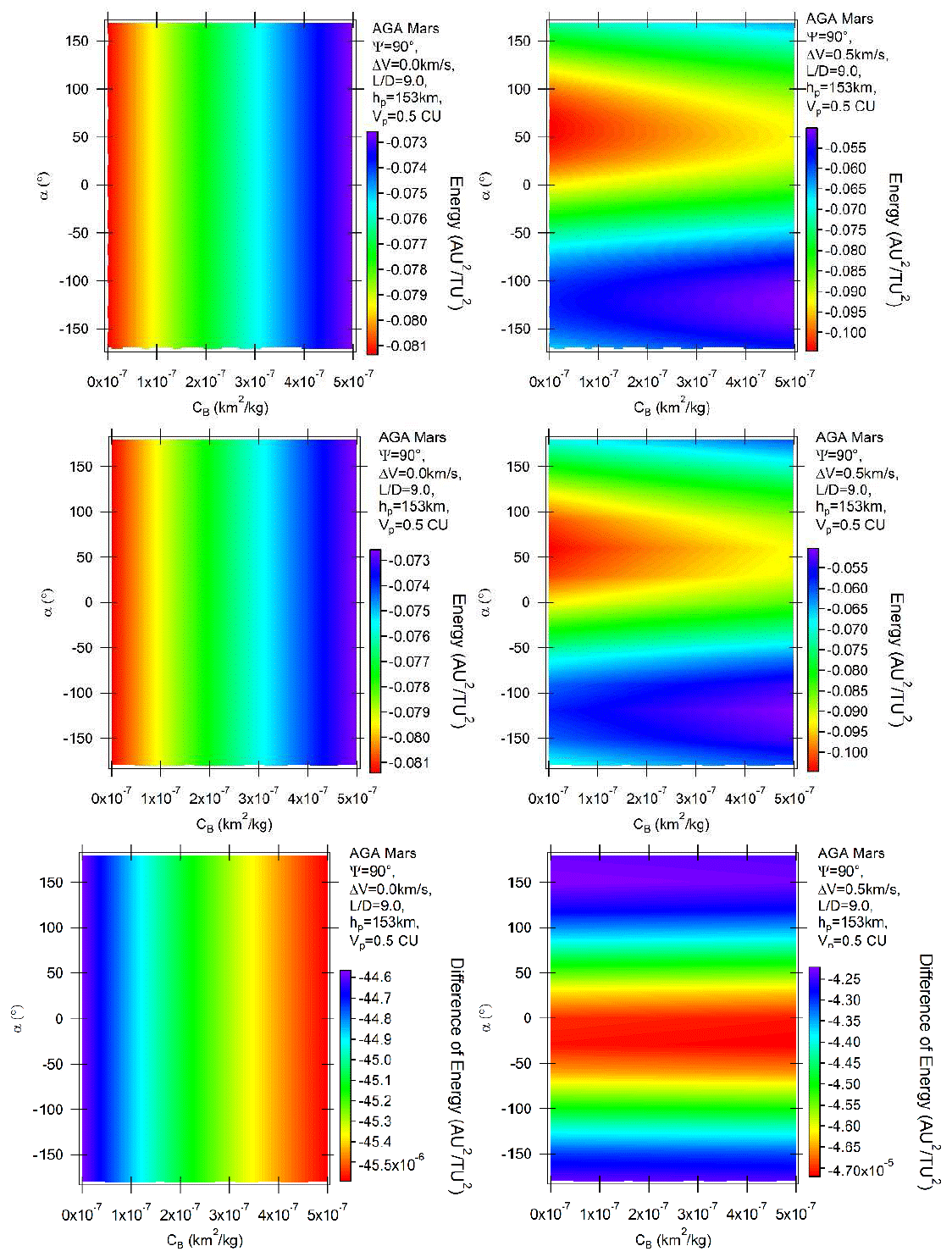
Fig. 3 Variation of energy per unit of mass as a function of the angle of attack for AGA with L/D = 9 and ψ = 90° for retrograde (above) and direct (middle) orbits. The difference between direct and retrograde orbits are shown in the bottom part of the figure. The color figure can be viewed online.
Next, Figure 4 shows the case of negative lift, which points in the direction of Mars. Maneuvers with negative lift increase the time the spacecraft stays in the atmosphere and reduce the periapsis altitude, therefore generating a higher influence of the drag force that reduces the energy. The values are L/D = −1 and ψ = 90° . Once again, the upper part of the figure represents retrograde orbits and the middle parts direct orbits. The unpowered retrograde orbits (upper left plot) have now an opposite behavior compared with the equivalent ones with positive lift. The energy losses now increase with the ballistic coefficient. The reason is the direction of the lift, which now points to Mars. In this way, both drag (directly) and lift (indirectly, by increasing the angle of curvature and so amplifying the effects of the gravity maneuver) act in the same direction, removing energy from the spacecraft.
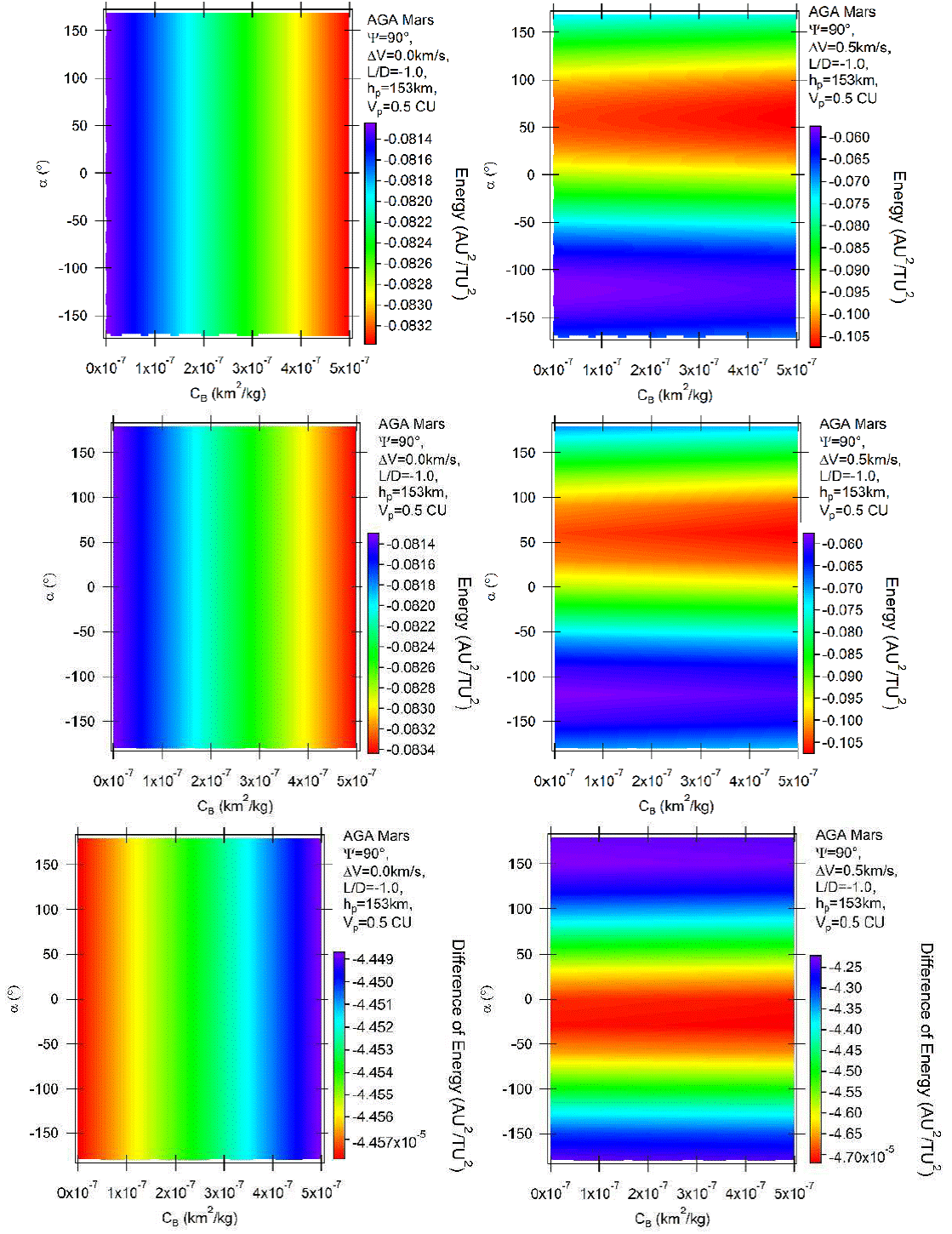
Fig. 4 Variation of energy per unit of mass as a function of the angle of attack for AGA with L/D = −1 and ψ = 90° for retrograde (above) and direct (middle) orbits. The differences between direct and retrograde orbits are shown in the bottom part of the figure. The color figure can be viewed online.
This inversion has been first observed in the present research. It is also valid for the Earth, but the situation of unpowered maneuvers with negative lift has not been considered in the literature for the Earth. The results for the direct orbits are similar to the previous cases, just with a difference of the order of 0.0001 canonical units. The bottom parts of the figure show the differences. Note that with negative lift the differences are slightly reduced with the increasing effects of the atmosphere. The powered maneuvers shown in the right side of Figure 4 also show interesting results. The locations of the maximum and minimum variations of energy are the same ones shown before, for the same reasons. There are more effects from the atmosphere, as already explained. This is shown by the inclinations of the border lines between two adjacent colors, in particular the yellow lines. They are no longer horizontal, as in the case of L/D = 1. For a fixed horizontal (α constant), it is clear (in the border lines between two colors), that the increase of the ballistic coefficient increases the losses of energy obtained from the maneuver. This is valid everywhere, although not as clear as in the borderlines. The reason is that now the negative lift increases the effect of the gravity part of the maneuver, which reduces energy, so adding to the drag, which also removes energy from the spacecraft. It means that the negative lift adds a dependency on the ballistic coefficient, due to the more active participation of the atmosphere in the total maneuver. The results for direct orbits confirm the existence of retrograde and direct orbits in Mars for this type of maneuver, with similar magnitudes. Piñeros & Prado (2017) did not simulate maneuvers with negative lift and impulses with magnitude of 0.5 km/s for the Earth, so a direct comparison is not possible. Once again, the bottom parts of the figure show the differences, giving details about the smaller variations observed.
Figure 5 shows the case of high negative lift, L/D = −9, combined with ψ = 90°. The unpowered maneuvers have exactly the same general behavior, with differences only in the magnitude of the maneuvers. L/D = −9 offers stronger effects and the interval of variations of energy is wider, from −0.098 to −0.082 canonical units, compared an interval from −0.0832 to −0.0814 canonical units for L/D = −1. This is of course caused by the larger effects obtained from the maneuver with higher lift. The powered maneuvers shown in the right side of Figure 5 confirm that the atmosphere has now a much larger participation in the maneuver. The lines are much more inclined compared to the case with L/D = −1. The appearance of the triangular shapes in the plots is caused by this stronger effect of the atmosphere. Note that now there are larger increases in the losses of energy with the ballistic coefficient. As occurred before, direct orbits also show very similar results.
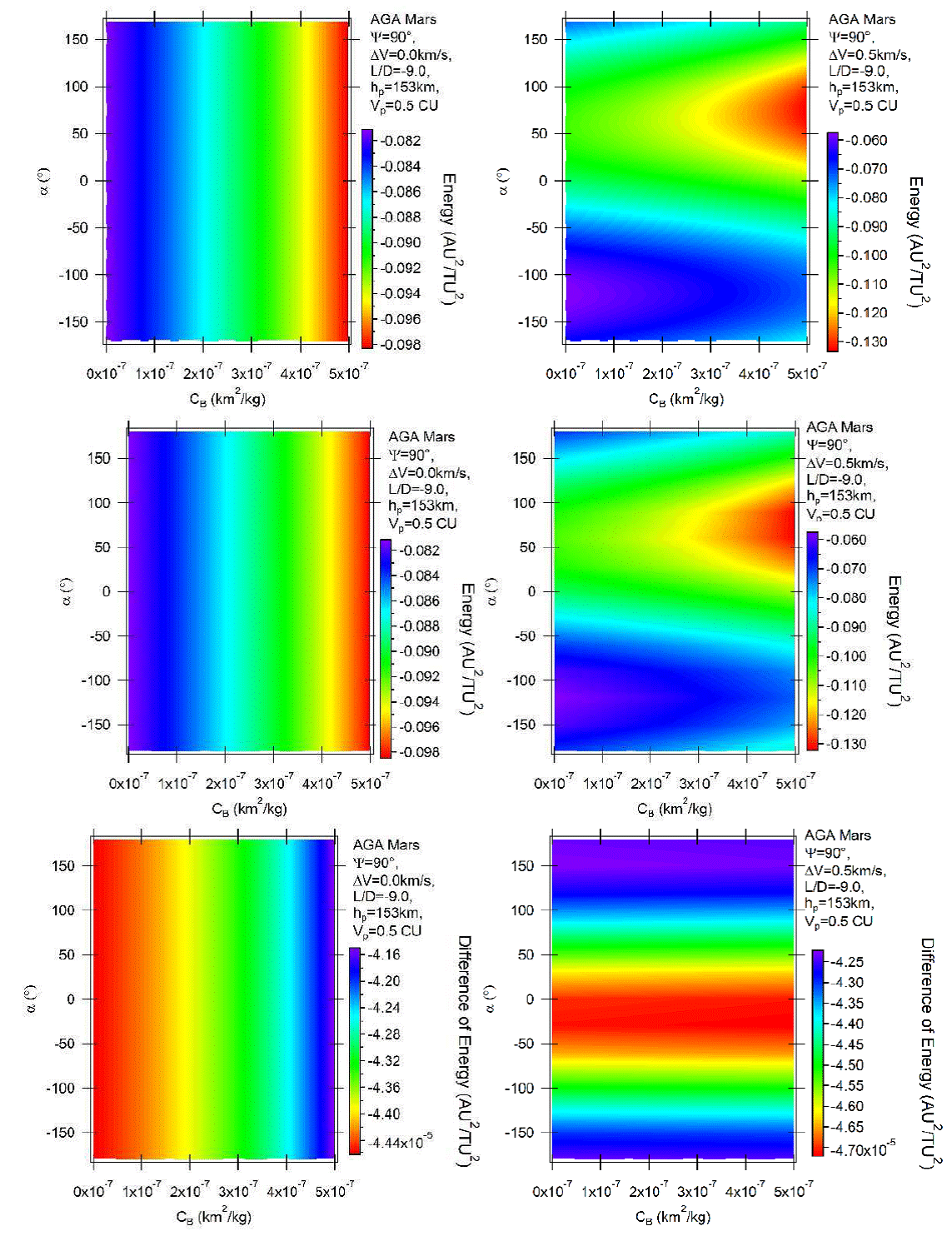
Fig. 5 Variation of energy per unit of mass as a function of the angle of attack for AGA with L/D = −9 and ψ = 90° for retrograde (above) and direct (middle) orbits. The differences between direct and retrograde orbits are shown in the bottom part of the figure. The color figure can be viewed online.
The next results show the situation where there are gains of energy, using ψ = 270◦ (Piñeros & Prado 2017). Figure 6 shows the results for L/D = −1. The unpowered maneuvers still generate plots with vertical lines, since there are no effects from the impulses. The gains of energy are larger for higher values of the ballistic coefficients. Note that the red color is on the left sides of the plots. The negative lift sends the spacecraft to Mars, increasing the gains of energy obtained from the pure gravity maneuver. Those gains are larger than the extra losses from the stronger drag, which remove more energy from the spacecraft. The magnitudes of those variations go from 0.0813 to 0.0821 canonical units, depending on the value of the ballistic coefficient. The powered maneuvers, shown at the right side of the plots, have little dependency on the ballistic coefficient. This is observed by looking at the almost horizontal borderlines between two adjacent colors. The impulses are dominating this situation. The maximum variations of energy are located near α = 120°. The reason is the same as already explained. The impulses have components in the direction of the motion of the spacecraft (adding energy directly to the spacecraft) and pointing to Mars (increasing the effects of the gravity part of the maneuver). The minimum variations of energy are located near α = −75°, where the impulses have components against the motion of the spacecraft and opposite to Mars. Retrograde and direct orbits show similar results, and exact comparisons with the Earth are not available in the literature for impulses of 0.5 km/s. Results for impulses with magnitude 0.3 km/s are shown in Piñeros & Prado (2017), and they have the same general behavior. The bottom parts of Figure 6 show that the gains of energy are slightly larger for the direct orbits.
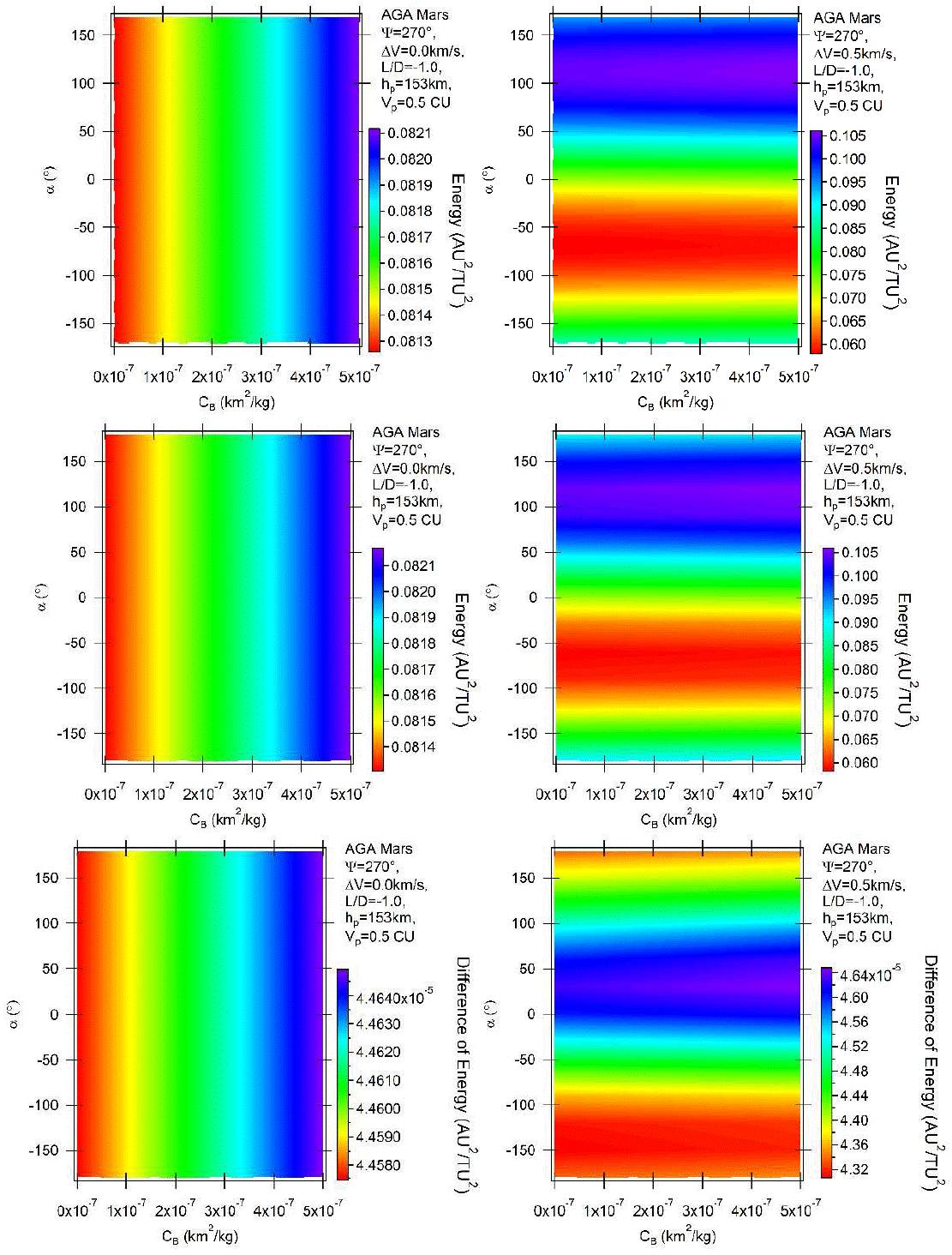
Fig. 6 Variation of energy per unit of mass as a function of the angle of attack for AGA with L/D = −1 and ψ = 270° for retrograde (above) and direct (middle) orbits. The differences between direct and retrograde orbits are shown in the bottom part of the figure. The color figure can be viewed online.
Next, Figure 7 shows the results for L/D = −9 and ψ = 270°. The same facts are confirmed. Differences show up in the magnitudes of the energy variations, which increase due to the higher value of the lift. Note that the variations of energy occur in the interval from 0.082 to 0.097 canonical units for the unpowered maneuver (it was from 0.0814 to 0.0822 canonical units when L/D = −1) and from 0.060 to 0.130 canonical units for the powered maneuver (it was from 0.060 to 0.105 canonical units whenL/D = −1). Note also the appearance of the triangular shapes in the powered maneuver indicating the stronger effects of the atmosphere. The energy gains increase with the ballistic coefficient, because the maneuver benefits from the atmosphere. As observed in the other cases, the results are similar for the direct and retrograde orbits.
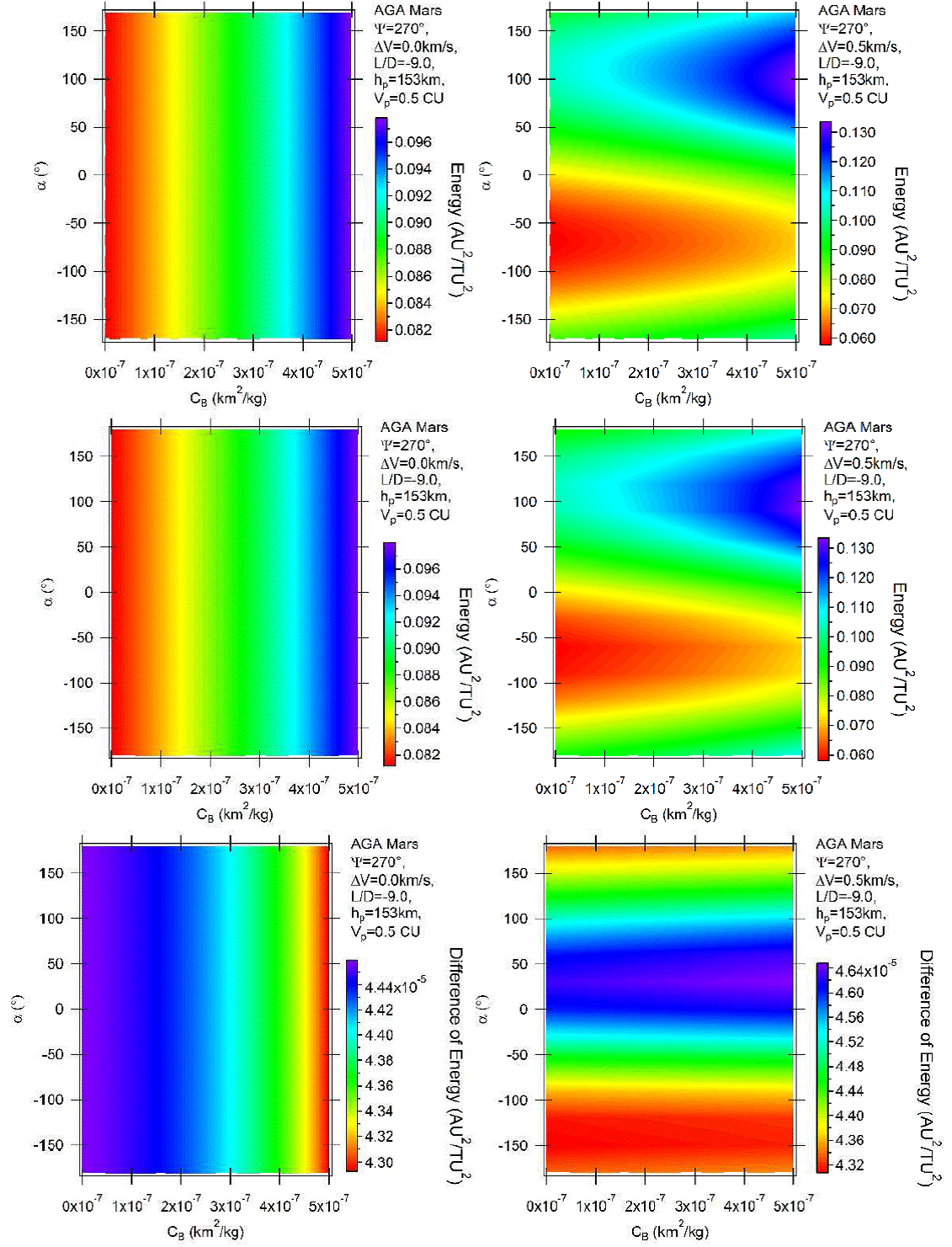
Fig. 7 Variation of energy per unit of mass as a function of the angle of attack for AGA with L/D = −9 and ψ = 270° for retrograde (above) and direct (middle) orbits. The differences between direct and retrograde orbits are shown in the bottom part of the figure. The color figure can be viewed online.
Considering now the results for the positive lift, Figures 8 and 9 show the situations where L/D = 1 and 9, respectively, with ψ = 270°. Direct and retrograde orbits show similar results, as indicated by the plots of the differences presented in the bottom parts of the figures. The gains of energy now decrease with the ballistic coefficient for the unpowered maneuvers, due to the combined actions of drag (removing energy directly due to friction with the atmosphere) and lift (sending the spacecraft away from Mars, so reducing the effects of the gravity part of the maneuver). For the powered maneuvers the pattern is repeated. There is little effect from the atmosphere for L/D = 1, which means that the border lines between two adjacent colors are horizontal, and larger effects for L/D = 9, where the same lines are inclined and the triangular shapes appear again.
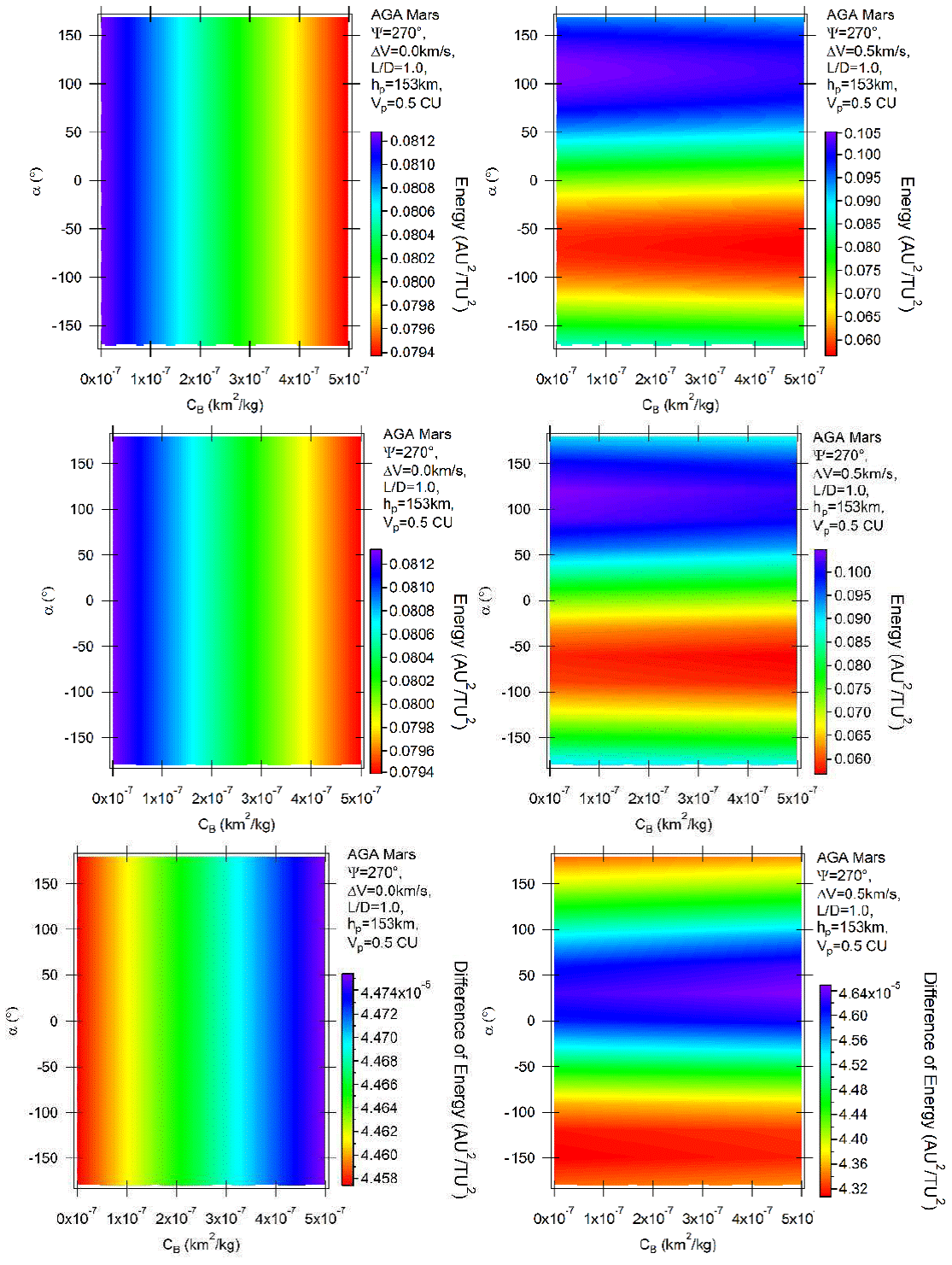
Fig. 8 Variation of energy per unit of mass as a function of the angle of attack for AGA with L/D = 1 and ψ = 270° for retrograde (above) and direct (middle) orbits. The differences between direct and retrograde orbits are shown in the bottom part of the figure. The color figure can be viewed online.
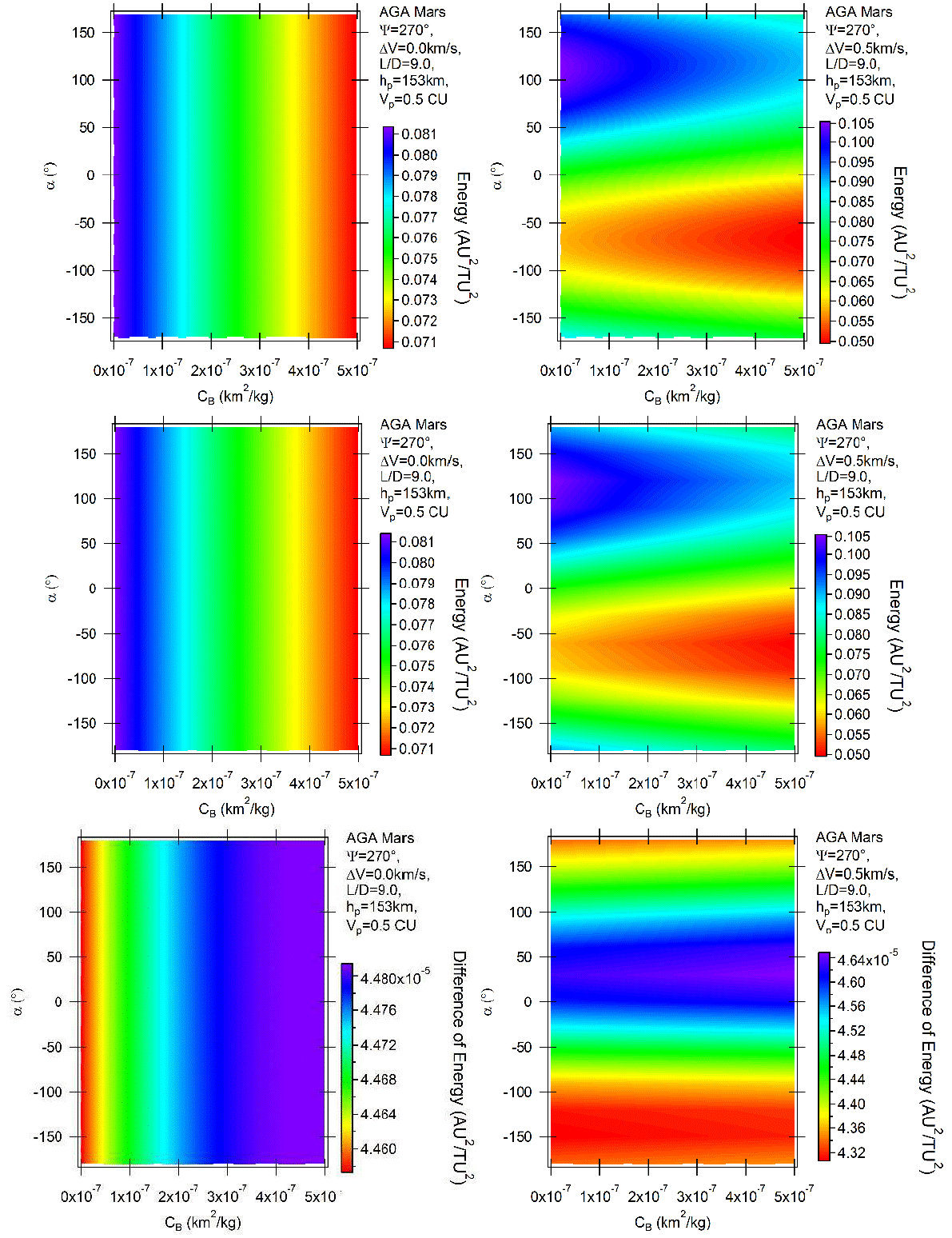
Fig. 9 Variation of energy per unit of mass as a function of the angle of attack for AGA with L/D = 9 and ψ = 270° for retrograde (above) and direct (middle) orbits. The differences between direct and retrograde orbits are shown in the bottom part of the figure. The color figure can be viewed online.
Another expected aspect that is verified and quantified in the present paper is the increase of the energy variations with the increase of the magnitude of the impulse. It is clearly visible when comparing similar plots constructed with different values of this magnitude. This is not much commented in the text, since it is easily expected, but the dynamics of this problem are complex and the quantification of these increases cannot be predicted without the numerical simulations made in the present paper.
Besides the effects in the variations of energy observed in the previous results, another important point to be considered is the effect of high and negative lift in the occurrence of collisions with Mars. It happens for L/D = −9, but for magnitudes of the impulses in the order of 1.0 and 1.5 km/s, with α in the region from 50° to 120° and a ballistic coefficient over 3 × 10−7 km2 /kg. The plots are not shown here because the main goal of the present paper is to study situations with smaller velocity increments, which have more practical applications, but it is an important fact to mention.
Figures 10 and 11 show some trajectories, with the goal of obtaining insight on their behavior. Figure 10 shows the initial direct trajectory (yellow, upper right) for an angle of approach of 90° and the retrograde initial trajectory (blue, lower left). When the two trajectories reach the pericenter the impulse is applied with variations in the angle that defines its direction. The trajectories are plotted to show these effects, because the direction of the impulse causes changes in the AGA trajectory. In the simulations shown in Figure 11, the results show trajectories with an angle of approach of 270°. The initial direct trajectory (yellow, lower left) and the retrograde initial trajectory (blue, upper right) are shown.
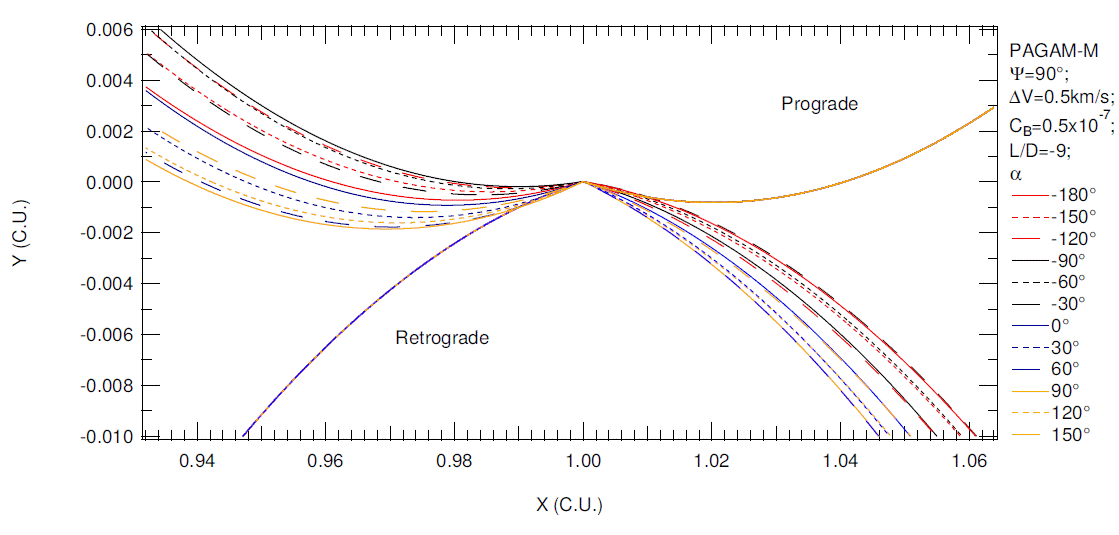
Fig. 10 Direct and retrograde trajectories for AGA with L/D = −9, CB = 0.5 × 10−7 and ψ = 90° for direct (above) and retrograde (below) orbits. The color figure can be viewed online.
4. Conclusions
The present paper studied the powered-aerogravity-assist maneuver around the planet Mars, which is a maneuver that combines lift and drag with an impulsive maneuver and the gravity of Mars. The main goal was to study the variations of energy as a function of the parameters involved, including the magnitude and direction of the impulse of the powered part of the maneuver; the periapsis distance; the angle and velocity of approach of the passage near Mars, and the ballistic coefficient that quantifies the effects of the atmosphere. Color maps showed the energy variations as a function of those parameters, in particular for geometries of maximum gains and losses of energy.
The distance and velocity at periapsis were fixed, because they are just scale factors, increasing or decreasing the effects of the atmosphere, so adding a multiplicative factor in the horizontal axis. Higher values for the L/D ratio were used, for both positive and negative values, of the order of 9, which are values obtained by waveriders.
The results showed very well the effects of the atmosphere, in particular the increased effect of the close approach by using negative lift (which points to the direction of Mars) and the decreased effect when using positive lift (which points opposite to Mars). Drag always removes energy directly from the spacecraft, but there are the indirect effects of modifying the geometry of the passage. They increase the angle of approach and decrease the periapsis distances, so they emphasize the effect of the close approach, which means that there are larger losses of energy for ψ = 90° and larger gains of energy for ψ = 270°. It was also shown that high negative values for the lift cause collisions of the spacecraft with Mars.
The complete maneuver generates lines that are not horizontal, showing the participation of both effects: impulsive maneuvers and atmosphere. For maneuvers with losses of energy, the maximum loss occurs when the impulse has a direction close to α = 60°, which gives a component opposite to the direction of motion of the spacecraft and another component pointing to Mars. Regarding maneuvers with gains of energy, the maximum variations were obtained for impulses applied close to the direction given by α = 120°. This means that the impulse has a component in the direction of the motion of the spacecraft and another component pointing to Mars.
High values for the lift, like L/D = 9, generate inclined lines of constant variation of energy, making “V” shapes in the plots, which measure the reductions of the effects in the maneuver. For negative lift (L/D = −9), the “V” shapes are inverted, showing the increased effect of the maneuver. For values of the magnitude of the impulse larger than 1.0 km/s, the impulse dominates the whole maneuver and the “V” shapes tend to disappear.
The increase of the energy variations as a function of the increase of the magnitude of the impulse for maneuvers around Mars was also noticed in the results shown here. This fact is expected, but its quantification is not trivial.
The results showed the existence of direct and retrograde orbits around Mars; they are similar in terms of variations of energy, for the unpowered and powered maneuvers with impulses of magnitude of up to 0.5 km/s. The differences in terms of the energy variations are of the order of 0.0001 AU2/TU2. Magnitudes above this value generate a large number of collisions with Mars. Compared to the Earth, Mars gives larger variations of energy for similar conditions.
The results also showed that Mars causes about twice the effects observed for the Earth, which means that Mars is a better source of energy for the powered-aero-gravity-assist maneuver. It was also observed that unpowered retrograde orbits with positive lift for ψ = 90◦ have opposite behaviors, compared to the equivalent ones with positive lift. The energy losses increase with the ballistic coefficient. The reason is that negative lift points to Mars, so drag and lift act in the same direction of removing more energy from the spacecraft.











 nueva página del texto (beta)
nueva página del texto (beta)