Introducción
Recientemente la aplicabilidad de marcos de concreto reforzado con contraventeo metálico se ha estudiado no únicamente desde un enfoque de reparación, sino desde el punto de vista de diseño de edificaciones nuevas. Algunos investigadores se han enfocado en el estudio del comportamiento sísmico y el desarrollo de parámetros de diseño para diferentes configuraciones de contraventeo (Maheri y Akbari 2003, Maheri y Hadjipour 2003, Youssef et al. 2007, Maheri y Ghaffarzadeh 2008, Godínez-Domínguez y Tena-Colunga 2010, Godínez 2010, Godínez-Domínguez y Tena-Colunga 2012) demostrando que existe influencia de diversos factores en el comportamiento de dichos sistemas estructurales. Uno de los factores que influyen en el comportamiento sísmico de los marcos contraventeados radica en el esquema de contraventeo empleado (Figura 1), presentándose diferencias tanto a nivel local como global (Maheri y Akbari 2003). En un estudio previo (Godínez 2010, Godínez y Tena 2010) se estudiaron con detalle marcos de concreto reforzado con contravientos chevrón (tipo V invertida) exclusivamente. Sin embargo, los contravientos concéntricos en X han sido ampliamente utilizados en México (Del Valle et al. 1988, Foutch et al. 1989, etc.) y siguen empleándose a nivel nacional. Por lo tanto, el estudio de sistemas estructurales con un esquema de contraventeo en X permite complementar el panorama del arreglo de contravientos más comúnmente utilizados en México para estructuras con elevaciones típicas en las zonas de interés.
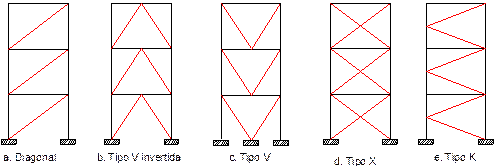
Figura 1 Principales configuraciones de marcos con contraventeo concéntrico (adaptada de Bruneau et al. 1998)
El objetivo principal de este estudio radica en la determinación de la influencia del esquema de contraventeo en parámetros de diseño tales como: factores de reducción por sobrerresistencia, distorsiones asociadas al estado límite de servicio y de colapso, capacidades de deformación globales y de entrepiso y, aporte mínimo de columnas al cortante resistente de entrepiso para fomentar mecanismos de colapso congruentes con el esperado de columna fuerte-viga débil-contraviento más débil. Para lograr dicho objetivo, se requiere contar con información relativa al diseño y comportamiento de marcos con contraventeo en cruz (considerando los mismos casos de estudio que para marcos con contraventeo tipo chevrón), para su posterior comparativa. Por lo anterior, en la primera parte de este artículo se reportan aspectos relacionados con el diseño y evaluación del comportamiento de marcos dúctiles de concreto reforzado con contraventeo concéntrico en cruz, en que se emplea la metodología de diseño por capacidad propuesta para marcos con contravientos chevrón realizada por Godínez (2010) y adaptada a los lineamientos de las Normas Técnicas Complementarias para Diseño y Construcción de Estructuras de Concreto (NTCC-04), así como a las Normas Técnicas Complementarias para Diseño por Sismo (NTCS-04) del Reglamento de Construcciones para el Distrito Federal vigente (RCDF-04).
Requisitos reglamentarios
De acuerdo con las Normas Técnicas Complementarias para Diseño por Sismo (NTCS-04), las estructuras con base en marcos contraventeados deben analizarse considerando la contribución de la resistencia a fuerza cortante tanto del marco como del sistema de contraventeo (Figura 2). En el caso de estructuras con comportamiento dúctil, en cada entrepiso los marcos deben ser capaces de resistir, sin contar con contravientos, cuando menos el 50 por ciento de la fuerza sísmica actuante.
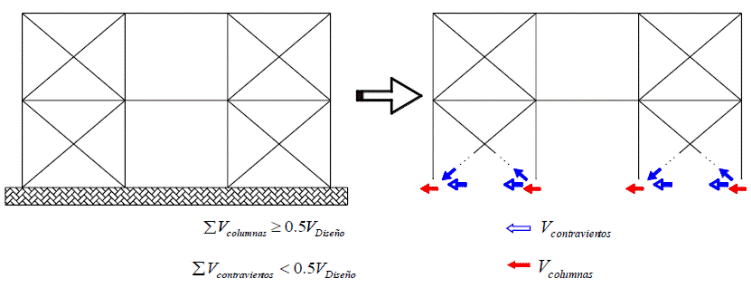
Figura 2 Mecanismo resistente a fuerza cortante en marcos con contraventeo de acuerdo con las NTCS-04
Para valorar la pertinencia de este límite, al igual que lo realizado para el caso de marcos con contraventeo metálico en configuración chevrón (Godínez 2010, Godínez y Tena 2010), se diseñaron marcos con contraventeo metálico en cruz que, además de cumplir con este balance, satisficieran dos balances más, aspecto que se comenta en la sección siguiente.
Estudio de marcos planos con contraventeo metálico en cruz
Modelos de análisis
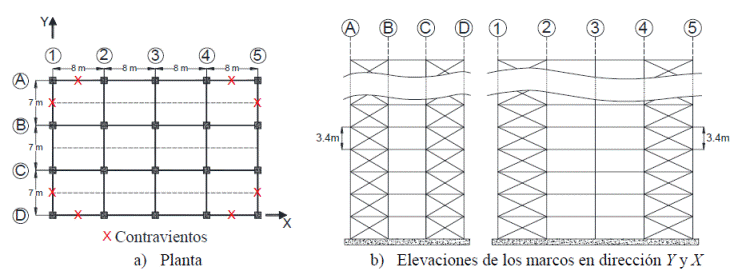
Congruente con el estudio de referencia (Godínez 2010), los marcos analizados corresponden a una estructura regular tridimensional con uso supuesto para albergar oficinas. El edificio cuenta con una planta rectangular de 21 m de ancho (dirección Y) y 32 m de largo (dirección X) en la que los marcos periféricos se encuentran contraventeados en sus crujías exteriores. El edificio cuenta con cuatro crujías en la dirección X y tres en la dirección Y con claros de 8 m y 7 m respectivamente (Figura 3). En la dirección X existen vigas secundarias. La altura típica de entrepiso es de 3.40 m. Por lo tanto, las alturas totales de los modelos de 4, 8, 12, 16 y 20 niveles son 13.6, 27.2, 40.8, 54.4 y 68.0 m respectivamente.
La gama de alturas estudiada permite obtener resultados representativos para un intervalo de periodos amplio, lo cual es deseable para un mejor entendimiento del comportamiento estructural conforme se incrementa la altura (H) de los marcos y valorar cómo impacta la esbeltez (H/L, L representa la longitud del marco en la dirección de análisis) en el comportamiento sísmico de estructuras que cumplen con el resto de las condiciones de regularidad; así como valorar su efecto en algunos parámetros de diseño, como son los factores de reducción por sobrerresistencia o las distorsiones de entrepiso asociadas a los estados límite de servicio y colapso.
Casos de estudio
Para contar con un marco de comparación, se analizaron marcos planos con contraventeo en cruz considerando distintas variantes, basadas en el aporte que a la resistencia ante carga lateral brindan las columnas con respecto a los contravientos. Como se comentó, lo anterior se hizo en atención a lo estipulado en las NTCS-04, donde se establece que para el empleo de un factor de comportamiento sísmico Q=4 (adoptado en el diseño de todos los modelos) en estructuras cuya resistencia en todos los entrepisos es suministrada por marcos contraventeados, en cada entrepiso los marcos deben ser capaces de resistir, sin contar con contravientos, cuando menos el 50 por ciento de la fuerza sísmica actuante (Figura 2).
Con la finalidad de estudiar si el balance de resistencia estipulado en las NTCS-04 es razonable o no para obtener un comportamiento dúctil en marcos con contraventeo metálico en cruz, y valorar cómo dicho balance y el esquema de contraventeo pueden afectar el comportamiento estructural del sistema, tanto a nivel global como a nivel local, se consideraron los tres siguientes casos:
Caso I. Cuando las columnas de los marcos resisten un porcentaje menor al 50% de la carga sísmica actuante (aproximadamente 25%), lo cual no está permitido en las NTCS-04 para comportamiento dúctil.
Caso II. Cuando la condición estipulada en las NTCS-04 para comportamiento dúctil se cumple al límite, es decir, el 50% de la carga actuante es resistida por las columnas de los marcos y el 50% por los contravientos.
Caso III. Cuando un porcentaje mayor de carga lateral es resistida por las columnas de los marcos (aproximadamente 75%)
Metodología de diseño y consideraciones de análisis
Los modelos para el análisis estructural se realizaron con el programa de análisis SAP2000 en su versión 14.0 (SAP2000 2009). Para el cálculo de las fuerzas laterales para el diseño de los marcos se llevó a cabo un análisis modal espectral, incluyendo los efectos P-Δ.
Para el diseño de los elementos sismorresistentes se empleó una metodología basada en conceptos por capacidad, donde los elementos estructurales se diseñan por resistencia del más débil al más fuerte, por lo que para obtener un mecanismo de colapso columna fuerte - viga débil - contraviento más débil, la secuencia de diseño recomendable es: 1) contravientos, 2) vigas, 3) columnas y, 4) conexiones. La metodología de diseño empleada se deriva de una serie de análisis estáticos no lineales ante carga monótona creciente de marcos planos con contraventeo chevrón de entre cuatro y 24 niveles, las cual se describe con detalle en Godínez y Tena (2009 y 2011), Godínez-Domínguez y Tena-Colunga (2008 y 2010) y Godínez (2010). Para el caso de los marcos con contraventeo en cruz, se realizaron las adaptaciones pertinentes (Godínez 2012), pues el hecho de contar con este esquema de contraventeo modifica la forma en que se transmiten las cargas a vigas, columnas y conexiones respecto al caso de marcos con contraventeo chevrón.
Congruente con el estudio de referencia, para la elaboración de los modelos de análisis estructural se consideró el aporte de la losa en rigidez y resistencia, es decir, al modelar las vigas, éstas se hicieron como vigas L. Las losas fueron previamente diseñadas, como es costumbre, para tomar cargas verticales y satisfacer estados límites de deformación y de servicio. Además, de acuerdo con lo recomendado en la literatura (por ejemplo, Horvilleur y Cheema 1994, Tena 2007), en los análisis se consideró que la rigidez en los nudos es 50% de la que tendrían si fueran infinitamente rígidos a flexión.
Zona de estudio
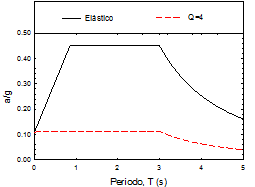
Las estructuras en estudio se ubicaron para su diseño en la zona III-b. En la Figura 4 se muestra el espectro elástico de diseño sísmico del cuerpo principal, así como el reducido por concepto de ductilidad para Q=4 (factor de comportamiento sísmico empleado en los diseños).
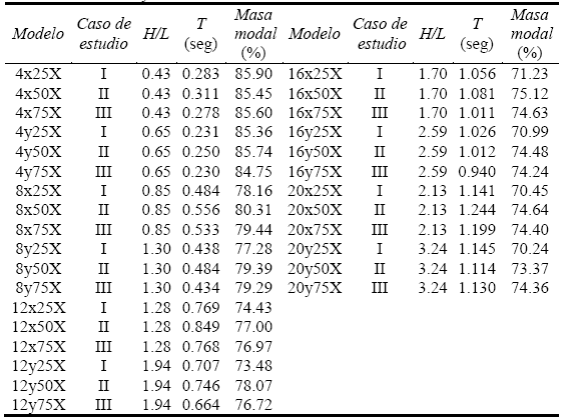
Como es normal, las demandas de aceleración a las que está sujeto cada modelo dependen de sus características dinámicas (periodo). La mayoría de los modelos de mayor altura (12 a 20 niveles), se encuentran ubicados en la meseta del espectro Tablas 1 y 2 , lo cual indica que están sujetos a las máximas demandas.
Tabla 2 Casos de estudio y características dinámicas de los modelos con contraventeo chevrón (Godínez 2010)
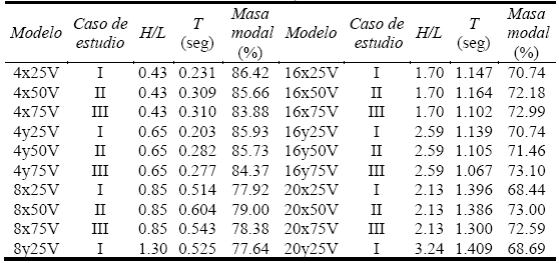
Aspectos generales de los diseños
La sección de columnas se varió de acuerdo al número de niveles del marco estudiado. En los marcos de cuatro niveles, la sección de columnas permaneció constante en altura, al igual que las vigas y contravientos. Para los marcos de 8 a 16 niveles, la variación de secciones de columnas y vigas se realizó cada cuatro niveles, alternando la variación de las secciones en el caso de los contravientos, los cuales variaron de espesor cada tres niveles, manteniendo su sección transversal. En los modelos de 20 niveles la variación de secciones de columnas y vigas se realizó cada cinco niveles, y la variación del espesor de la sección de los contravientos quedó determinada de tal manera que las secciones propuestas estuviesen diseñadas lo más justas posibles.
Lo anterior obedece a tratar de evitar el crear planos de debilidad en algún entrepiso, pues de los análisis estáticos no lineales realizados en marcos con contraventeo chevrón se observó, que la práctica de variar en el mismo entrepiso las secciones de vigas, columnas y contravientos conducía a la posible generación de pisos débiles, ocasionando fallas no deseadas y reduciendo significativamente la ductilidad del sistema (Godínez 2010).
El dimensionamiento de las columnas se realizó siempre con base en el balance de resistencia/rigidez seleccionado. Para el cálculo del refuerzo transversal, prácticamente en todos los casos rigió el criterio de resistencia por fuerza cortante y no el de confinamiento. En la mayoría de los armados por flexión de columnas se requirieron cuantías mínimas, esto debido a que se tienen secciones más robustas de lo requerido por resistencia. En la determinación de los armados por flexión y cortante en vigas, en general, rigió el criterio de resistencia.
En todos los casos los contravientos son secciones cajón de acero A-36, como es práctica común tanto en el caso de proyectos de refuerzo estructural (concreto o acero), como para el caso de diseños nuevos de estructuras metálicas.
Para identificar los distintos diseños y facilitar su posterior comparación, se utilizó la siguiente nomenclatura general para los modelos: NdppT, donde la N indica el número de niveles del marco, d indica la dirección de análisis (x o y) conforme a la planta de los modelos (Figura 3a), los dos caracteres (pp) indican el porcentaje de fuerza cortante que aportan las columnas del marco, y finalmente T indica el tipo de contraventeo considerado (V para contraventeo chevrón y X para contraventeo en cruz). Por ejemplo, el modelo 12y75X, identifica el diseño de un marco de doce niveles en la dirección Y de la planta de la Figura 3a, donde las columnas aportan aproximadamente el 75% de la resistencia a fuerza cortante en el entrepiso y cuenta con contravientos metálicos dispuestos en cruz. Así, se diseñaron los siguientes marcos con contraventeo en cruz: 4y25X, 4y50X, 4y75X, 4x25X, 4x50X, 4x75X, 8y25X, 8y50X, 8y75X, 8x25X, 8x50X, 8x75X, 12y25X, 12y50X, 12y75X, 12x25X, 12x50X, 12x75X, 16y25X, 16y50X, 16y75X, 16x25X, 16x50X, 16x75X, 20y25X, 20y50X, 20y75X, 20x25X, 20x50X, 20x75X (Tabla 1).
En las Tablas 1 y 2 se resumen respectivamente para cada modelo con contraventeo en cruz y chevrón, el caso de estudio, las propiedades dinámicas y la masa asociada al primer modo de vibrar. Es importante mencionar que todos los resultados de los modelos con contraventeo metálico tipo chevrón (para los mismos balances de resistencia y número de niveles indicado) provienen del estudio de referencia desarrollado por Godínez (2010).
Consideraciones realizadas en los análisis estáticos no lineales
Se realizaron análisis estáticos no lineales ante cargas monótonas crecientes ("pushover"), para los cuales se empleó el programa DRAIN-2DX (Prakash et al. 1992). Por simplicidad y congruencia con lo realizado en el estudio de referencia, en todos los análisis se empleó el vector de cargas correspondiente al primer modo de vibración. Lo anterior se realizó tomando en cuenta que: (a) los modelos en estudio están en el intervalo de los cuatro a los 20 niveles, (b) la masa modal asociada al modo fundamental de vibración es, en general, superior al 70% en el caso de los modelos con comportamiento dúctil (Tablas 1 y 2 ) y, (c) los sistemas estudiados tienen una rigidez lateral importante, por lo que el efecto de los modos superiores no tiene impacto significativo en la respuesta estructural, tal y como se comenta con detalle en Godínez (2010) y Godínez y Tena (2011).
Se incluyen en todos los casos los efectos P-∆ en columnas y diagonales y se ignora la interacción suelo estructura. El efecto de la interacción suelo estructura no se considera en este estudio para evitar introducir mayor cantidad de variables que compliquen la interpretación de los resultados.
En las secciones posteriores, se presentan exclusivamente los resultados asociados a aquéllos modelos en que se consideran fuentes adicionales de resistencia. Los criterios para la determinación de dichas resistencias se describen con detalle en Godínez y Tena (2007) y Godínez (2010 y 2012).
Resultados de los análisis estáticos no lineales
De los análisis estáticos no lineales se obtuvieron las curvas normalizadas cortante-distorsión globales (cortante basal vs distorsión de azotea) y de entrepisos (V/WT vs Δ), así como los mapeos de rotaciones plásticas acumuladas asociadas al colapso teórico de cada modelo. Durante el post-proceso, la distorsión última se limitó en función de la rotación máxima que los elementos estructurales son capaces de desarrollar, así como de las longitudes de pandeo calculadas para los contravientos.
Las capacidades de rotación teóricas de los elementos (vigas y columnas) se determinaron mediante el cálculo de las curvas momento-curvatura empleando el programa Biax (Wallace y Moehle 1989). La determinación de la magnitud del acortamiento que pueden sufrir las diagonales de contraventeo al momento del pandeo se hizo con base en la propuesta de Kemp (1996), la cual se apoya en pruebas experimentales realizadas por varios investigadores a nivel mundial.
Para la determinación de los factores de reducción por sobrerresistencia (R), las capacidades de deformación inelástica globales y de entrepiso (μ), las distorsiones de fluencia de entrepiso equivalentes (Δy ), y distorsiones máximas (Δmax ), se obtuvieron curvas bilineales idealizadas de las curvas cortante-distorsión reales (Figura 5), conforme a lo especificado en la literatura (Newmark y Hall 1982, FEMA-273 1997).
Envolventes de distorsión de entrepiso máximas
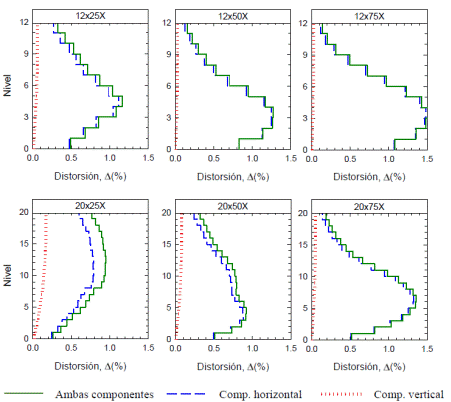
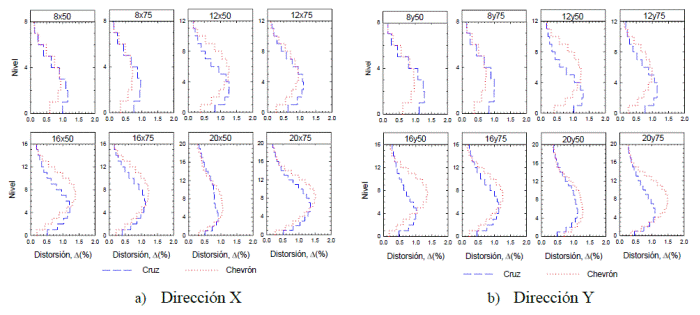
Como se comenta en Godínez y Tena (2011), la distorsión de entrepiso de cualquier edificio con base en marcos que ha sido diseñado de manera rigurosa, tomando en cuenta los grados de libertad de traslación, de rotación y de deformación axial, y que además incluye los efectos de segundo orden o P-Δ, se debe calcular también rigurosamente tomando en cuenta: (1) la distorsión angular debida a la diferencia de los desplazamientos laterales de niveles contiguos divididos por la altura, también conocida como la distorsión por cortante o "componente horizontal" de la distorsión y, (2) la distorsión debida a la flexión general del marco en la dirección de análisis, calculada como el ángulo debido a la diferencia entre la extensión y el acortamiento de las columnas extremas del marco dividida entre la distancia existente entre ambas columnas. A esta distorsión también se le conoce como "componente vertical" de la distorsión. Por ello, en este trabajo las distorsiones de entrepiso reportadas de la Figura 6 en adelante toman en cuenta esta distorsión total: la suma de la distorsión por cortante más la debida a la flexión general de los marcos.
Con la finalidad de discernir qué tanto se pierde o no al despreciar o incluir la distorsión por flexión general ("componente vertical"), se evaluó para cada marco con contraventeo en cruz su impacto relativo. Con fines ilustrativos, en la Figura 6 se presentan las envolventes de distorsiones de entrepiso máximas de los modelos de 12 y 20 niveles en la dirección X de análisis y: (a) sólo se considera la distorsión por cortante ("componente horizontal", línea discontinua), (b) sólo se considera la distorsión por flexión general ("componente vertical", línea punteada) y, (c) se considera la distorsión total: por cortante más flexión general ("ambas componentes", línea continua). De las gráficas de la Figura 6 se confirma que, como es bien sabido, la importancia de la distorsión por flexión (componente vertical) se incrementa con la altura y no menos importante, su impacto crece a medida que los contravientos tienen un mayor aporte a la rigidez y resistencia (modelos 12x25X y 20x25X) y disminuye a medida que los marcos tienen un mayor aporte en rigidez y resistencia (modelos 12x75X y 20x75X). Lo anterior es congruente con lo observado para marcos con contraventeo chevrón (Godínez y Tena 2011).
Curvas cortante-distorsión
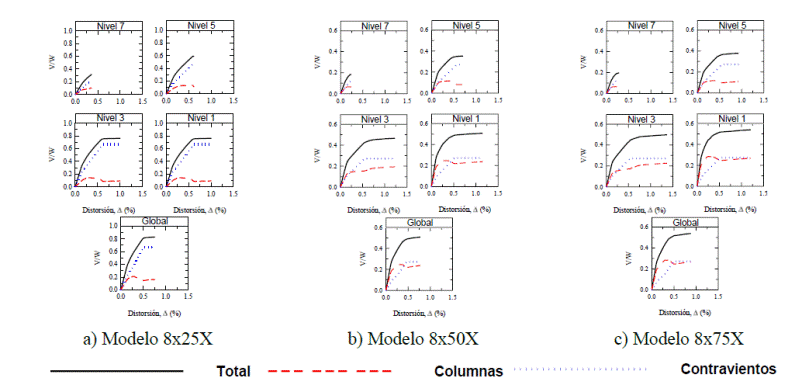
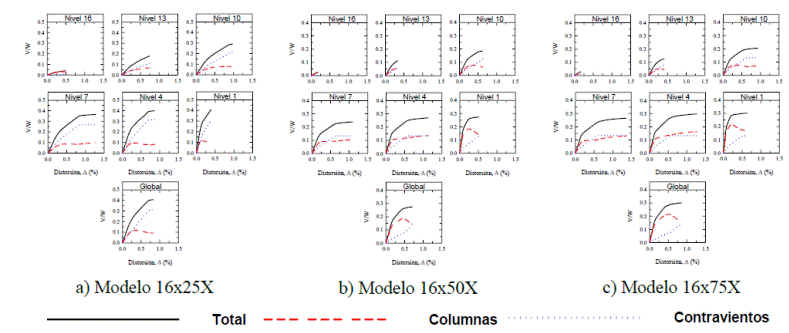
En las Figuras 7 y 8 se presentan de manera ilustrativa las curvas cortante-distorsión para algunos de los modelos con contraventeo en cruz de 8 y 16 niveles, las cuales son representativas del conjunto de modelos estudiados. Las curvas cortante-distorsión de cada modelo con contraventeo chevrón y en cruz estudiado se reportan con detalle en Godínez (2010 y 2012), respectivamente.
En las curvas cortante-distorsión se muestran por separado la contribución de cada componente (columnas y contravientos) al cortante resistente en cada entrepiso y a nivel global. También, se muestra la suma de los dos componentes, la cual representa la resistencia lateral total del marco contraventeado. Conforme a lo reportado por Maheri y Akbari (2003) y por Ghaffarzadeh y Maheri (2006), este procedimiento es adecuado para el cálculo de la resistencia lateral total del sistema dual.
De las curvas cortante-distorsión se observa que la respuesta global del sistema, representada por la curva cortante basal vs distorsión promedio (calculada con base en el desplazamiento de azotea), no es siempre representativa del comportamiento de cada entrepiso, pues por ejemplo, para algunos casos (modelos 8x25X, Fig. 7a y 16x75X, Fig. 8c) en los niveles superiores el comportamiento es prácticamente elástico hasta el último paso, en tanto que los pisos inferiores son capaces de desarrollar mayores distorsiones y niveles de cortante al ingresar a su intervalo de comportamiento plástico (mismo efecto observado en los marcos con contraventeo chevrón).
Se observa que, en general, las mayores distorsiones se desarrollan en los niveles intermedios (modelos de ocho a 16 niveles) y en el primer tercio de la altura para los modelos de 20 niveles (no mostrado). Como se observará en secciones posteriores, es en dichos niveles donde los elementos estructurales experimentan las mayores rotaciones plásticas.
De las curvas cortante distorsión se aprecia que, para los casos en que el balance de resistencia considerado demanda una mayor contribución del sistema de contraventeo al cortante resistente (por ejemplo, modelo 16x25X, Fig. 8a), existe una menor capacidad de deformación inelástica en los entrepisos superiores respecto al caso en que el balance considerado demanda un mayor aporte de las columnas (por ejemplo, 16x75X, Fig. 8c), en el que se observa una mejor distribución del comportamiento inelástico en la altura del marco. Lo anterior es deseable para una mayor disipación de energía. Este efecto se observa también en los modelos de menor altura (Godínez 2012). Lo anterior, es también congruente con lo previamente reportado para marcos con contraventeo chevrón (Godínez 2010, Godínez y Tena 2010 y 2011).
De las curvas que definen la respuesta global de algunos modelos (Figuras 7 y 8 ), se observa que el comportamiento que presentan las columnas y contravientos difiere entre sí conforme la estructura ingresa en mayor medida a su intervalo de comportamiento plástico. Para la mayoría de los modelos, posterior a la primera fluencia, el porcentaje de fuerza cortante que resisten los contravientos crece (pendiente positiva), en tanto que el de las columnas disminuye (pendiente negativa). Este efecto se observó también en los modelos con contraventeo chevrón pero de forma más pronunciada, y se discute con detalle en Godínez-Domínguez y Tena-Colunga (2011).
Fluencias y rotaciones plásticas en elementos estructurales
En esta sección se presentan figuras que ilustran la ubicación y magnitud de las rotaciones plásticas acumuladas de los modelos estudiados con base en los resultados de los análisis estáticos no lineales. La magnitud de las rotaciones inelásticas en vigas y columnas se muestra mediante una escala de colores usando una marca circular; asimismo, las extensiones y acortamientos en diagonales se muestran mediante una segunda escala de colores empleando un marca en forma de ovalo.
De esta sección en adelante, para facilitar la comparación cruzada de resultados y valorar el efecto del esquema de contraventeo en la respuesta estructural, se presentan algunos de los resultados previamente obtenidos para marcos con contraventeo chevrón, los cuales se reportan y discuten con detalle en Godínez-Domínguez y Tena-Colunga (2010), Godínez (2010) y, Godínez y Tena (2011).
En la Figura 9 se muestra, para ambas configuraciones de contraventeo, el mapeo de rotaciones plásticas acumuladas correspondiente al colapso teórico de los modelos de cuatro a 20 niveles en dirección X, cuando las columnas aportan aproximadamente el 25% de la fuerza cortante total; además, en las Figuras 10 y 11 se muestra lo correspondiente a los casos en que las columnas aportan aproximadamente el 50% y 75% de la fuerza cortante total. Los mapeos de rotaciones plásticas de todos los modelos con contraventeo en cruz se reportan en Godínez (2012).
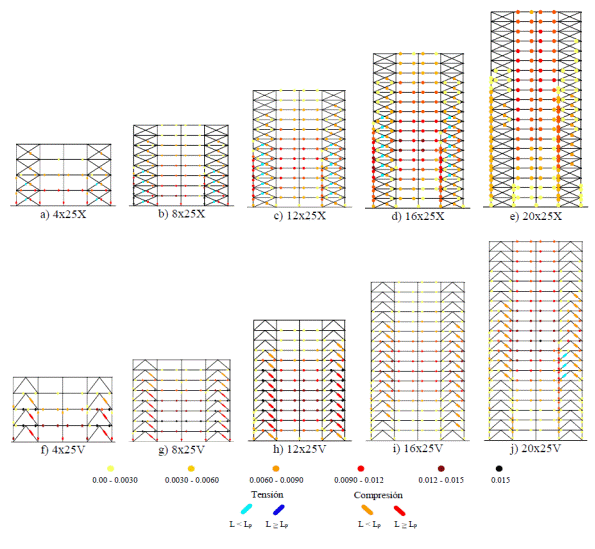
Figura 9 Rotaciones plásticas acumuladas de los modelos en que las columnas aportan aproximadamente 25% de la resistencia a cortante
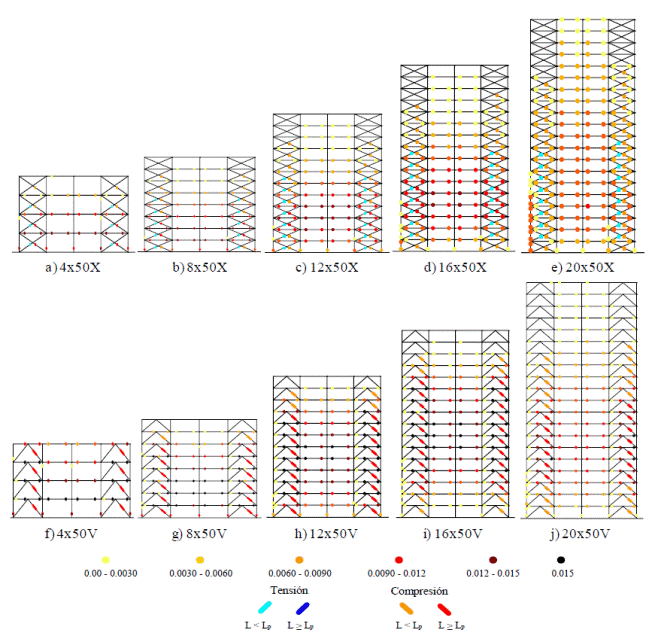
Figura 10 Rotaciones plásticas acumuladas de los modelos en que las columnas aportan aproximadamente 50% de la resistencia a cortante

Figura 11 Rotaciones plásticas acumuladas de los modelos en que las columnas aportan aproximadamente 75% de la resistencia a cortante
De los mapeos de fluencias se observa que existe una variación en la ubicación de las mayores deformaciones inelásticas con base en la altura de los modelos; por ejemplo, para los marcos con contraventeo en cruz, en los modelos de cuatro niveles, entrepisos uno a tres (niveles dos a tres para marcos con contraventeo chevrón); en el caso de los modelos de ocho niveles, entrepisos uno a cinco (uno a seis para marcos chevrón); para el caso de los modelos de 12 niveles, entrepisos dos al siete (mismos entrepisos para marcos chevrón), y para los modelos de 16 niveles, entrepisos dos al diez (mismos entrepisos para marcos chevrón). En los modelos de 20 niveles, para ambas configuraciones de contraventeo, el mayor trabajo inelástico se concentra en la primera mitad de la altura.
Para cumplir con el balance en que las columnas aportan únicamente el 25% de la fuerza cortante resistente total (Fig. 9), las secciones de los contravientos deben ser muy robustas (con sobrerresistencias locales elevadas), reduciendo la ductilidad global del sistema, lo cual es más evidente conforme se incrementa la altura de los modelos (Figs. 7a y 8a ). Para ambas configuraciones de contraventeo, se observa que el mecanismo de falla columna fuerte-viga débil-contraviento más débil no se garantiza (Fig. 9). Para este caso de estudio, a diferencia de los modelos con contraventeo chevrón, en los que la primera articulación plástica ocurre usualmente en una columna, en los marcos con contraventeo en cruz generalmente ocurre en una viga (pero en ningún caso en los contravientos). En estos modelos, existen rotaciones en algunas columnas, cuya distribución y magnitud es superior a la observada para los otros dos balances de resistencia (Figs. 9a 11 ). En ocasiones existen articulaciones en ambos extremos de una misma columna, situación poco deseable. Lo anterior, se debe a que para estos modelos, en que se considera que el sistema de contraventeo representa la línea de defensa principal del sistema dual, una vez que se presenta el pandeo de las diagonales, los elementos del marco de concreto reforzado no son capaces de resistir adecuadamente las cargas producidas por efecto de la redistribución de fuerzas, pudiendo presentarse modos de falla indeseables, como los asociados a pisos débiles.
Para los modelos en que las columnas aportan aproximadamente el 50% de la fuerza cortante total (resistencia mínima estipulada en las NTCS-04 para comportamiento dúctil) y aquéllos en que aportan aproximadamente 75% de la fuerza cortante total (Figuras 10 y 11 ), para ambos esquemas de contraventeo, la distribución y magnitud de las rotaciones plásticas es similar; sin embargo, la magnitud y distribución de las rotaciones plásticas en columnas decrece conforme se incrementa el aporte de las columnas al cortante resistente. A diferencia de lo observado en marcos con contraventeo chevrón, en donde la primera deformación inelástica ocurre siempre en un contraviento, en algunos de los marcos con contraventeo en cruz, la primera deformación inelástica ocurre en una viga. A pesar de lo anterior, para ambas configuraciones de contraventeo, los mecanismos de colapso obtenidos para los modelos de baja y mediana altura (4-16 niveles) se ajustan de manera razonable al mecanismo de falla supuesto de columna fuerte-viga débil-contraviento más débil. Es importante notar que las articulaciones plásticas presentes en la base de las columnas de planta baja se deben en gran parte a la condición de empotramiento perfecto supuesta en los análisis, que es difícil de lograr en una edificación real.
Conforme se incrementa la altura de los marcos (modelos de 20 niveles), se presentan algunas fluencias en los extremos de las columnas de los niveles inferiores (Figs. 10 e, 10j , 11e y 11j ). Dichas rotaciones se desarrollan debido a la magnitud de la carga axial en las columnas exteriores, la cual es considerablemente mayor que aquélla presente en los modelos de menor altura. Se observa que la magnitud de dichas rotaciones es superior en los modelos con contraventeo en cruz respecto a las de los modelos con contraventeo chevrón; lo anterior, se debe principalmente a que los desplazamientos inelásticos globales en los marcos con contraventeo en cruz, para estás elevaciones, son superiores a los correspondientes a marcos con contraventeo chevrón, como se comenta en la sección siguiente (Fig. 12).
Los resultados de los modelos de 20 niveles con contraventeo en cruz indican el requerimiento de un ajuste en la metodología de diseño para prevenir la formación de articulaciones plásticas indeseables en las columnas de los niveles inferiores, o bien establecer un límite superior al aporte que a la resistencia a cortante deben brindar las columnas del sistema para resistir las demandas sísmicas en función de la relación de esbeltez de la estructura, tal y como se propuso para el caso de marcos con contraventeo chevrón, en que se recomienda incrementar la carga axial de diseño de las columnas de los primeros entrepisos en un 30% (Godínez 2010), pues como lo han mostrado algunos autores (Bruneau 1998, Maheri y Akbari 2003, Godínez 2010, Tapia 2011), el comportamiento y modo de falla tanto de estructuras de acero como de concreto reforzado contraventeadas es dependiente de la altura. Es importante hacer notar que dicho incremento propuesto en la carga de diseño no fue considerado inicialmente para el diseño de los marcos con contravientos en cruz, pues se deseaba valorar si dicha propuesta era aplicable también al considerar un esquema de contraventeo diferente, tal y como parece ocurrir.
Para la mayoría de los modelos de cuatro a 16 niveles con contraventeo chevrón, las diagonales en tensión no fluyen, indicando que la premisa hecha para el cálculo de la fuerza axial en las vigas, en la que se supone que las diagonales fluyen en tensión (Godínez 2010), es conservadora; sin embargo, para el caso de los marcos con contraventeo en cruz, muchas de las diagonales en tensión fluyen, por lo que en este caso la premisa parece razonable (Godínez 2012).
Los resultados expuestos en esta sección (para ambos esquemas de contraventeo), así como lo reportado por Godínez (2010 y 2012), respaldan a la disposición general de las NTCS-04 de limitar la participación de los contravientos para aportar hasta un 50% de la resistencia a cortante en marcos dúctiles, que en vista de los resultados obtenidos a la fecha, parece adecuada. Sin embargo, de lo observado para ambas configuraciones de contraventeo, los resultados son aplicables únicamente para modelos de baja y mediana altura (cuatro a 16 niveles), pues para los modelos de mayor altura (20 niveles o más) sería conveniente que el balance estipulado actualmente en las NTCS-04 varíe conforme aumenta la relación de esbeltez (H/L), como se plantea en secciones posteriores.
Capacidades de deformación globales (μ global)
A partir de las curvas cortante-distorsión idealizadas, tanto globales como de entrepiso, se obtuvieron la distorsión y el cortante asociados a la fluencia aparente para cada uno de los casos estudiados y posteriormente se calcularon las capacidades de deformación global y de entrepiso (μ = Δmax/ Δy, Fig. 5).
En la Figura 12 se muestra la variación de la capacidad de deformación global de cada modelo como función de la relación de esbeltez (H/L), tanto para los modelos con contraventeo en cruz (Fig. 12a), como para los marcos con contraventeo chevrón (Fig. 12b). En ambos casos se muestra la relación que guarda cada valor respecto al factor de comportamiento sísmico considerado en el diseño (Q=4). Se observa que la capacidad de deformación inelástica de los marcos con contraventeo en cruz es generalmente inferior respecto a los marcos con contraventeo chevrón, principalmente para los modelos de cuatro a 16 niveles; sin embargo, en los modelos de 20 niveles, en la mayoría de los casos, las ductilidades de los marcos en cruz son superiores a los chevrón.
De la Figura 12a se observa que, para los modelos con contraventeo en cruz, en ningún caso en el que el sistema de contraventeo representa la línea de defensa principal del sistema dual (modelos y25 y x25) se alcanzan ductilidades globales de cuatro, a diferencia de los modelos con contraventeo chevrón en que existen algunos modelos que sobrepasan dicho valor. De lo observado en los mapeos de rotaciones plásticas acumuladas y lo expuesto en la Figura 12, es evidente que para ambas configuraciones de contraventeo únicamente los modelos en que las columnas aportan como mínimo el 50% del cortante resistente de entrepiso son capaces de desarrollar ductilidades iguales o superiores al valor del factor de comportamiento sísmico considerado en el diseño (μglobal ≥ Q = 4), obteniendo mecanismos de colapso congruentes con el esperado. Lo anterior, principalmente ocurre en los modelos de cuatro a 16 niveles. En los modelos de 20 niveles, únicamente en los casos en que las columnas aportan aproximadamente el 75% de la resistencia a fuerza cortante de entrepiso logran alcanzarse ductilidades cercanas o iguales a cuatro. Además, al considerar este balance de resistencia se contribuye a la formación de un mecanismo de colapso más estable, reduciendo la distribución y magnitud de las rotaciones en columnas (Figs. 10, 11 y 12 )
De la Figura 12 se aprecia que existen dos parámetros de importancia en los niveles de ductilidad que ambos sistemas son capaces de desarrollar. En primera instancia, se observa que conforme la relación de esbeltez de la estructura crece, para cada balance de resistencia a cortante, las ductilidades decrecen de manera significativa. También, es claro que las ductilidades decrecen conforme aumenta el aporte de los contravientos a la resistencia a fuerza cortante de entrepiso, efecto mucho más notorio en el caso de los marcos con contraventeo en cruz (Fig. 12a). Lo anterior, indica la influencia que la altura y el balance de resistencia considerado tiene en los niveles de ductilidad que pueden desarrollar los sistemas estructurales estudiados. Esta observación sustenta nuevamente la recomendación de las NTCS-04 referente a limitar a un valor máximo del 50% el aporte del sistema de contraventeo al cortante resistente para el diseño de marcos dúctiles, independientemente del esquema de contraventeo empleado.
Efecto del esquema de contraventeo en algunos parámetros de diseño
Como se comentó, en algunos casos las capacidades de deformación global (µglobal ) son mayores que el factor de comportamiento sísmico de diseño (µglobal > Q, Figura 12). Congruente con lo realizado para marcos con contraventeo chevrón, y con la finalidad de evaluar el efecto del esquema de contraventeo en algunos parámetros de diseño, se realizaron estimaciones de dichos parámetros para una capacidad de deformación fija, en este caso la máxima permisible para el diseño de marcos dúctiles de concreto contraventeados Q = 4. Dentro de los parámetros estudiados se encuentran: 1) factores de reducción por sobrerresistencia (R), 2) distorsiones correspondientes a la fluencia (∆y ), 3) distorsiones máximas (∆max ) y, 4) distribuciones de ductilidades de entrepiso (µ). También, se hace una propuesta respecto al porcentaje mínimo de resistencia a cortante que las columnas del sistema dual deben aportar con la finalidad de fomentar un mecanismo de colapso estable. Finalmente, se propone una expresión para la estimación del periodo fundamental de vibración en base rígida independiente del esquema de contraventeo.
Todos los parámetros de diseño presentados en esta sección se estimaron con base únicamente en los resultados de los modelos en que las columnas de los marcos aportan como mínimo el 50% de la resistencia a fuerza cortante (modelos con comportamiento dúctil), pues como se comentó en las secciones precedentes, del estudio detallado de las curvas cortante-distorsión y de los mapeos de rotaciones plásticas acumuladas, se observó, que el comportamiento de los modelos en que las columnas aportan un porcentaje menor al 50% de la resistencia a fuerza cortante (modelos y25 y x25) no es satisfactorio para el diseño de sistemas dúctiles para ninguno de los dos esquemas de contraventeo estudiados.
Factores de reducción por sobrerresistencia (R)
Con base en las curvas cortante-distorsión ajustadas de los modelos con contraventeo en cruz, se calcularon los factores de reducción por sobrerresistencia (R=Vu/Vdis , Figura 5), para su posterior comparativa con los valores correspondientes a marcos con contraventeo chevrón.
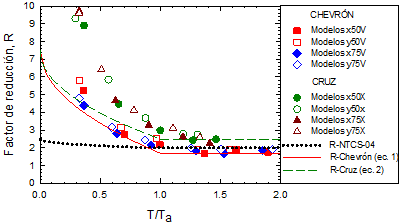
En la Figura 13 se muestra la variación de los factores R respecto al valor T/Ta . Como se observa, los factores R muestran dependencia con el esquema de contraventeo, pues para el intervalo de periodos estudiado, los valores de R calculados para marcos con contraventeo en cruz son mayores que los calculados para marcos con contraventeo chevrón. Por lo tanto, se proponen expresiones independientes para la determinación de los factores R al considerar sistemas duales con contravientos metálicos tipo chevrón y en cruz (Ecs. 1 y 2, respectivamente). Es importante aclarar que la expresión inicialmente propuesta por Godínez (2010) para el cálculo de los factores R en sistemas con contraventeo chevrón fue modificada con la finalidad de obtener un mejor ajuste a los valores teóricos. Las ecuaciones propuestas tienen la forma general con la cual se determinan los factores de reducción por sobrerresistencia en la nueva propuesta del Manual de Obras Civiles de la Comisión Federal de Electricidad (MOC-2008 2009 y Tena et al. 2009), que podría ser adoptada en futuras versiones del Reglamento de Construcciones del Distrito Federal. Siguiendo dicho enfoque, se tendrían valores de R0 = 1.7 y R1 = 5.8 para marcos con contraventeo chevrón, y valores de R0 = 2.5 y R1 = 5.0 para marcos con contraventeo en cruz.
En la Figura 13 se muestran los valores con base en los cuales se derivaron las Ecuaciones 1 y 2, así como las curvas descritas por cada una de ellas, además de una curva que define la propuesta actual del Apéndice A (AA) de las NTCS-04. Como se observa, ambas propuestas son conservadoras, pues en la mayoría de los casos, las curvas propuestas se encuentran por debajo de los valores teóricos. Al comparar las curvas propuestas con la correspondiente de las NTCS-04, se observa que en ambos casos se presentan valores superiores a los especificados en el AA para la zona de periodos cortos; en tanto que para la zona de periodos largos, para el caso de marcos con contraventeo en cruz, se proponen valores mayores a los actualmente considerados en las NTCS-04, y para marcos con contraventeo chevrón, se proponen valores inferiores. Con lo anterior se obtienen valores más cercanos a los calculados teóricamente. Las expresiones propuestas están sustentadas en evidencia analítica desarrollada específicamente para el sistema estructural considerado, a diferencia de la propuesta actual de las NTCS-04, la cual se basa en los valores obtenidos de modelos de marcos momento-resistentes de concreto reforzado (Tena 2008).
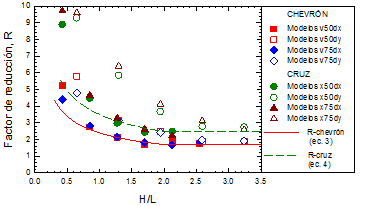
De forma complementaria, en la Figura 14 se presenta la relación entre los factores de reducción por sobrerresistencia (R) y la relación de esbeltez (H/L); así como las Ecuaciones 3 (para marcos chevrón) y 4 (para marcos en cruz) que pueden ser útiles para realizar una estimación rápida de los factores R esperados en función de la relación de esbeltez de la estructura. Es importante hacer notar que las estimaciones realizadas con las Ecs. 3 y 4 difieren de las obtenidas con base en las Ecs. 1 y 2 y son válidas para relaciones de esbeltez 0.4≤H/L≤4. Sin embargo, las Ecs. 3 y 4 pueden dar una idea razonable de los factores R como función exclusiva de la geometría de la estructura, por lo que se consideran de ayuda.
De las Figuras 13 y 14 se observa que, para ambos esquemas de contraventeo, los factores de reducción por sobrerresistencia decrecen de manera significativa conforme se incrementa la relación de esbeltez y el periodo de la estructura. Se observa también, que para las estructuras más rígidas, conforme se incrementa el porcentaje de fuerza cortante que resisten las columnas, decrecen los valores de R.
El criterio empleado para el planteamiento de las Ecuaciones 1 y 2 se basa en procurar que las curvas descritas por dichas ecuaciones se encuentren lo más cercano posible a los valores teóricos mínimos calculados para cada periodo o relación T/Ta. Dado el criterio adoptado, es claro que para aquéllos casos en que para un mismo valor de T/Ta existen varios valores de R, las estimaciones realizadas mediante las Ecs. 1 y 2 ajustarán de muy buena forma a los valores analíticos inferiores, y la diferencia se incrementará conforme dichos valores teóricos se alejen del valor mínimo. Sin embargo, se procuró que en todos los casos las estimaciones realizadas no fueran inferiores al 75% de cada valor teórico calculado. Con lo anterior se obtienen valores menos conservadores que los actualmente propuestos en las NTCS-04, además de estar basados en resultados analíticos específicos al sistema estructural reportado. Se empleó el mismo criterio para la definición de las Ecuaciones 3 y 4.
Distorsiones asociada al estado límite de servicio (Δy)
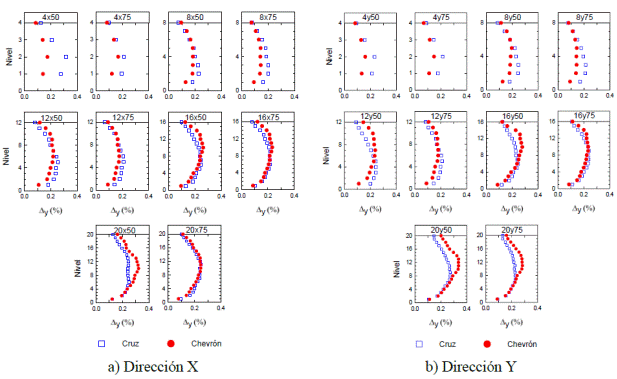
En la Figura 15 se presentan las envolventes de distorsiones asociadas a la fluencia de cada entrepiso, para las dos direcciones de análisis y ambas configuraciones de contraventeo, las cuales se estimaron con base en las curvas bilineales idealizadas de las curvas cortante-distorsión reales (Figura 5). La importancia de dichas envolventes radica en que en algunos códigos de diseño sísmico se emplea esta estrategia simple para la definición de parámetros de diseño (Tena 2008).
Idéntico a lo observado en marcos con contraventeo chevrón (Godínez 2010), en los marcos con contraventeo en cruz, las distorsiones de fluencia son menores a la estipulada como distorsión límite de servicio en el Apéndice A de las NTCS-04 (Δser=0.004). Lo anterior se debe a que este límite se basa en estudios de marcos momento-resistentes, mostrando la necesidad de definir valores específicos a los sistemas estructurales en estudio.
Con la finalidad de proponer una distorsión de fluencia límite para sistemas con base en marcos de concreto reforzado con contraventeo chevrón, Godínez (2010) calculó el promedio de las distorsiones de fluencia de cada uno de los entrepisos que presentaron comportamiento inelástico. Para valorar si dicha propuesta es aplicable a marcos con contraventeo en cruz, se empleó el mismo criterio para el cálculo del promedio de las distorsiones de fluencia de cada uno de los entrepisos que presentaron comportamiento inelástico. Los resultados expuestos en la Figura 16, para ambas configuraciones de contraventeo, se presentan contra el periodo natural (T) normalizado respecto al número de niveles de cada modelo en consideración (N), el cual representa un parámetro simple de la rigidez. En la Figura 16 se indican la desviación estándar y el coeficiente de variación asociado a cada esquema de contraventeo.

Figura 16 Propuesta para la definición de la distorsión de fluencia asociada al estado límite de servicio
Debido a la condición de frontera considerada (empotramiento en la base de las columnas), no se incluyeron las distorsiones de entrepiso del primer nivel en el cálculo de la distorsión promedio.
Con base en los cálculos realizados para marcos con contraventeo en cruz, se concluye que la distorsión de fluencia promedio propuesta previamente para marcos con contraventeo chevrón (Δy=0.002, Godínez 2010), la cual se expresa mediante una línea recta horizontal en la Figura 16, es adecuada para ambas configuraciones de contraventeo. Por lo tanto, la distorsión de fluencia puede considerarse como independiente del esquema de contraventeo.
La distorsión media de fluencia propuesta (Δy=0.002) puede tomarse en cuenta para el diseño de sistemas duales con base en marcos de concreto reforzado con contraventeo metálico al realizar la revisión asociada al estado límite de servicio, ya que el límite propuesto toma en cuenta la rigidez específica (masa y/o periodo) de los sistemas estudiados, aspecto que no se toma en cuenta en la propuesta actual del AA de las NTCS-04.
Distorsión asociada al estado límite de prevención de colapso (Δmax)
En la Figura 17 se muestran las envolventes de distorsiones máximas para ambas configuraciones de contraventeo y ambas direcciones de análisis. Estas curvas brindan una idea razonable de la distorsión máxima que estos sistemas pueden desarrollar con fines de diseño. Con la finalidad de verificar si la distorsión máxima de diseño propuesta en las NTCS-04 para el sistema estructural en estudio resulta adecuada, se calcularon los promedios de las distorsiones de los entrepisos de los marcos en que se presentan los desplazamientos máximos (Fig. 18) respecto a la relación de esbeltez (H/L). De los promedios de distorsiones máximas y las envolventes máximas de distorsiones de entrepiso (Figs. 17 y 18 ), se puede concluir que el límite de distorsión asociado a la revisión del estado límite de colapso actualmente propuesto en las NTCS-04, así como en el ASCE 7-10 (Δmax=0.015), cubre de forma adecuada las demandas de distorsión observadas en todos los modelos.
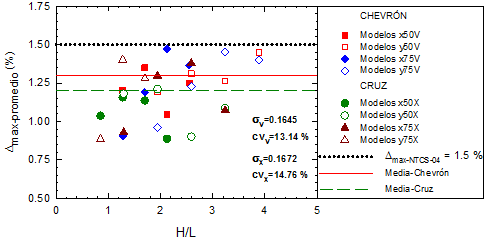
Figura 18 Revisión de la distorsión asociada al estado límite de seguridad contra colapso de las NTCS-04
Es importante aclarar que, las envolventes de distorsiones máximas expuestas, inicialmente calculadas por Godínez-Domínguez y Tena-Colunga (2010) y Godínez y Tena (2011), para el caso de marcos con contraventeo chevrón, se obtuvieron con la finalidad de proponer una distorsión máxima de diseño para el sistema estructural en estudio, empleando el mismo criterio que en la definición de la distorsión asociada al estado límite de servicio. Para lo anterior, se obtuvo el promedio de las distorsiones máximas de los entrepisos de los marcos en que se presentaban los desplazamientos máximos. Con base en los resultados obtenidos, se propuso una distorsión máxima de diseño (asociada al estado límite de colapso) igual a Δmax = 0.013, la cual, como se comentó, representa el promedio de las distorsiones consideradas. En Godínez y Tena (2011) se hizo notar que el valor propuesto para la revisión del estado límite de colapso (Δmax = 0.013, Fig. 18) es inferior al valor actualmente establecido en algunos códigos internacionales (por ejemplo ASCE 7-10, 2010) y en el Apéndice A de las NTCS-04, por lo que posteriormente en Godínez y Tena (2012), y Godínez-Domínguez y Tena-Colunga (2012), se realizaron análisis dinámicos no lineales paso a paso de modelos de edificios con contraventeo chevrón de 8, 15 y 24 niveles, en los que se obtuvieron las envolventes máximas y promedio de distorsiones de entrepiso dinámicas. Con base en dichos resultados fue posible concluir que el límite de distorsión asociado a la revisión del estado límite de colapso actualmente propuesto en las NTCS-04, así como en el ASCE 7-10 (2010), cubre de mejor manera las demandas de distorsión observadas, que el límite propuesto en la primera parte de la investigación con base en los análisis estáticos no lineales.
Por lo comentado, en este estudio, se procedió de la misma manera que en Godínez-Domínguez y Tena-Colunga (2010) y Godínez y Tena (2011) para el caso de marcos chevrón, aunque en este caso se omitió el cálculo del valor promedio, centrando la atención en verificar que, tal y como ocurrió en los estudios previamente citados, el límite de distorsión asociado a la revisión del estado límite de colapso actualmente propuesto en las NTCS-04, así como en el ASCE 7-10 (Δmax=0.015), cubre de forma adecuada las demandas de distorsión observadas en todos los modelos. Debe notarse que el valor promedio obtenido de los marcos en cruz es muy parecido al obtenido para marcos chevrón (Δmax=0.012, Fig. 18). El conjunto de resultados citado respalda con evidencia numérica el límite establecido en las NTCS-04 para la revisión de la distorsión asociada al estado límite de prevención de colapso.
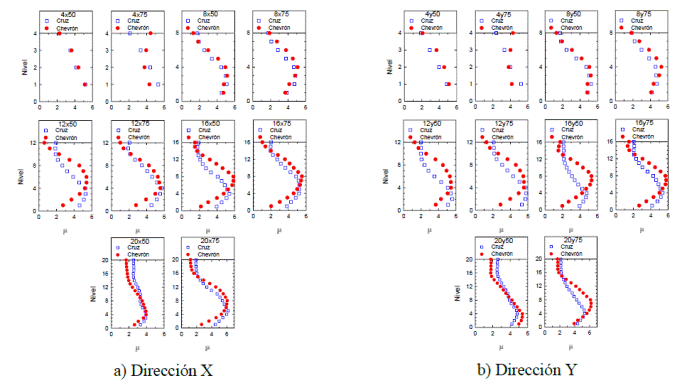
Capacidad de deformación inelástica (ductilidades de entrepiso, μ)
En la Figura 19 se muestran las ductilidades de entrepiso para ambas configuraciones de contraventeo y ambas direcciones de análisis. Por simplicidad, aquellos entrepisos donde la respuesta es elástica se identifican mediante μ=1. Se observa que para la mayoría de los modelos las capacidades de deformación no son uniformes. La distribución de ductilidades en elevación de los modelos de cuatro y ocho niveles es muy similar para ambas configuraciones de contraventeo. Para los modelos de cuatro a 16 niveles con contraventeo chevrón, las mayores capacidades de deformación se localizan en los entrepisos intermedios (entrepisos 2 a 4 en los modelos de ocho niveles y entrepisos 3 a 5 en los modelos de 12 niveles). Sin embargo, para los marcos con contraventeo en cruz, los máximos se localizan en los entrepisos ubicados en el primer tercio de la altura, principalmente para los modelos en que las columnas aportan aproximadamente el 50% del cortante resistente. Para los modelos de 20 niveles, en ambos casos, las mayores capacidades de deformación se localizan en los entrepisos ubicados en el primer tercio de la altura (entrepisos 6 a 8). Como se ha observado también en otros sistemas estructurales (por ejemplo, marcos momento-resistentes), la capacidad de deformación decrece en los entrepisos superiores, encontrando en varios casos comportamiento muy cercano al elástico.
Se observa nuevamente, para ambos esquemas de contraventeo, que la capacidad de deformación inelástica decrece conforme se incrementa la contribución del sistema de contraventeo en la resistencia a fuerza cortante de entrepiso.
Estimación del aporte mínimo de las columnas al cortante resistente del sistema ante carga lateral
En esta sección se propone una ecuación en función de la relación de esbeltez de la estructura (H/L) para la estimación del porcentaje mínimo de resistencia a fuerza cortante que las columnas de un entrepiso deben aportar en los sistemas duales (Ecuación 5). La expresión propuesta se basa en el estudio de los mecanismos de colapso y los balances de resistencia para los que fueron diseñados tanto los marcos chevrón como los marcos en cruz (Fig. 20).

Figura 20 Propuesta para la determinación del aporte mínimo de las columnas al cortante del sistema resistente ante carga lateral, en porcentaje.
En la propuesta de la Ec. 5 se toma en cuenta que conforme se incrementa la relación de esbeltez de las estructuras (H/L), es importante tratar de limitar la contribución del sistema de contraventeo al cortante resistente, evitando con esto la transmisión de cargas axiales muy elevadas a las columnas de soporte, pues aunado a las altas cargas axiales derivadas de las fuerzas sísmicas, la ductilidad de curvatura de las secciones de columnas podrían reducirse significativamente, impactando directamente en la capacidad de deformación global que el sistema estructural puede desarrollar. Por lo anterior, la curva descrita por la Ec. 5 fue propuesta de tal manera que, para las estructuras esbeltas (2.5≤H/L≤4), se cubran la mayoría de los puntos correspondientes a los modelos en que las columnas aportan aproximadamente el 75% de la resistencia a cortante, pues fue para este balance de resistencia donde se observó un mejor comportamiento estructural. Sin embargo, el criterio empleado para la definición de la curva para las estructuras menos esbeltas (0.5≤H/L<2.5), toma en cuenta lo comentado previamente, en que de los mapeos de rotaciones plásticas acumuladas se observaron comportamientos muy similares en los modelos en que las columnas aportan tanto el 50% como el 75% al cortante resistente (indicados respectivamente mediante círculos y cuadrados en la Figura 20), por lo que en esta zona se consideró que el aporte mínimo de las columnas al cortante resistente de entrepiso puede ser menor que en el caso de estructuras esbeltas. Así la curva propuesta trata de cubrir a todos los datos indicados mediante círculos, sin que sea necesario cubrir aquéllos valores correspondientes a los modelos en que teóricamente las columnas aportan un mayor porcentaje de fuerza cortante. Finalmente, en la zona en que H/L<0.5, en dónde se encuentran los modelos más rígidos, cuyos diseños pueden estar regidos de forma importante por las combinaciones de cargas verticales, se decidió adoptar la propuesta de las NTCS-04, en que el aporte mínimo de las columnas corresponde a un 50%, valor con el que se observó un comportamiento estructural satisfactorio.
La Ecuación 5 es aplicable a ambos esquemas de contraventeo y demanda un mayor aporte de las columnas al cortante resistente que en la propuesta inicial (Ec. 6), en que se consideran exclusivamente los resultados de los marcos chevrón (Godínez 2010), pues como se ha observado, conforme mayor sea el aporte de las columnas al cortante resistente de entrepiso, las distribución y magnitud de las rotaciones en columnas decrece, así como la ductilidad del sistema dual se incrementa, aspecto deseable. Con lo anterior, se busca que los mecanismos de colapso obtenidos sean congruentes con la filosofía de diseño, es decir, columnas fuerte-viga débil-contraviento más débil. La Ecuación 5 es válida para relaciones de esbeltez 0.4≤H/L≤4 (0.203≤T≤1.774), intervalo en que se encuentran los marcos estudiados y para los cortantes basales de diseño de la zona III-b considerando un factor de comportamiento sísmico Q = 4.
donde:
VRCol = Aportación mínima de las columnas de un entrepiso al cortante resistente, en porcentaje.
H = Altura total del edificio.
L = Longitud de la base de la estructura en el sentido de análisis.
En la Figura 20 se presentan la curvas descritas por la nueva ecuación propuesta (Ec. 5), y la previamente derivada para marcos chevrón (Ec. 6, Godínez 2010). Debe notarse que en la propuesta realizada únicamente se consideraron los resultados de los modelos en que las columnas aportan como mínimo el 50% de la resistencia a cortante de entrepiso.
Como se comenta en Godínez y Tena (2011), debe considerarse que la propuesta anterior por sí misma no es suficiente para obtener mecanismos de colapso consistentes con los esperados, dado que el comportamiento inelástico del sistema estructural en estudio (como de cualquier otro) está influenciado por diferentes parámetros, como la capacidad de deformación de las vigas, los niveles de carga axial en las columnas (que limitan su capacidad de deformación), la relación de esbeltez empleada en las diagonales de contraventeo (que impactan su modo de falla en pandeo), las condiciones de compacidad y el grado del acero, así como la configuración seleccionada para realizar las conexiones. Sin embargo, éste puede considerarse como un buen punto de partida para ayudar en lo posible a la formación de mecanismos de colapso consistentes con los estipulados en las premisas de diseño para marcos de concreto reforzado contraventeados.
Propuesta para la estimación del periodo fundamental
Se proponen a continuación expresiones para la estimación del periodo fundamental en base rígida. En primera instancia se obtuvo una ecuación considerando exclusivamente los datos correspondientes a marcos con contraventeo en cruz y se comparó con la previamente propuesta para marcos con contraventeo chevrón. Debido a que ambas expresiones conducen a estimaciones semejantes, se propone una expresión única realizando un ajuste lineal para el universo de los datos.
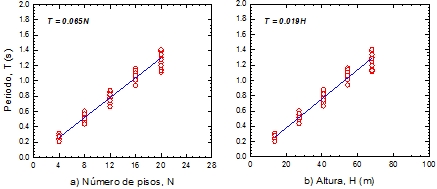
En las Figuras 21a y 21b se muestra la tendencia de los periodos de vibrar conforme se incrementa tanto el número de niveles, como la altura de los marcos. Como se observa, una relación lineal representa de manera razonable y simple el comportamiento obtenido en ambos casos. Con base en esto, se proponen dos expresiones (Ecuaciones 7 y 8) para la estimación de los periodos de vibrar en base rígida de sistemas duales con base en marcos de concreto reforzado con contraventeo metálico en función del número de niveles (N) y la altura (H), respectivamente. Las ecuaciones propuestas se representan en las Figuras 21a y 21b mediante una línea recta. Como era de esperarse, debido a la rigidez de este tipo de estructuras, los periodos calculados con base en las ecuaciones propuestas son menores que los calculados con base en expresiones similares (Murià y González 1995) para el caso de estructuras con base en marcos momento-resistentes. Las expresiones propuestas brindan aproximaciones razonables respecto a los valores obtenidos en modelos tridimensionales de diferentes alturas (Godínez et al. 2012, López y Aparicio 2014)
donde:
T = Periodo fundamental de vibración en base rígida
N = Número de pisos del edificio
H = Altura total del edificio (en metros)
Conclusiones y comentarios finales
Se presentó un estudio en que se evalúa, mediante análisis estáticos no lineales ante carga monótona creciente, la influencia del esquema de contraventeo en algunos parámetros de diseño específicos. Asimismo, se evalúa el comportamiento de marcos dúctiles de concreto reforzado con contraventeo metálico en cruz de entre cuatro y 20 niveles ubicados en la zona del lago del Distrito Federal. De los resultados expuestos, se pueden hacer los siguientes comentarios y observaciones:
(1) El empleo conjunto de la metodología de diseño por capacidad previamente planteada para el diseño de marcos con contraventeo chevrón, haciendo las adaptaciones necesarias para considerar el cambio en el esquema de contraventeo, y el uso de algunas recomendaciones actualmente establecidas en los códigos de diseño, permite realizar diseños dúctiles de estructuras nuevas con base en marcos de concreto reforzado con contraventeo en cruz. La metodología de diseño empleada sigue un proceso secuencial de acuerdo al mecanismo de falla esperado, es decir, en primera instancia debe diseñarse la rigidez y resistencia del sistema de contraventeo, posteriormente las vigas, y finalmente debe realizarse el diseño de las columnas y las conexiones para revisar la integridad de los nudos.
(2) Si se emplea una metodología de diseño por capacidad conforme a lo indicado en el punto anterior, es factible obtener mecanismos de colapso cercanos al supuesto de columna fuerte - viga débil - contraviento más débil, y capacidades de deformación y de sobrerresistencia razonables para los modelos de baja y mediana altura (cuatro a 16 niveles) cuando las columnas de los marcos con contraventeo en cruz contribuyen por lo menos con el 50% de la resistencia a fuerza cortante del entrepiso. Estos resultados, y los previamente obtenidos para marcos con contraventeo chevrón, respaldan a la disposición general de las NTCS-04 de limitar la participación de los contravientos para aportar hasta un 50% de la resistencia a cortante en marcos dúctiles.
(3) Para ambas configuraciones de contraventeo, se observa una relación entre los factores de reducción por sobrerresistencia (R) calculados y el porcentaje que las columnas aportan al cortante resistente. A medida que dicho porcentaje se incrementa, los factores R disminuyen.
(4) Existe dependencia de los factores de reducción por sobrerresistencia (R) con el esquema de contraventeo considerado, por tal razón, se proponen dos nuevas expresiones para el cálculo de los factores R, tanto para marcos con contraventeo en cruz como para marcos con contraventeo chevrón.
(5) La distorsión asociada a la fluencia para la revisión del estado límite de servicio, es independiente del esquema de contraventeo, corroborando que la distorsión de fluencia propuesta previamente para marcos con contraventeo chevrón (Δ y = 0.002 ), es también aplicable para marcos con contraventeo en cruz.
(6) Se verificó que la distorsión máxima de diseño empleada para la revisión del estado límite de prevención de colapso, actualmente recomendada en algunos códigos internacionales y en el Apéndice A de las NTCS-04 (Δmax = 0.015), cubre de forma segura las envolventes de distorsiones máximas para ambas configuraciones de contraventeo.
(7) Para los modelos de mayor altura (20 niveles o más) es necesario un ajuste en la metodología de diseño para prevenir la formación de articulaciones plásticas indeseables en las columnas de los niveles inferiores. Una estrategia sugerida para evitar esto es establecer un límite superior en el porcentaje de resistencia a fuerza cortante mínimo que las columnas de un entrepiso deben aportar para resistir las demandas sísmicas en función de la relación de esbeltez de la estructura, a diferencia de lo actualmente estipulado en las NTCS-04 en que se considera un límite constante en altura. Una estrategia adicional, que requiere de estudios detallados, radica en incrementar en 30% la carga axial de diseño de las columnas de esquina y de borde de los niveles inferiores en el caso de estructuras esbeltas (H/L>2.5), tal y como se propuso para el caso de marcos con contraventeo tipo chevrón.
(8) Con lo finalidad de obtener mecanismos de colapso congruentes con la filosofía de diseño, se propone una nueva expresión para la estimación del porcentaje de resistencia a fuerza cortante mínimo que las columnas deben aportar a la resistencia total en función de la relación de esbeltez de la estructura (H/L), la cual difiere de la propuesta previamente realizada para marcos chevrón.
(9) Se proponen dos expresiones simples para la estimación de los periodos fundamentales de vibrar de estructuras con base en marcos de concreto reforzado con contravientos metálicos (chevrón o en cruz) en base rígida, en función del número de niveles de la estructura o, en su caso, en función de la altura de la misma. Las expresiones propuestas brindan aproximaciones razonables respecto a los valores obtenidos en modelos tridimensionales de diferentes alturas .
Las recomendaciones derivadas de este estudio tratan de fomentar el diseño de estructuras que presenten un comportamiento estructural congruente con la filosofía de diseño ante excitaciones sísmicas intensas; es decir, fomentar comportamientos estructurales que conduzcan a mecanismos de colapso de columna fuerte-viga débil-contraviento más débil. Por lo tanto, las propuestas realizadas pueden emplearse para estructuras diseñadas en zonas del valle de México distintas a la considerada en el estudio, siempre y cuando se tengan en consideración las características geométricas y los factores de comportamiento sísmico empleados en el desarrollo de esta investigación (estructuras regulares diseñadas con Q=4).
Agradecimientos
El autor agradece el apoyo de Conacyt para la elaboración de este proyecto, el cual se realizó dentro del marco del programa de Apoyos Complementarios para la Consolidación Institucional de Grupos de Investigación (Repatriación, Retención y Estancias de consolidación) 2010. Se agradecen ampliamente los comentarios y sugerencias de los revisores anónimos, los cuales ayudaron a mejorar la calidad de este artículo. También, se agradece ampliamente al Dr. Arturo Tena Colunga por los comentarios y el interés en el trabajo aquí presentado.











 nueva página del texto (beta)
nueva página del texto (beta)