PACS: 83.60.Bc; 83.80.Gv; 47.65.Cb; 66.10.cg; 83.60.Df
1. Introduction
Ferrofluids are colloidal suspensions of permanently magnetized particles of nanometer size dispersed in a solvent. Their rheological properties such as viscosities, storage of energy and dissipative moduli can be controlled with external magnetic fields 1, which makes them valuable in diverse technological applications. Much of the research on these magnetic fluids relates to the class of magnetorheological suspensions which develop bulk magnetization under external magnetic field conditions 2. External fields produce chain-like aggregates of the colloidal particles, an effect that can also be developed in ferrofluids in the absence of fields for sufficiently high particle’s dipolar moment or concentration. It has been observed that when the fluid is subjected to an applied increasing shear rate they change from their Non-Newtonian (nonlinear relationship of stress with the applied shear flow, which it can be produced by thermal fluctuations too) to Newtonian (the stress response of the liquid is linear through a kernel with the shear rate. With the kernel been the stress relaxation modulus) under magnetic fields. Such rheological behavior has been demonstrated to be anisotropic through the use of macroscopic rheology experiments 3, and also more recently through a no invasive technique, the passive microrheology on a probe particle diffusing in the colloidal suspension 4 in thermal equilibrium. In their development of this latter experimental technique by Mason et al5, they express “bulk relaxations have the same spectrum as the microscopic stress relaxations affecting the suspended particle motion". They assumed that the complex shear moduli can be determined from the particle’s mean squared displacement in the linear regime of low shear flow. This technique has a significant sensitivity and detects high frequencies of relaxations as compared to macroscopic rheology. Ferrofluids look dark with visible light because of its strong absorption by the ferro-colloids. Mertelj et al.4 were able to measure the translational diffusion of the probe particle with their use of low-intensity laser beams in dynamic light scattering experiments. In their research, they used small samples which together a careful selection of wavelengths allowed them to reduce the absorption of light by the ferrocolloids. Whereas Yendeti et al6 made their microrheology experiments observing a fluorescence silica colloidal particles suspended in the ferrofluid. This way they were able to use video microscopy to track the silica particle positions driven by its Brownian motion inside the ferrofluid. Thus, fine tuning of the wavelength to the order of the probe particle size allows the determination of its mean squared displacement. Therefore, the scattered light originates only from the probe silica colloidal particle since the molecules of the solvent are much smaller than the wavelength of the used light. Solvent provides the reservoir that dissipates energy from the translational and rotational movement imparted by the Brownian motion of all the colloidal particles. It was shown in Refs. 7 and 8 that dynamic light scattering and video microscopy in microrheology experiments allows the determination of the orientation variable, thus, providing the rotational diffusion of the probe. From its angular displacements, the time-dependent mean squared angular displacement was measured. Consequently, the microrheological shear modulus of the host suspension was obtained. Comprehensive theoretical knowledge of the main measured rheological properties have been reached with thermodynamic 9,10,11,12,13,14,15, and kinetic theories of liquid crystal dynamics 16 that involve macroscopic constitutive magnetization’s relaxation mechanisms, and both mean field and microscopic free energies of the thermodynamic state, respectively. Thus, the experimentally observed dependence of viscosity with magnetic field was accurately confirmed with a kinetic approach from low up to moderate concentrations before the formation of chain structures by the particles 17. After the formation of chains, a so-called kinetic chain theory of rod-like aggregates 18,19 confirms the observations on the increase of viscosity with field quantitatively. In a similar set of macroscopic experiments at low strain in a system where the finite size of the vessel containing the liquid was important 20, it was determined the energy dissipated due to aggregate’s structural deformation when they are partially bound to the confining walls. It was found that the aggregates experience cohesion and movement of their inner constituting particles which generates heat through this process. Such a heating mechanism is relevant in hyperthermia applications where ferro-particles diffuse, rotate and stick to the boundaries in the multicomponent medium inside of a tissue 21. These findings have raised the interest to investigate the rheology of complex fluids of mixtures of added polymer solutions to the magnetorheological fluid 20,22,23,24. Thus, the theoretical description of their observed rheology and effect of size polydispersity 25,26,27,28, have been described with polymers motivated models 29,30. More recently, theories based on macroscopic thermodynamics predict as in polymer theory elongational viscosity and its consequence on the ratios of the viscoelastic moduli 30, and of the module to viscous dissipation time. Such predictions were adopted in the microrheology experiments of Refs. 4,6 in order to get estimates for the values of all anisotropic properties. In the present manuscript we propose expressions for the complex shear modulus response for the rheology of an equilibrium ferrofluid derived from a statistical mechanics approach valid in the regime of linear shear flow of microrheology experiments. The viscoelastic moduli depend on the pair distribution function which captures the bulk microstructure of the ferro-particles due to their pair direct interactions. We show that for a given concentration of particles, ferrofluids at equilibrium state display rheological behavior in a similar way as it is observed to occur in non-equilibrium anisotropic magnetic fluids under external fields and shear flow. For the dispersed homogeneous phase of the colloid, we found that the dissipative modulus is dominant at low frequencies where the colloid displays a liquid character with a crossover to an elastic fluid mode at moderate frequencies where the elastic modulus becomes dominant at higher frequencies. The calculated loss modulus has good agreement with Langevin dynamic simulations up to the transition to the elastic behavior where it starts to deviate. Whereas the general shape of the elastic modulus, as obtained from simulations of the mean square translational displacement of a probe ferro-particle is qualitatively well described by the model proposed. An increase of the dipolar moment per particle or of their concentration can lead to the formation of chain like aggregates in absence of external fields. Our model theory of microrheology is useful in this case too. Since the formation of chains is taken into account properly by the pair correlation function which describes the bulk micro-structural order of the particles due to their direct interactions. We also provide the analytical expressions for these moduli when the observable is the mean square angular rotation for experiments that observe the rotational diffusion of ferro-particles. These viscoelastic properties can also be used to study in the linear regime of flow the rheology of equilibrium isotropic ferroelectric colloids 31,32,33.
2. Translational diffusion microrheology
Tracking microrheology experiments are useful techniques that accurately provide the
linear viscoelasticity of suspensions of polystyrene particles and other complex
fluids 5,7,34,35. In these experiments it is assumed that the complex
shear moduli can be determined from the particle’s mean squared displacement in the
linear regime of low shear flow. The rheological properties are extracted through
the equilibrium Einstein expression of the friction on a probe particle that
performs a Brownian motion in the colloid. The friction due to interaction with its
neighbors, in the frequency space
with
The Langevin equations of the translational and rotational Brownian motion of the probe particle that interacts with the others in the suspension are the stochastic Eqs. 36
V(t) and W(t) are the translational and angular
velocities of the probe. We used a space fixed frame with origin at the particle
center of mass, and frame axis following the orientation of the probe main axis of
symmetry. M and I are the mass and particle’s matrix of moment of inertia,
respectively. We shall not consider neither hydrodynamic interactions among
particles nor external magnetic fields. The first two terms in Eqs. (2) are the
solvent friction force and torque. The short time free particle diagonal friction
tensors
and kB Boltzmann constant, T =
300K the absolute temperature. The total force
FTOT and torque
TTOT on the probe by the other
colloidal particles which are at the concentration
with
Both Langevin equations can be written compactly as
where
where
with
The diffusion relaxation of the host particles around the probe is provided by
which has initial condition
which determines the relaxation modes of the cage of particles surrounding the probe.
Its initial condition
Substituting the above solution for
where
is a fluctuating generalized force arising from the spontaneous departures from zero
of the net direct forces exerted by the other particles on the tracer. It groups a
random force and torque on the tracer with zero mean value, and time dependent
correlation function given by
Using the Wertheim-Lovett’s relation 38
we derive other useful forms of the friction function
with
The time-dependent memory function
This is a general expression for the friction contribution on the tracer due to
direct interactions with the particles about it. It depends on the microstructural
inhomogeneous total correlation function
Using the above approximation for
This last equation governs the diffusive relaxation of C(t),
as described from the tracer’s reference frame. In this manner, we have obtained a
closed approximate expression for
From (15) the 6x6 diagonal friction matrix, where it is ignored translational and rotational coupling is
with
Thus, the friction matrix (17) has only five non zero diagonal elements;
The colloidal ferrofluid is contained in a volume V. It consist of a
carrier fluid which molecular nature is not taken into account, plus the
monodisperse system of N spherical particles where each one has a permanent dipolar
moment
with
with
with the identification
By taking the Fourier-Bessel
42 with jl being the spherical Bessel function, and Laplace transform
of (16) (See Ref. 36) we find
where
42. Using the above values of
mnl = 000, 110, 112, then for dipolar liquids
And the inverse relation holds 42
Thus
The structure factor
Using the invariant spherical harmonic expansion in Eq. (17) we obtain the friction function on the probe (tracer) particle
with the single time dependent relaxation function
3. Microrheology under linear shear flow and no external magnetic field
We assume now that the viscoelastic response of the ferrofluid to variations of
strain rate
with shear relaxation modulus G(t). Because the
shear stress divided by the shear rate has dimensions of viscosity, it is defined
the complex viscosity
where
we find
Because for dipolar particles
The complex viscosity of a viscoelastic fluid is defined as
The normalized frequency
and the dissipative modulus
with
where we introduced the auxiliary definitions
The imaginary part is
Given the known material values of
The Fourier-Bessel transform of the projections of the total correlation function
In Lammps simulations we used dimensionless units for, the particle energy at room
temperature, length and mass which were obtained with respect to those of the
ferrofluid Fe2O3, given by
the values 2;
Figure 1 is a log-log plot that depicts the
behavior of

Figure 1. The viscoelastic model of Eqs. (5-8) has three characteristic
relaxation times
4. Viscoelastic moduli
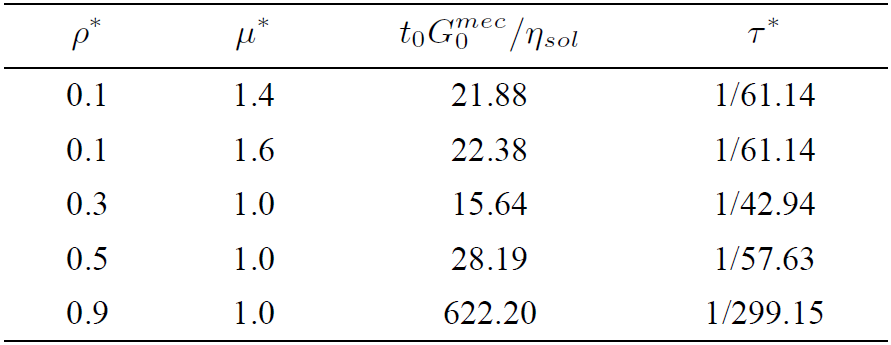
In Fig. 2 are plotted in log-log scale the
elastic G´(w) and dissipative
G”(w) modulus versus frequency at three
reduced densities
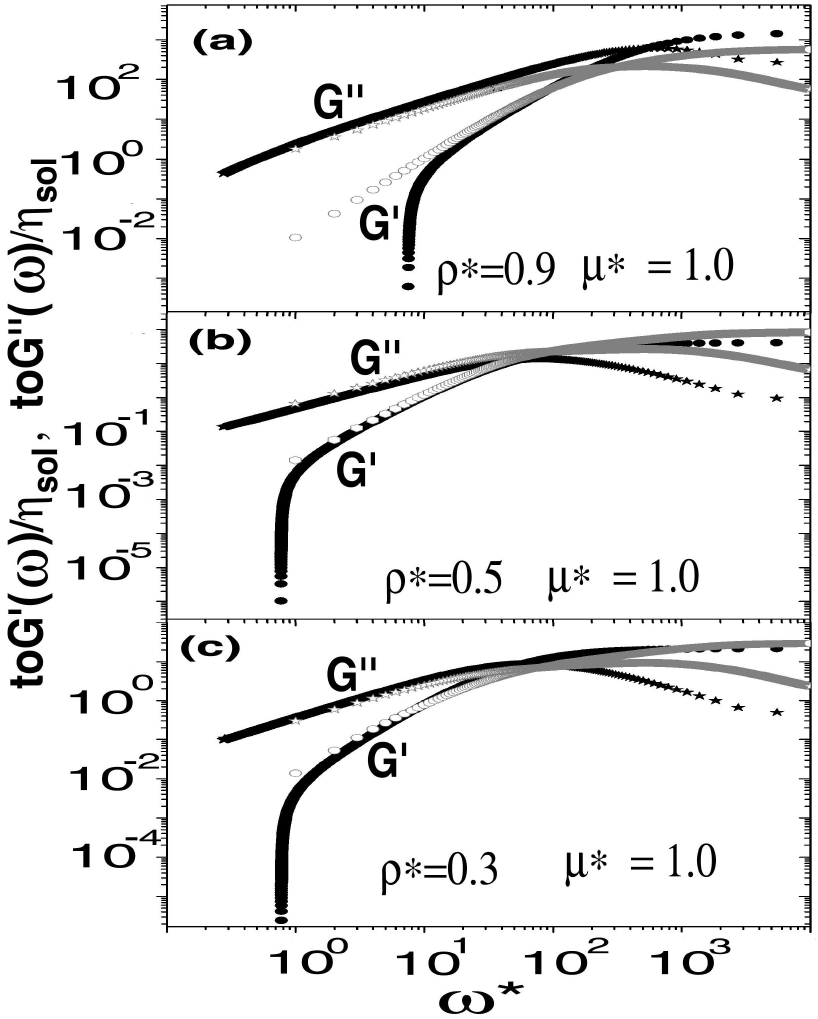
Figure 2. Logarithmic plot of elastic G' and loss
G'' moduli versus logarithm of dimensionless
frequency
Our derived expressions of Eqs. (35-37) have the same frequency dependence as a
continuous mechanical (mec) model of Maxwell viscoelasticity given by 45
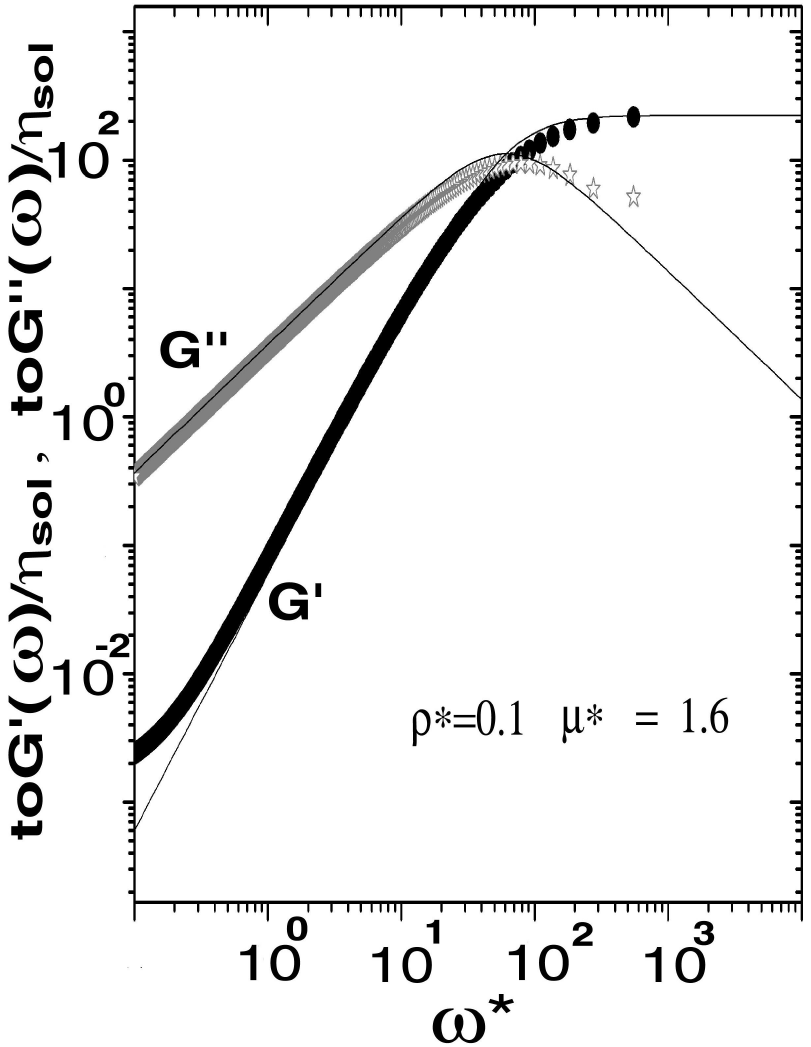
Figure 3. Brownian dynamic simulations of viscoelastic moduli as a function of
frequency for a fixed concentration and dipolar moment. Simulation
calculation of G' is denoted with
The value of
At longtimes, the self-diffusion of a particle is
Our results for viscoelastic moduli imply that
Figure 4 depicts the effect on the viscoelastic
moduli of Eqs. (35-37) of an increase in dipolar magnetic strength for a fixed
concentration of the ferrofluid. In this case, the theory predictions show the same
trends as our simulation calculations. However, the predicted module provides only a
qualitative agreement. In Figs. 5 and 6 are provided the longtime (
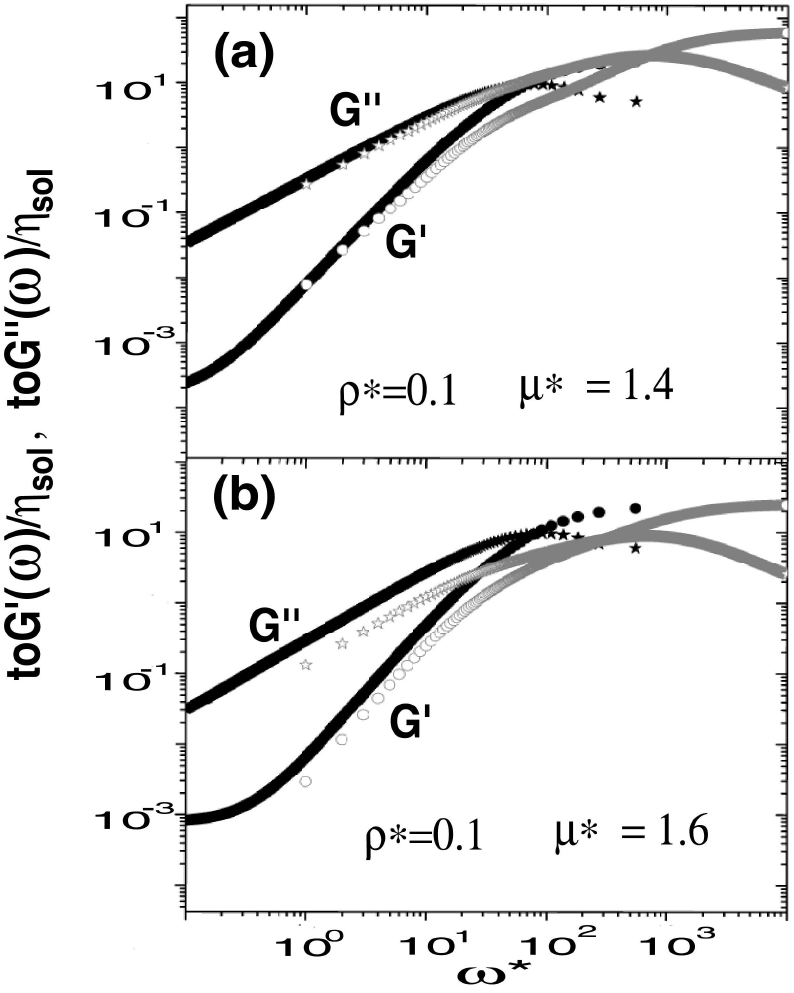
Figure 4. Logarithm of viscoelastic moduli versus frequency and two dipolar
strength and fixed concentration. Theory for G' is
denoted with symbol
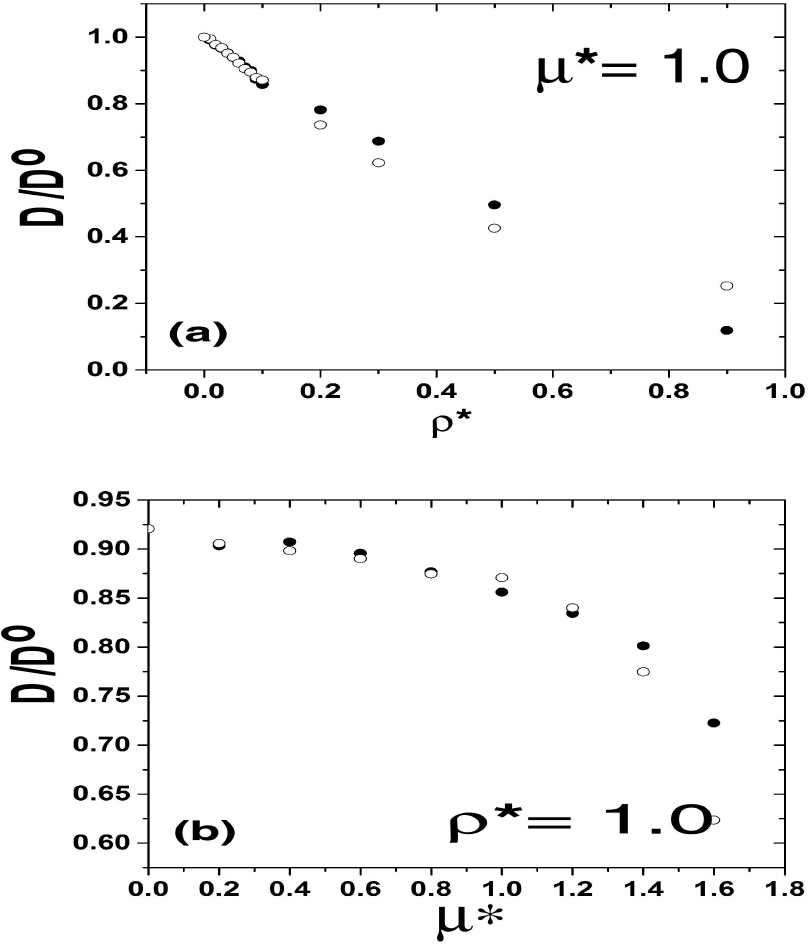
Figure 5. Translational self-diffusion coefficient
D/D0 versus; density
(a) and dipole strength (b). Simulation calculations are depicted with
symbol

Figure 6. Rotational self-diffusion coefficient DR /
Whereas for the rotational diffusion
G'' is given further by Eq. (45) below,
j1(x) is the spherical Bessel
function of order 1 and
In Figs. 5 and 6 simulation values are given by symbol
5. Rotational diffusion microrheology
In this section, we provide the viscoelastic moduli of the ferrofluid when the probe particle performs rotational Brownian motion 7. From the friction function of Eq. (17) for the rotational diffusion of the probe particle we obtained the elastic modulus of the magnetic fluid
And the viscous modulus is
We propose to use our Eqs. (35-37) and (41) for the rheology of ferrofluids in an experimental
study as follows: Ferro-particles need to be made with a fluorescence dye in order
they do not absorb all light in experiments of video microscopy which allows
determining their positions. At low concentration and a proper selection of
wavelength as indicated in Ref. 4
may allow for this case. Since the measurement of each particle orientation would be
difficult, even with the determination of the spatial coordinates, it is feasible to
obtain the radially symmetric component g(r) of the pair correlation function using
Eqs. (38) moreover, (39). Thus, it can be ignored the transversal contributions
mnl = 110, 112. We have observed that for very low or very high
concentrations the dipolar dependent terms are much smaller either in the
viscoelastic moduli of Eqs. (35,37) , Eq. (41), and in the diffusion coefficients,
Eqs. (42-43), then their symmetric parts which depend on
h000. The resulting expressions will still depend
only on the radially symmetric
6. Conclusions
Using a Langevin equation approach we derived analytical expressions for the elastic G' and loss modulus G'' valid in linear viscoelasticity of a ferrofluid and no external magnetic fields. We approximated the collective dynamic of fluctuation in concentration regarding a single relaxation time. Such temporal decay of thermal fluctuations coincides with a Maxwell model of viscoelasticity. These expressions depend on the microstructure of the magnetic fluid through the structure factor determined by direct particle interactions. For model systems at different thermodynamic states of equilibrium, magnetic moment and concentration, the prediction of the viscoelasticity yields the observed trends that result from Langevin dynamic calculations. At low frequencies of thermal fluctuations of polarization, the dissipative mode is dominant. At high frequencies, the ferrofluid behaves as an elastic material. The viscous modulus at long times relates to the self-diffusion coefficient of translational and rotational diffusion of a ferro-particle. We point out that the approach presented in our manuscript allows the determination of three essential dynamical properties of the magnetic suspension: the viscosity, translational and rotational tracer diffusion coefficients. Both diffusion coefficients display the same tendency as the results of simulation calculations. In a forthcoming manuscript, we introduce our extension of the present approach to include time-dependent external magnetic and electric fields acting on ferrofluids in the regime of applied linear stationary shear flows and its comparison with existing experiments.











 nueva página del texto (beta)
nueva página del texto (beta)