nueva página del texto (beta)
Español (pdf)
Artículo en XML
Referencias del artículo
Traducción automática
Enviar artículo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
Con la constante evolución de las plataformas digitales, acompañada del crecimiento en las técnicas de computación y comunicación, se han logrado establecer comunidades que reúnen a agentes provenientes de todo el mundo. Este progreso trajo consigo el auge en el uso de las criptomonedas que tienen la característica de utilizar la criptografía para seguridad de sí mismas (Lojo, 2018) y aunque en la actualidad existe una diversidad de ellas, la primera que se introdujo bajo la tecnología de cadenas de bloques (blockchain) fue el Bitcoin (BTC) en 2008 por medio de un grupo de programadores bajo el seudónimo de Satoshi Nakamoto (Cheah y Fry, citado en Haque, Hassan y Alon, 2019).
Esta criptomoneda opera sin una supervisión que garantice las transacciones financieras, es decir, circula de forma descentralizada, por lo que funciona bajo un consenso entre los usuarios y programadores para que el código no sea alterado (García, 2019). Su valor en el mercado cambia al igual que cualquier otra divisa, hasta septiembre de 2021 tiene una capitalización de mercado de 2.818 billones de dólares (Investing, 2021).
Vale decir que por el hecho de no tener algún activo que respalde su valor, su cotización se vuelve volátil y susceptible a la especulación. De ahí la importancia de que inversores, coberturistas, arbitrajistas y especuladores conozcan la forma en que se relaciona con otras variables económicas y financieras.
Por la sensibilidad del comportamiento del Bitcoin es de interés analizar si tiene un efecto de derrame de volatilidad con otros activos, en otras palabras, si la inestabilidad del precio de la criptomoneda se transmite a otros mercados de interés, tales como el de valores, metales, energético, entre otros. En este sentido, es complicado que los inversores ignoren la relación de dependencia que existe entre los mercados puesto que su prioridad de tener rendimientos en inversiones podría resultar afectado si no gestionan sus portafolios con una adecuada diversificación de riesgos, más aún con la reciente pandemia causada por la enfermedad COVID - 19 que provocó que los mercados bursátiles fluctuaran y provocaran un derrame de riesgos financieros entre distintos mercados (Wang, Wei, Wang y Liu, 2022).
En consecuencia, los commodities han sido utilizados como herramientas de cobertura ante variaciones inesperadas en el mercado, dado que numerosas investigaciones los han descrito como coberturas efectivas contra las variaciones del riesgo (Lahiani, Mefteh-Wali, y Vasbieva, 2021;Mensi, Rehman, Hammoudeh, y Vo, 2021; Majumder, 2022). Por esta razón, es de especial relevancia estudiar la relación en términos del derrame de volatilidad con el mercado de las criptomonedas.
En particular, esta investigación tiene por objetivo analizar la dependencia y el impacto del precio del petróleo, del oro y la volatilidad del mercado de valores sobre el precio del Bitcoin en el periodo de febrero de 2012 a septiembre de 2021 por medio de un modelo GARCH multivariado de tipo diagonal BEKK bajo la hipótesis de la existencia de un efecto de derrame de volatilidad entre las variables.
El aporte de este trabajo se desprende de que con la información generada para los participantes del mercado y autoridades monetarias o regulatorias podrán anticiparse ante las nuevas noticias o comportamientos para diversificar el riesgo y tomar áreas de oportunidad. Además, se contribuye a la literatura empírica con el estudio de los commodities seleccionados y estudiados bajo modelos de la familia GARCH multivariados, en especial de la técnica diagonal BEKK.
Seguido de esta introducción, este estudio se divide en tres secciones. En la primera se revisa la literatura relacionada con la investigación sobre el comportamiento de los precios del Bitcoin, así como las variables con las que se le relaciona y los métodos utilizados. En la segunda parte se presenta la metodología ejecutada este trabajo y luego se presentan los resultados de las estimaciones en la siguiente sección. Por último, se ubican las conclusiones derivadas de esta investigación.
I. Revisión de la literatura
Los estudios sobre el comportamiento de las criptomonedas incrementaron en los últimos años, específicamente, la exploración relacionada con la dinámica de sus precios. De modo que existen investigaciones (Lojo, 2018 y Mayorga, 2019) que relacionan la determinación del precio de las criptomonedas con variables macroeconómicas como el tipo de cambio y la inflación, así como autores (García y Valderrama, 2019; Gómez, 2016; Gracia y Hurtado, 2019) que examinan la relación del precio de las criptomonedas con variables del mercado financiero, en las que, eventos mundiales de incertidumbre, el precio del oro, la especulación y el comportamiento de las economías avanzadas tienen un rol significativo para la determinación de sus precios.
Por su parte, estudios como el de Jalal, Sargiacomo y Sahar (2020) donde asocian a los principales commodities como el oro, la plata, el platino y el petróleo crudo con la volatilidad del precio del Bitcoin a través de modelos GARCH y EGARCH, tienen como resultado la confirmación de un comportamiento volátil de largo plazo de la criptomoneda, en las que únicamente la plata impacta en la volatilidad en comparación con los precios del platino y el petróleo. De ello deriva la sugerencia sobre la posibilidad de utilizar al Bitcoin como diversificador de riesgo.
Además de su relación con los commodities anteriormente mencionados, la investigación de Maghyereh y Abdoh (2020) asocia al Bitcoin con otros activos financieros como tipos de cambio, acciones y el mercado de bonos por medio del enfoque de dependencia espectral cruzada. Sus principales hallazgos muestran evidencia de la dependencia de largo plazo en la cola derecha de la distribución entre los rendimientos del Bitcoin y del índice S&P 500, de forma más débil, una dependencia entre la criptomoneda y el tipo de cambio USD/EUR, así como una relación de corto plazo con los commodities. Igualmente prueban causalidad unidireccional desde los activos financieros hacia el Bitcoin.
Bajo los motivos relacionados al nacimiento del Bitcoin, específicamente sobre el objetivo de ser una moneda descentralizada y con ello solucionar la desconfianza e incertidumbre del sistema financiero, nace la motivación de explorar su correspondencia con índices que representen la incertidumbre de la volatilidad. En este sentido, autores han optado por utilizar al índice de volatilidad de mercado (VIX) del Chicago Board Options Exchange (CBOE) como una variable representativa de la incertidumbre financiera.
Por ejemplo, Al-Yahyaee, Rehman, Mensi, y Al-Jarrah (2019) a través de un enfoque de ondícula bivariada y multivariada analizan el co-movimiento entre el índice VIX y el Bitcoin. Los resultados narran una dependencia entre el BTC - VIX que cambia a través del tiempo con instantes de alta y baja frecuencia, así mismo, el índice VIX se describe como un poderoso predictor sobre el rendimiento del Bitcoin sin importar el nivel de frecuencia.
Por su parte, Soldevilla Estrada (2017), a través de pruebas de causalidad de Granger entre los pares: precio del Bitcoin y el VIX y la volatilidad realizada del Bitcoin y el VIX, consuma la existencia de una relación bidireccional entre las series. De forma contraria, en el estudio realizado por Wang, Xie, Wen, y Zhao (2019), se toma al índice VIX como parte de la representación para medir el riesgo de derrame entre la incertidumbre de la política económica (EPU) y el Bitcoin. Los autores concluyen que el riesgo de efecto de derrame desde EPU a Bitcoin es insignificante en la mayoría de las condiciones.
Respecto al uso de modelos GARCH multivariados para medir la relación entre el Bitcoin, commodities e indicadores de volatilidad, Ghorbel y Jeribi (2021) analizan la relación de la volatilidad entre cinco criptomonedas, índices de las bolsas de valores estadounidenses, el petróleo y el oro mediante un modelo BEKK - GARCH y DCC - GARCH. Los resultados evidencian un alto derrame de volatilidad y de correlación con el Bitcoin. A su vez la correlación tiene un comportamiento dinámico.
Mientras tanto, Hsu, Sheu y Yoon (2021) aplican un modelo diagonal BEKK para investigar el riesgo de derrame de las tres principales criptomonedas a las monedas tradicionales más populares y a los precios spot del oro y los futuros en el periodo de agosto de 2015 a junio del 2020. Los resultados revelan efectos significativos de derrame de volatilidad entre las variables mencionadas, especialmente durante el periodo de incertidumbre generado por la pandemia COVID-19. Igualmente, Fakhfekh, Jeribi, Ghorbel, y Hachicha (2021) con ayuda de modelos DCC, ADCC y GO - GARCH examinan la correlación dinámica entre cinco criptomonedas, el petróleo WTI, el oro, el índice VIX y cuatro bolsas de valores para luego diseñar estrategias de cobertura. Entre los hallazgos se destaca la prueba de que tanto el Bitcoin como el oro tienen elementos de cobertura de materias primas, mientras que el resto demuestran una disposición significativa para actuar como diversificadores. Además, se describe que el VIX es el instrumento más eficaz para cubrir los índices bursátiles de varios reajustes relacionados.
II. Metodología
Modelo diagonal BEKK
El modelo diagonal BEKK propuesto por Engle y Kroner (1995) forma parte de la familia de modelos GARCH multivariados, este modelo es visto como una mejora al modelo VECH y el modelo BEKK tradicional dado que el número de parámetros a estimar se reduce y la matriz de covarianza Ht se mantiene definida positiva (Terrel y Fomby, 2006, tal como se citó en Katsiampa, 2019).
Siguiendo la propuesta original de Engle y Kroner (1995) y la representación generalizada descrita en Reyes (2015:196), el modelo diagonal BEKK se define como
donde C, A y B son matrices de parámetros de tamaño nxn en los cuales los elementos diagonales están restringidos a ser positivos y C tiene la particularidad de ser triangular superior. La diagonal principal de Ht, hii,t representa los términos de la varianza condicional y los elementos fuera de ella son iguales a cero tal como se muestra en la representación matricial de la ecuación 2.
Es necesario destacar que los parámetros estimados del modelo no representan directamente la relación de los términos sobre la matriz de covarianza Ht. De ahí que para lograr una interpretación adecuada es necesario reescribir la ecuación 2 en términos de los efectos ARCH y GARCH tal como sigue.
Las ecuaciones 3, 4 y 5 así como la representación matricial de la ecuación 2 ilustran del caso de un modelo diagonal BEKK bivariado como el que se emplea en este estudio para analizar el derrame de volatilidad entre los tres pares de rendimientos logarítmicos: del Bitcoin (BTC) y el índice de volatilidad de mercado (VIX), del Bitcoin y el precio del petróleo West Texas Intermediate (WTI) y del Bitcoin y precio del oro (XAU).
Finalmente, de acuerdo con Katsiampa (2019:223) la correlación condicional dinámica entre las variables se determina conforme a la ecuación 6
donde h11,t es la varianza condicional del Bitcoin, h22,t es la varianza condicional del índice VIX (o el precio del petróleo o el precio del oro) y h12,t es la varianza condicional.
III. Resultados
Datos
Para representar el petróleo se utiliza como referencia el precio spot del West Texas Intermediate (WTI/USD) puesto que además de ser el commodity más comerciado a nivel internacional, influyó de manera significativa en el precio mundial del petróleo crudo compuesto por el WTI, Brent y el Dubai/Oman (Asianto, 2019). Sobre el precio del oro, se utiliza su precio spot (XAU/USD) al igual que para el Bitcoin (BTC/USD). De estas variables listadas se toman los precios de cierre diarios expresados en dólares estadounidenses.
Finalmente, para la volatilidad de los mercados de valores se emplea el índice de volatilidad del mercado (VIX) del Chicago Board Options Exchange (CBOE), debido a que contiene información sobre la cotización media de las opciones de compra y venta del índice S&P500 y con ello se obtiene una medida de volatilidad esperada a 30 días del mercado de valores de Estados Unidos (Chicago Board Options Exchange, s.f.).
Debido al contraste en la frecuencia de cotización de los activos mencionados1, se realizó una alineación de las series con la finalidad de tener el mismo tamaño de muestra y periodo de tiempo. Hecha esta salvedad, los datos comprenden el intervalo del 02/02/2012 al 03/09/2021 con frecuencia diaria, teniendo un total de 2,414 observaciones para cada variable. Estos se obtuvieron de la página Investing (2021) y Yahoo Finance (2021).
Análisis gráfico
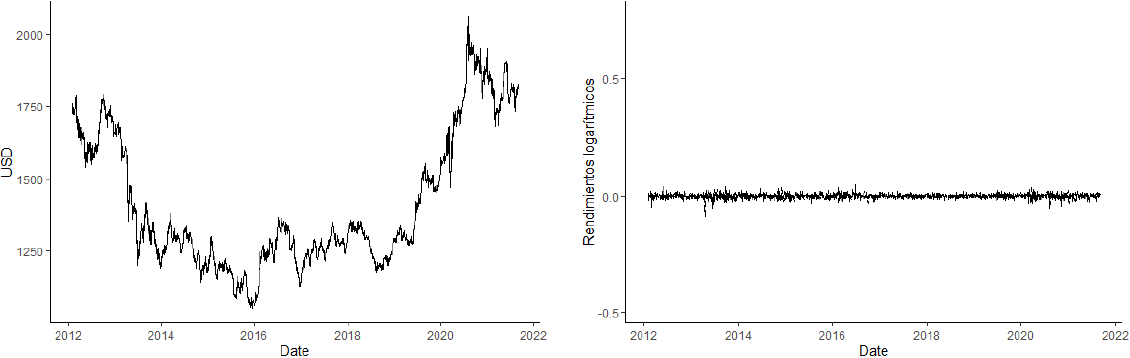
Las tendencias de las variables bajo estudio se observan crecientes con excepción del precio spot del WTI que mantiene una tendencia a la baja. De acuerdo con la Gráfica 1, el comportamiento de los precios del Bitcoin inicia su relevancia en diciembre del 2013 puesto que por primera vez rompió el techo de los 1,000 dólares para caer posteriormente a 500 dólares. Este comportamiento abrupto es perceptible en la Gráfica 1 de línea punteada donde se muestran los rendimientos logarítmicos del precio de cierre.
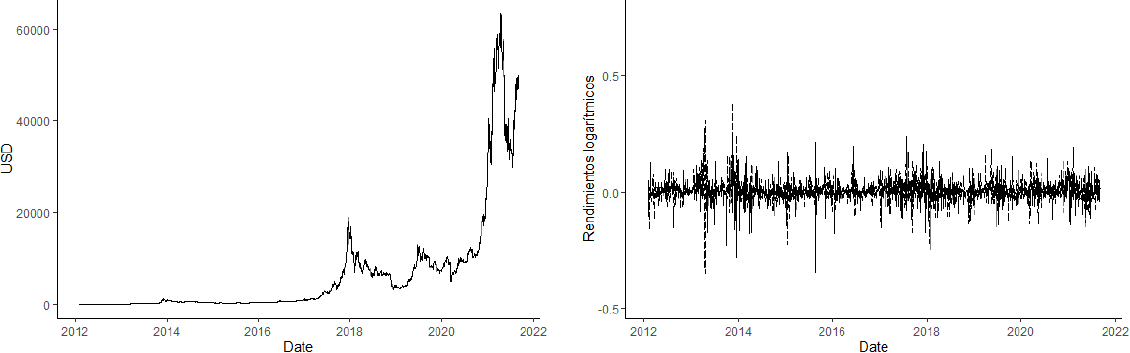
Fuente: elaboración propia con datos de Investing (2021) y Yahoo Finance (2021).
Gráfica 1 Precio de cierre del Bitcoin (BTC) en niveles y rendimientos logarítmicos
Luego de este episodio, la criptomoneda continúa con una cotización moderada creciente entre los 310 y 1,000 dólares hasta principios de 2017. A partir de ello se contempla un crecimiento exponencial en su valor como consecuencia del inicio del Brexit en Europa y el comienzo de la presidencia de Donald Trump en Estados Unidos, estos hechos condujeron a que el Bitcoin consiguiera su segundo precio máximo histórico en diciembre de 2017 con un precio cercano a los 19,000 dólares. De forma paralela a esta etapa de crecimiento, también se observa un periodo cambiante en los retornos logarítmicos de los precios diarios.
Finalmente, inicia la nueva etapa alcista en 2020 y hasta el primer trimestre del 2021 luego de la pronunciada caída que llevó el valor de la criptomoneda a los 5,400 dólares por el gran confinamiento a causa de la pandemia por el coronavirus. Esta situación afectó de forma significativa a los rendimientos del Bitcoin puesto que es el cambio más bajo de su valor histórico.
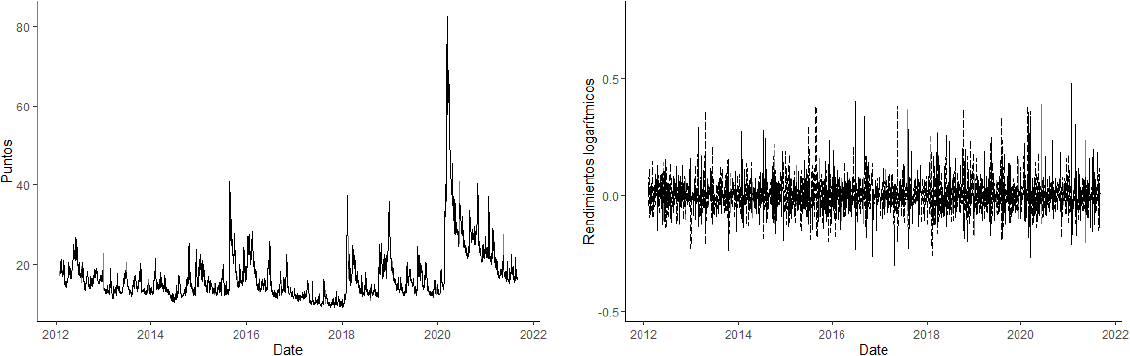
Por otra parte, el índice de volatilidad de mercado (VIX) presenta un periodo de inestabilidad como se muestra en la Gráfica 2 luego de su comportamiento habitual hasta mediados de 2015, debido a una tendencia bajista en el precio de los principales commodities como el petróleo crudo y el oro tal como se observa en las Gráficas 3 y 4. Aunado a ello existió la incertidumbre respecto a la recuperación económica de la zona euro y Japón, así como la desaceleración económica en Estados Unidos.
Fuente: elaboración propia con datos de Investing (2021) y Yahoo Finance (2021).
Gráfica 2 Índice de volatilidad de mercado (VIX) en niveles y rendimientos logarítmicos
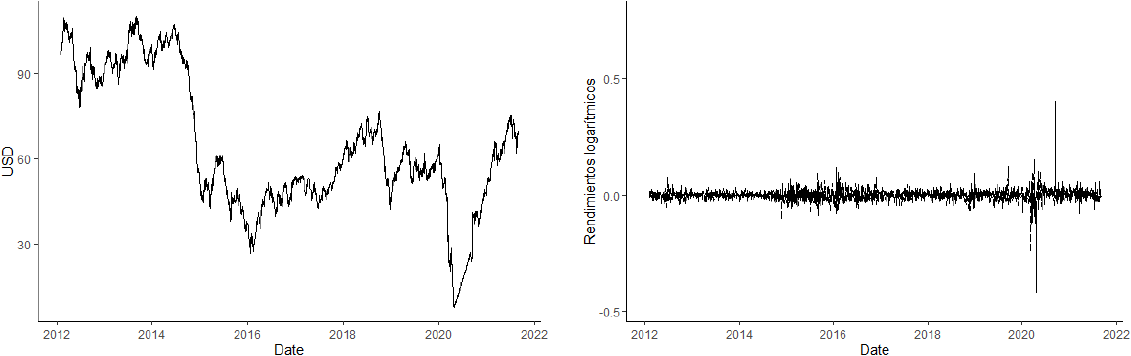
Fuente: elaboración propia con datos de Investing (2021) y Yahoo Finance (2021).
Gráfica 3 Precio spot del petróleo crudo (WTI) en niveles y rendimientos logarítmicos
Fuente: elaboración propia con datos de Investing (2021) y Yahoo Finance (2021).
Gráfica 4 Precio de cierre del oro (XAU) en niveles y rendimientos logarítmicos
Posteriormente, en 2018 se observa un cambio radical en los rendimientos logarítmicos del VIX que coincide con el incremento en la volatilidad causado por el conflicto comercial entre Estados Unidos y China al igual que las tensiones diplomáticas entre Estados Unidos y Corea del Norte. Por último, la reacción de los mercados en marzo 2020 provocó el mayor episodio de volatilidad registrado en el periodo como consecuencia del anuncio de la Organización Mundial de la Salud (OMS) en la que oficialmente se declaraba el brote de coronavirus como pandemia. De manera reciente, se observa un comportamiento a la baja muy cercano a los niveles históricos habituales.
Respecto al precio del oro, su rendimiento logarítmico se vio afectado de manera importante desde octubre del 2012 hasta inicios de 2016 con un cambio característico en junio de 2013 como resultado del abandono progresivo por parte de los inversores y la sustitución de este por otros activos financieros luego de que cubrieron su riesgo en la crisis financiera de 2008. Posterior a un periodo de estabilidad, en la mitad del 2018 inicia un periodo de cotización alcista que se interrumpe a finales del 2020 para continuar con un comportamiento volátil por el efecto de la pandemia del coronavirus en los mercados internacionales.
Estadísticos descriptivos
De acuerdo con lo expuesto en el Cuadro 1, el Bitcoin (BTC/USD) se observa como el activo más cotizado puesto que su precio promedio en dólares se ubica por encima del resto de las variables y tiene los mínimos y máximos niveles de apreciación. En cambio, también es la más volátil puesto que tiene la mayor desviación estándar al igual que los rendimientos logarítmicos del índice de volatilidad de mercado (VIX), puesto que por su naturaleza permite capturar los movimientos inestables del mercado.
Cuadro 1 Estadísticos descriptivos de las variables en niveles y primeras diferencias del logaritmo natural
| Media | 6443.93 | 64.32 | 1410.17 | 16.97 | 0.00 | 0.00 | 0.00 | 0.00 |
|
Desviación estándar |
11665.2 5 |
23.72 | 232.94 | 6.9 | 0.05 | 0.03 | 0.01 | 0.08 |
| Sesgo | 2.88 | 0.21 | 0.78 | 3.44 | -0.55 | -1.77 | -0.68 | 1.2 |
| Curtosis | 8.2 | -0.73 | -0.64 | 19.47 | 9.99 | 66.02 | 6.52 | 6.94 |
| Jarque-Bera1/ | 10115 (0.000)* |
70.423 (0.000)* |
288.1 (0.000)* |
42949 (0.000)* |
10185 (0.000)* |
440291 (0.000)* |
4475.2 (0.000)* |
5435.7 (0.000)* |
| Mínimo | 4.3 | 7.79 | 1051.74 | 9.14 | -0.48 | -0.42 | -0.09 | -0.3 |
| Máximo | 63518 | 110.3 | 2063.19 | 82.69 | 0.38 | 0.4 | 0.05 | 0.77 |
| ADF 2/ | -0.54798 (0.9796) |
-1.6459 (0.7282) |
-2.0158 (0.5717) |
-5.528 (0.01)** |
-11.083 (0.01)** |
-12.843 (0.01)** |
-13.309 (0.01)** |
-15.518 (0.01)** |
| KPSS 3/ | 12.557 (0.01)** |
13.206 (0.01)** |
7.4103 (0.01)** |
3.96 (0.01)** |
0.1586 (0.1) |
0.0972 (0.1) |
0.4183 (0.06923) |
0.0102 (0.1) |
Fuente: elaboración propia
Δ=operador de primera diferencia
1/Hipótesis nula: normalmente distribuidos
2/Hipótesis nula: no estacionario
3/Hipótesis nula: estacionariedad
***significativo al 5%
Otro rasgo de los estadísticos descriptivos es que la mayoría de las variables en niveles se comportan con una curtosis y sesgo positivos. De forma contraria, para el petróleo West Texas Intermediate (WTI/USD) y el precio en dólares del oro (XAU/USD), la curtosis es negativa. Esto significa que las variables tanto en niveles como transformadas presentan valores atípicos y una forma no simétrica del sesgo en comparación con una distribución normal. En este sentido, con ayuda del estadístico de Jarque - Bera es posible determinar bajo una prueba de hipótesis la distribución normal (o no) de los datos. Según los resultados de esta prueba en el Cuadro 1, se infiere que las variables en cuestión no tienen una distribución normal y de ahí que este estudio emplea una distribución t - student en la distribución empírica de los datos para capturar el efecto de exceso de curtosis y de colas largas y pesadas (no normalidad). Por último, en las pruebas, Aumentada de Dickey - Fuller (ADF) y Kwiatkowski-Phillips-Schmidt-Shin (KPSS), se contempla la estacionariedad de las series en las primeras diferencias de los rendimientos logarítmicos y con ello se garantiza su comportamiento estable a lo largo del tiempo.
Prueba ARCH-LM
Considerando que el comportamiento de los activos tiene una varianza condicional variable en el tiempo, es necesario determinar si las mismas evolucionan con una varianza constante, es decir, si presentan efecto ARCH. Para evaluar la significancia de este efecto, se utiliza la prueba ARCH - LM introducida por Engle (1982) ya que considera que las variables de naturaleza financiera no tienen una varianza constante en la muestra y se verifica a través de la hipótesis nula de no heteroscedasticidad.
Con los resultados expuestos en el Cuadro 2 se infiere que los rendimientos logarítmicos del precio del Bitcoin, del petróleo WTI, del oro y el índice VIX tienen efecto ARCH. Con ello se justifica y da soporte al uso de metodologías de modelos multivariados GARCH como el que se propone en este estudio para modelar las varianzas condicionales y estudiar los efectos de transmisión de la volatilidad entre ellos (Katsiampa, 2019). Además, estos modelos no asumen una varianza condicional constante de los datos como los modelos econométricos tradicionales.
Cuadro 2 Detección de efecto ARCH
| Variable | Prueba ARCH-LM1/ |
|---|---|
| ΔlnBTC | 288.61 (0.000)*** |
| ΔlnVIX | 103.11 (0.000)*** |
| ΔlnWTI | 358.83 (0.000)*** |
| ΔlnXAU | 98.812 (0.000)*** |
Fuente: elaboración propia
1/ La prueba estadística ARCH-LM es el multiplicador de Lagrange usado para la detección del efecto ARCH. Bajo la hipótesis nula de no heteroscedasticidad, dicho término se distribuye como λ 2(k).
***significativo al 5%
Elección del modelo
Para elegir el modelo óptimo que describa en mayor proporción el comportamiento de las series asumiendo una distribución t-student, se utiliza el criterio de información de Akaike (AIC), Schwarz (SIC) y de Hannan - Quinn (H - Q) tal como se muestra en el Cuadro 3. Conforme a los resultados y los criterios de información, se señala que el mejor modelo es la especificación BEKK (1,2) para la relación entre el Bitcoin y el índice de volatilidad del mercado (VIX), el precio del petróleo (WTI) y el del oro (XAU).
Cuadro 3 Elección del modelo diagonal BEKK (p,q)
| GARCH (p) ARCH (q) |
Criterio de información1/ |
ΔlnBTC- ΔlnVIX |
ΔlnBTC- ΔlnWTI |
ΔlnBTC - ΔlnXAU |
|---|---|---|---|---|
| BEKK (1,1) | AIC | -6.00259 | -8.56509 | -10.23203 |
| SIC | -5.97860 | -8.54110 | -10.20804 | |
| H - Q | -5.99387 | -8.55636 | -10.22330 | |
| BEKK (1,2) | AIC | -6.02217* | -8.57876* | -10.23722* |
| SIC | -5.99338* | -8.54997* | -10.20844* | |
| H - Q | -6.01170* | -8.56829* | -10.22675* | |
| BEKK (2,1) | AIC | -6.00973 | -8.57824 | -10.23150 |
| SIC | -5.98095 | -8.54946 | -10.20271 | |
| H - Q | -5.99927 | -8.56777 | -10.22103 | |
| BEKK (2,2) | AIC | -6.02056 | -8.41906 | -10.23579 |
| SIC | -5.98698 | -8.38547 | -10.20221 | |
| H - Q | -6.00835 | -8.40685 | -10.22358 |
Fuente: elaboración propia
1/ AIC = Criterio de Información de Akaike
SIC = Criterio de Información de Schwarz
H - Q = Criterio de información de Hannan-Quinn
Valor mínimo del criterio de información marcado por (*)
Modelo diagonal BEKK
Los resultados de la estimación del modelo diagonal BEKK (1,2) se presenta en el Cuadro 4. De ello se observa que el parámetro a11 es estadísticamente significativo en todos los pares de variables y el valor correspondiente a a22 únicamente en la relación ΔlnBTC -ΔlnVIX y ΔlnBTC - ΔlnWTI. Su importancia de identificación radica en que según lo descrito en la ecuación 4 es posible interpretar que, en las relaciones antes mencionadas, los choques rezagados en un periodo en el Bitcoin (VIX) tienen una influencia de 0.13417 para la volatilidad actual del VIX (Bitcoin) y de 0.04316 los choques rezagados en un periodo del Bitcoin (WTI) en la volatilidad actual del WTI (Bitcoin). De igual modo ocurre con estos parámetros para el segundo rezago, sin embargo, la asociada al Bitcoin no refleja ser significativa para la relación ΔlnBTC - ΔlnWTI y ΔlnBTC - ΔlnXAU. Para el caso de ΔlnBTC -ΔlnVIX resulta ser de menor importancia puesto que apenas logra ser de 0.08466.
Cuadro 4 Resultados de la estimación diagonal BEKK (1,2)
| Parámetro |
ΔlnBTC - ΔlnVIX |
ΔlnBTC- ΔlnWTI |
ΔlnBTC- ΔlnXAU |
|---|---|---|---|
| c11 | 0.008209 (0.0000)*** |
0.007676 (0.0000)*** |
0.008007 (0.0000)*** |
| c12 | -0.008563 (0.4357) |
0.000195 (0.4385) |
0.000152 (0.1240) |
| c22 | 0.042412 (0.0000)*** |
0.003175 (0.0000)*** |
0.001011 (0.0000)*** |
| a11,1 | 0.371965 (0.0000)*** |
0.410241 (0.0000)*** |
0.414146 (0.0000)*** |
| a22,1 | 0.360706 (0.0000)*** |
0.105208 (0.0196)*** |
0.024987 (0.8215) |
| a11,2 | 0.222633 (0.0548)** |
0.000000 (1.0000) |
0.105814 (0.5630) |
| a22,2 | 0.380280 (0.0001)*** |
0.319870 (0.0000)*** |
0.199171 (0.0000)*** |
| b11,1 | 0.901147 (0.0000)*** |
0.906144 (0.0000)*** |
0.904033 (0.0000)*** |
| b22,1 | -0.718277 (0.0000)*** |
0.941597 (0.0000)*** |
0.977807 (0.0000)*** |
| df | 3.765714 (0.0000)*** |
4.346388 (0.0000)*** |
3.816055 (0.0000)*** |
Fuente: elaboración propia
***significativo al 5%, **significativo al 10%
Consideremos ahora a los términos b11 y b22, los cuales son significativos para todas las especificaciones, estas se traducen en el efecto GARCH de los modelos, es decir, la persistencia de la volatilidad rezagada en un periodo. En particular, la persistencia es negativa para la relación ΔlnBTC - ΔlnVIX de magnitud -0.64727 y positiva para ΔlnBTC - ΔlnWTI y ΔlnBTC - ΔlnXAU en la cual esta última presenta el mayor grado con valores de 0.85322 y 0.88397, respectivamente.
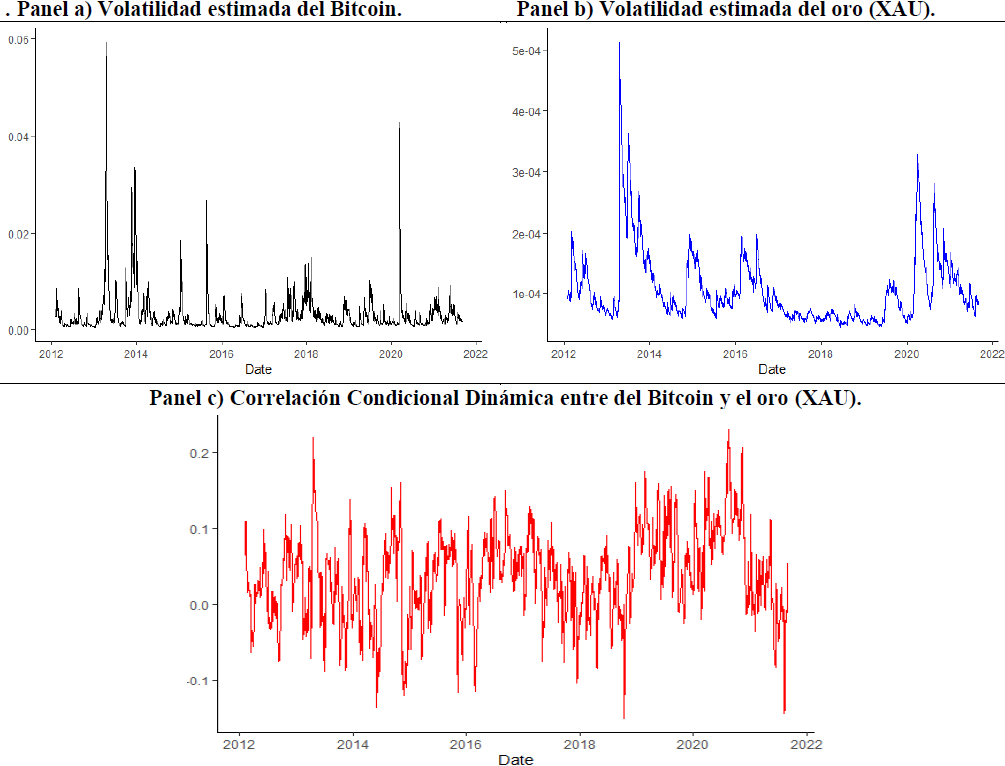
Acerca de la correlación condicional dinámica, el panel c) de las Gráficas 5, 6 y 7 muestra que en promedio existe una dependencia negativa (-0.016322) entre el Bitcoin y el índice VIX, lo cual podría deberse a que, ante la incertidumbre en el mercado de valores (del Bitcoin), los inversionistas buscan cubrirse del riesgo a través de la compra de bitcoin (de activos en el mercado de valores). Para el caso del oro (XAU) la correlación promedio es mayor (0.037194) en comparación con el petróleo (WTI) (0.013503), esto implica un derrame de volatilidad más fuerte en los mercados BTC - XAU.
Vale decir que el comportamiento de la correlación entre el oro y el petróleo es distinto en vista de que con este último existe una dinámica más estable mientras que con el oro, los rangos de movimiento en este parámetro son más dispersos. Además, puede observarse de forma reciente que con la crisis causada por la enfermedad COVID-19, el comportamiento en la dependencia de los valores fue mayormente negativa en el oro por su caída repentina en la volatilidad.
Estos resultados son congruentes a investigaciones similares como las de Mensi, Sensoy, Aslan, y Kang, (2019); Okorie y Lin (2020); Hsu, Sheu y Yoon (2021); Ghorbel y Jeribi (2021) y Fakhfekh, Jeribi, Ghorbel, y Hachicha (2021), donde se ha evidenciado el efecto de derrame de volatilidad y la cuantificación de la correlación entre el Bitcoin, el petróleo WTI, el índice de volatilidad VIX y el precio del oro.
Validación del modelo
Para asegurar la validez estadística del modelo diagonal BEKK y la correcta interpretación de los resultados, se elaboran las pruebas de Hosking (1980) y McLeod - Li (1983) con la finalidad de evaluar la significancia de la correlación serial y la heteroscedasticidad condicional autorregresiva en los cuadrados de los residuos estandarizados del modelo. Estas pruebas se han utilizado en varios estudios con distintos tipos de modelos GARCH multivariados (Akhtaruzzaman, Sensoy y Corbet, 2020; López y Sosa, 2021; Alkathery y Chaudhuri, 2021; Diaz, 2021) para confirmar que después de la modelación, los residuos están libres de correlación serial y efecto ARCH y, por tanto, otorgar robustez al modelo.
Los resultados de las pruebas reportados en el Cuadro 5 muestran a los residuos estandarizados de los pares ΔlnBTC -ΔlnVIX y ΔlnBTC - ΔlnWTI sin correlación serial y sin heteroscedasticidad condicional autorregresiva en todos los rezagos y en el rezago 50 para el par ΔlnBTC - ΔlnXAU. Otorgando así robustez estadística al modelo diagonal BEKK y validez a la interpretación de los resultados.
Cuadro 5 Prueba de Hosking (1980)1/ y Mcleod - Li (1983)2/ sobre el cuadrado de los residuos estandarizados hasta el rezago k.
| Prueba | Rezago |
ΔlnBTC- ΔlnVIX |
ΔlnBTC- ΔlnWTI |
ΔlnBTC- ΔlnXAU |
|---|---|---|---|---|
| Hosking | 5 | 24.7755 (0.09984) |
15.9228 (0.52931) |
78.8032 (0.00000)*** |
| 10 | 35.1313 (0.55688) |
25.9842 (0.91244) |
87.6317 (0.00000)*** |
|
| 20 | 62.2578 (0.88855) |
31.4183 (0.99999) |
105.574 (0.01703)*** |
|
| 50 | 136.044 (0.99969) |
130.098 (0.99993) |
175.717 (0.85982) |
|
| McLeod - Li | 5 | 24.7698 (0.09998) |
15.9287 (0.52889) |
78.7874 (0.00000)*** |
| 10 | 35.1548 (0.55577) |
26.0204 (0.91158) |
87.6530 (0.00000)*** |
|
| 20 | 62.3531 (0.88687) |
31.6753 (0.99999) |
105.747 (0.01656)*** |
|
| 50 | 136.854 (0.99962) |
130.649 (0.99992) |
176.640 (0.84836) |
Fuente: elaboración propia
1/ Hipótesis nula: Los residuos no presentan correlación serial
2/ Hipótesis nula: No hay heteroscedasticidad condicional autorregresiva
***significativo al 5%
Conclusiones
Esta investigación analiza la dependencia y el impacto del precio del petróleo, del oro y la volatilidad del mercado de valores sobre el precio del Bitcoin a través de un modelo GARCH multivariado de tipo diagonal BEKK dentro del periodo de febrero de 2012 a septiembre de 2021 con el objetivo de probar que existe un efecto de derrame de volatilidad entre las variables. Los resultados señalan que se cumplió la hipótesis sobre la presencia de este efecto para todos los pares de variables en términos de sus rendimientos logarítmicos, esto es, entre el Bitcoin (BTC) y petróleo West Texas Intermediate (WTI), el Bitcoin y el índice de volatilidad de mercado (VIX) y el Bitcoin y el oro (XAU).
Por una parte, los choques rezagados en el periodo anterior dentro de la relación BTC - VIX resultan tener la influencia más representativa en comparación con el resto de las variables, mientras que cuando se consideran dos periodos anteriores, los choques en el BTC mostraron no tener importancia para determinar la magnitud del derrame de volatilidad actual cuando se asocia con el WTI y el oro. Cuando este mismo se relaciona con el índice VIX, es mínimo. En este sentido, la influencia de la volatilidad anterior mostró tener mayor relevancia en la dependencia entre el BTC y el oro, al mismo tiempo que fue negativa dentro del par BTC - VIX.
La correlación condicional dinámica describe ser negativa en la relación BTC - VIX debido a que los inversionistas buscan cubrirse del riesgo a través de la compra de otros activos cuando existe incertidumbre en el mercado de valores o de criptomonedas. A su vez, la correlación promedio del Bitcoin fue mayor con el oro en comparación con el petróleo, sin embargo, el comportamiento a través del tiempo analizado es más estable con el petróleo. Estos hallazgos son consistentes con otras investigaciones dedicadas a analizar la dependencia de volatilidad y la correlación de las variables anteriormente descritas (Mensi, Sensoy, Aslan, y Kang, (2019); Okorie y Lin (2020); Hsu, Sheu y Yoon (2021); Ghorbel y Jeribi (2021) y Fakhfekh, Jeribi, Ghorbel, y Hachicha (2021).
Esta información sirve a distintos participantes del mercado inversión, diversificación y cobertura de activos financieros puesto que la información es útil para diseñar estrategias enfocadas en análisis de decisiones y aprovechar el comportamiento de las variables estudiadas una vez se conoce la correlación dinámica asociada y la dependencia de sus volatilidades. Igualmente, es útil para las autoridades monetarias y regulatorias preocupadas por la evolución del Bitcoin y su relación con variables representativas de los mercados puesto que su comportamiento podría ser importante en el momento de dictar políticas.
Dentro de las futuras líneas de investigación podría ampliarse la muestra de criptomonedas con el fin de comparar la magnitud del efecto sobre otras variables, también en investigaciones complementarías, agregar herramientas para conocer desde otra perspectiva la causalidad entre las series con el objetivo de realizar inferencia en términos de derrames de volatilidad cruzada o propia. Finalmente, las estimaciones de las varianzas condicionales y las correlaciones dinámicas obtenidas en este estudio proporcionan elementos para considerar la elaboración de portafolios dinámicos en trabajos futuros.
