1. Introduction
The confirmed (g-2)μ anomaly by the Fermilab [1] and the W boson mass new measurement [2], which are not consistent with the theoretical prediction, have shown again that the Standard Model (SM) is incomplete. Along with this, the flavor puzzle remains to be solved so that there is a need to enlarge the SM.
The neutrino oscillation opened the window to search physics beyond the SM, as it is well known, these established that neutrinos have mass so they mix. Although there are many mechanism [3] to get tiny neutrino masses, so far there is no a convincing theory that explains the origin of such mass and the peculiar pattern which is completely different from the quark sector. In the last years, several experiments have measured the neutrino mixing angles with great accuracy, also the masses seem to obey two orderings (normal and inverted hierarchy) due to the lacking of information on the absolute neutrino mass. Certainly, the normal ordering is preferred by the available data [4, 5] but the inverted hierarchy is not completely discarded [6]. Another important point is that, conforming to the experimental data, the PMNS mixing matrix exhibits large values in its entries, in addition, the second and third rows satisfy the relation |Uμi|=|Uτi| (i = 1,2,3) in good approximation for the normal and inverted hierarchy. The aforementioned facts might be understood by means of a symmetry in the effective neutrino mass matrix, then the concept of flavor symmetry turn out being crucial to explain the mixings, and a variety of discrete symmetries [7, 8, 8-14] have been applied to the lepton sector. In particular, the neutrino data seem to obey an approximated μ ↔ τ symmetry (for a complete review see [15]), that consists in the exchange label μ ↔ τ in the effective neutrino mass matrix when the charged lepton mass one is diagonal. Speaking of exact μ ↔ τ symmetry, which is is outdated currently due to its predictions, would imply to obtain 0∘ and 45∘ for the reactor and atmospheric angles, respectively. Besides that, the solar angle and the Dirac CP-violating phase keep as a free and unknown parameters. Despite this, from the model building point of view, the well studied μ ↔ τ symmetry has been a guide to construct lepton models [16-24] and there is a possibility that a soft breaking [21-23, 25-29] of this symmetry can accommodate the experimental results so that there is still strong motivation to study on the μ ↔ τ symmetry. Apart from this, elaborated flavored models have been proposed to face the lepton mixings and related issues as leptogenesis, dark matter, and so forth [14, 30, 31].
On the other hand, in the quark sector, according to the available data [32] the CKM matrix is close to the identity one, this pattern might be explained by the notable hierarchy among the quark masses. In addition, this feature is exhibited by some matrices like the nearest neighbor interactions (NNI) [33-36] and the generalized Fritzsch [37-39] mass textures which can be obtained by means the flavor symmetries [7-10]. The contrasting behavior between the PMNS and CKM mixing matrices is undoubtedly a puzzling problem, so far one of the main task for model builders is to match simultaneously the fermion mixings by the same flavor symmetry in the suitable framework.
In order to address the masses and mixing problem, a phenomenological scalar extension of the SM is realized where the type II see-saw mechanism is responsible to obtain small neutrino masses and special emphasis is put on the lepton sector under a soft breaking of the μ ↔ τ symmetry scheme. To do so, we use the 𝐒4 [40-44, 46-48] non-abelian discrete group to handle the Yukawa couplings, at the same time, this symmetry allows to treat the quark, lepton and scalar sector in different manner. Additionally, we include a 𝐙2 symmetry, to have a non-renormalizable Yukawa mass term for neutrinos. On the other hand, the inclusion of three Higgs doublets are required to obtain the quark and charged lepton masses and mixings, this latter comes out being diagonal as result of the matter assignation under the flavor symmetry. Then, an enriched scalar (flavons) sector is included to provide desirable mass textures. In consequence, the mixings arises from the spontaneous breaking of the S4⊗Z2 discrete group and the μ ↔ τ symmetry is broken in the effective neutrino mass matrix. Eventually, the reactor and atmospheric angles come out being different of 0° and 45° respectively. CP parities phases in the neutrino masses play an important role to get sizable values for θ 13 and the deviation of θ 23 from maximality which turn out being consistent with neutrino data for the inverted hierarchy. In the quark sector, under certain assumptions, the generalized Fritzsch textures shape to the quark mass matrices so that the CKM matrix values are guaranteed.
It is worthy mentioned that a similar study was carried out [24], nonetheless there are clear differences namely. The first one is scalar matter and the flavor symmetry, the second one is related with the mechanism to generate small neutrino masses and the corresponding predictions: in the aforemen- tioned paper, they got exact μ ↔ τ symmetry. Lastly, the NNI textures, in the quark mass matrices, appeared in a natural way so that they obtained correct values for the mixings. Although our model has some limitations like the flavon alignments and one benchmark (in the quark sector), the main purpose of this work was to show that a simple soft breaking of the μ ↔ τ symmetry is enough to correct the lepton mixing angles.
The layout of the paper is as follows. In Sec. 2, we describe the general framework to explore the 𝐒4 discrete symmetry, the full assignation for the matter content is shown and the mass matrices and the corresponding mixing matrix are obtained. In addition, a brief analytical study is carried out to fix some free parameters in the model. Main results are presented in scattered plots where the set of free parameters values, that fit the mixing angles, are shown. All of this is included in Sec. 3. We give some conclusions in Sec. 4.
2. Flavored model
2.1. General framework
Although, there are fascinating theoretical frameworks that can be good candidates to replace the SM, conforming to our interest, a scalar extension of the SM will be considered. Thus, apart from the SM matter content a Higgs triplet (Δ) is required to generate tiny neutrino masses by means the type II see-saw mechanism. Furthermore, extra Higgs doublets and flavon gauge singlets (ϕ, φ and ξ) will be added to provide the CKM and PMNS matrices, respectively. In Table I, we can see the rest of the matter fields.
Table I Matter content.
| Matter | QL=(ud)L | d R | u R | L=(vl) | e R | H=(H+H0) | ΔL=(δ+2δ++δ0-δ+2) |
|---|---|---|---|---|---|---|---|
| SU(3) c | 3 | 3 | 3 | 1 | 1 | 1 | 1 |
| SU(2) L | 2 | 1 | 1 | 2 | 1 | 2 | 3 |
| U(1)Υ | 1/3 | -2/3 | 4/3 | -1 | -2 | 1 | 2 |
The relevant gauge invariant Lagrangian is given by
with ˜H=iσ2H* and the scalar potential
In flavored models, the scalar potential turns out being important to get a viable model, in here, a detailed study on the scalar potential is not the purpose of this paper however we add a comment about it. The 𝐒4 discrete symmetry [7-10] was selected to control the flavor mixings since it has singlet, doublet and triplet irreducible representations (see the Appendix A for more details), this feature represents an advantage for us because the quark and Higgs sector will be assigned in doublets and singlets whereas the lepton sector in triplets. The main achievement to do that is to get desirable mass textures in both sectors.
Along with this, we wish to highlight the scalar potential, where the three Higgs doublets are only involved, has been study exhaustively [49-51]. In the aforementioned paper, three Higgs doublets were assigned under the 𝐒3 group as follows: the first and second family were put in a 𝟐 whereas the third one in 𝟏1. In these circumstances the scalar potential was minimized and the 〈H2〉=〈H1〉 alignment is allowed by the flavor symmetry. Having commented that, we go back to our work where the 𝐒4 flavor symmetry drives the Yukawa couplings as well as the scalar potential. It is worthy mentioned that the non-abelian groups 𝐒4 and 𝐒3 are completely different from each other (𝐒3 is a subgroup of the 𝐒4), however, the 𝐒4 scalar potential with three Higgs doublets can be mimicked from the previous study [49-51]. This asseveration is supported due to the 𝐒4 representation can be decomposed in the 𝐒3 ones [7]. To be more explicit, as we can see in the Appendix B, the irreducible representations 𝟏𝟏, 𝟏𝟐 and 𝟐 of both groups coincide so that the tensor product respects the same rules among them as can be verified. Then, in this sense, similar results are expected for the Higgs alignments because we are using the same assignation for the three Higgs families under the 𝐒4, as one can see in Table II. On the other hand, a complete analysis of the scalar potential is beyond the scope of this work so that the flavor alignments will be considered as a matter of fact.
Table II Assignment under 𝐒4 flavor group. Here, I = 1, 2 and i = 1, 2, 3.
| Matter | Q IL | Q 3L | d IR | d 3R | u IR | u 3R | L i | e iR | H I | H 3 | 𝚫 | 𝛟 | 𝛗 I | 𝛏 i |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 𝐒4 | 2 | 11 | 2 | 11 | 2 | 11 | 31 | 31 | 2 | 11 | 11 | 11 | 2 | 31 |
| 𝐙2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 |
Further to our previous comments, the full symmetry breaks down as follows: SU(3)C⊗SU(2)L⊗U(1)Y⊗S4⊗Z2→SU(3)C⊗SU(2)L⊗U(1)Y→SU(3)C⊗U(1)Q, where the Λ scale of the spontaneous breaking of the S4⊗Z2 group is larger than the 𝑣 = 246 GeV electroweak one.
2.2. The model
Having commented briefly the theoretical framework, we put now attention to the matter field assignation under the 𝐒4 flavor symmetry. Hence, those are assigned as follows: the first and second family of quark and Higgs are put in 𝟐 doublet; the third family is assigned to the 𝟏1 singlet. This choice has been exploited in many 𝐒3 models with three Higgs doublets (see for instance [52]) and interesting mass textures can be obtained, for this reason, the same assignation is used in our work. On the other hand, the lepton sector is treated in different way since the three families of L(e R)left-handed (right-handed) doublets (singlets) are put in the 𝟑1 triplet irreducible representations. This allows to obtain a diagonal charged lepton mass matrix so that the mixings will arise from the neutrino sector where an enriched scalar one is needed as can be seen in Table II. Let us add a comment on the role 𝐙2 symmetry, the main purpose is to prohibit the renormalizable neutrino mass term, ˉL(iσ2)ΔLC.
Consequently, the most relevant terms which are flavor and gauge invariant are written asi
Once the scalar fields get their vev’s, the fermion masses are written as
Evidently, there are too many free parameters in the fermion mass matrices however some ones can be reduce notably by making an alignment in the vev’s of the scalar fields. In particular, 〈H1〉=〈H2〉 will be assumed in the Higgs sector as we already commented. Also, Higgs vev’s have to satisfy the relation √〈H1〉2+〈H2〉2+〈H3〉2=v=246 GeV. For the flavon sector, the alignment that provides a good phenomenology in the neutrino mass matrix is given by
As it is usual, each vev’s of the flavons are set to be proportional to λΛ where λ (0.225) is the Wolfenstein parameter and the cutoff scale of the model.
2.3. Fermion masses and mixings
2.3.1. Lepton sector
As was already commented, we put special emphasis on the lepton sector. To start with, let us focus in the charged lepton sector which is diagonal and the physical masses can be obtained straightforwardly. Nonetheless, a particular alignment was assumed, this is, 〈H1〉=〈H2〉 [49-51] and the principal motivation has to do with the quark sector where outstanding mass textures appear.
As consequence of the mentioned choice in the Higgs sector, the ye2 Yukawa coupling has to be negative and an extra rotations in the fields are necessary to obtain ˆMe=Diag.(me,mμ,mτ)=U†eLMeUeR with Ue(L,R)=S23ue(L,R), therefore ˆMe=u†eLmeueR with
From Eq. (6), one can identify the charged lepton masses
We stress that there are few parameters to adjust the three charged lepton masses and this can be a weak point. This can be solved by including extra flavons however we want to keep the model simple so that this will not be carried out.
In the neutrino sector, on the other hand, due to phenomenological implications in the mass matrix we assume the alignments given in Eq. (5). Along with this, in the standard basis, ℳ v is diagonalized by the 𝐔 v matrix such that ˆMν=Diag.(m1,m2,m3)=U†νMνU*ν with Uν=S23uν, then ˆMν=u†νmνu*ν where 𝐒23 has been shown before and 𝐦 v is given by
Due to the charged lepton mass matrix is diagonal, one can identify clearly the physical masses, see Eq. (7). Therefore, in the effective mass matrix, 𝐦 v , the μ↔τ symmetry is broken because of the difference mμμ≠mττ as one can notice. As result of this, the reactor and atmospheric angles will be deviated from 0° and 45°, respectively. As it is usual, in the context of μ↔τ, the solar angle is a free parameter which can be fixed to the current experimental values but this will get correction since that mμμ≠mττ.
In order to diagonalize the neutrino mass matrix, a perturbative analysis will be done in such a way that the matrix can be written as
where the former matrix possesses exact μ↔τ symmetry and it is broken in the latter one where the dimensionless parameter ϵ≡(mττ-mμμ)/mμμ has been defined and this quantify the breaking. As we observe, this can be written as ϵ∼yN2/(yN1-yN2) (vev’s of the flavons are proportional to λΛ). So that, if yN2 was zero, the μ↔τ symmetry would be exact, then we assume that 𝜖 is small such that this parameter will be treated as a perturbation, thus, a pertubative study at first order in 𝜖 will be carried out. Therefore, we demand that |ϵ|≤0.3 as consequence quadratic (|ϵ|2) terms will be neglected.
As a result of having a diagonal charged lepton mass matrix, there is no contribution to the mixings, then the neutrino sector will provide it. To see this, we go back to the 𝐦 v mass matrix where m0ν is diagonalized by the following mixing matrixii
Hereafter, the superscripted in U0ν and the matrix elements m0αβ (α, β = e, μ, τ), denotes quantities when the μ ↔ τ symmetry is exact.
Going back to the expression ˆMν=u†νmνu*ν, then uν≈U0νUϵν which implies
In addition, we have
As we already commented, the parameter 𝜖 is considered as a perturbation so that the mixing matrix Uϵν is obtained by using perturbation theoryiii at first order in |ϵ|. Consequently, we obtain
where the normalization factors are written as
At last, the theoretical formulas for the mixing angles are obtained by comparing our PMNS mixing matrix, U≈U†eUν=U0νUϵν, with the standard parametrization, then we finally get
As one can realize if ϵ goes to zero, one would obtain the well known predictions: θ13=0, θ12=θ and θ 23= π/4.
In order to figure out the set of free parameter values, an analytical study on the theoretical formulas is carried out. It is important to note that the reactor angle depends strongly on the breaking parameter and the ratio among complex masses, m0i=|m0i|eiαi. In the former factor, the associated phase ϵ=|ϵ|eiαϵ is irrelevant however the difference m02-m01 and m01-m03 are crucial to enhance the reactor angle value, then CP parities values turn out being relevant to accommodate the reactor angle. As result of this, we choose the following CP parities values m02=-|m02|, m01=|m01| and m03=|m03|. To add to it, the solar and atmospheric angles are sensitive to the associated phase α 𝜖 and the CP parities values of the neutrino masses.
In the current analysis, the normal hierarchy is not favored as one can check straightforward, then we just focus in the inverted ordering. Due to the CP parities in the neutrino masses, we obtain
Let us consider two extreme cases where the lightest neutrino mass takes part. According to the squared mass scales Δm221=|m02|2-|m01|2 and Δm213=|m01|2-|m03|2, two neutrino masses might write as |m02|=√|m01|2+Δm221 and |m01|=√|m03|2+Δm213.
Strict inverted hierarchy (|m03|=0): In this case, we have |m01|=√Δm213 and
Then, one can obtain a precise values for the mixing angles
where rA=Δm221/2Δm213.
In the above expressions, we have considered sinθ=1/√3 which is a good approximation to the tribimaximal scenario [53-56], |ϵ|=0.3 and αϵ=0 we obtain sinθ13≈0.0234, sinθ12≈0.587 and sinθ23≈0.713. In the case where αϵ=π, the solar and atmospheric angles have similar values in comparison to above case.
Almost degenerate |m03|≫√Δm213: In this limit, we obtain the following masses
with rB≈Δm213/2|m03|2 and rC≈Δm221/2|m03|2.
For this reason, the mixing angles formulas are written as
Remarkably, in this scheme the three angles can be accommodated with great accuracy according to the experimental data as we will see later.
Before finishing this section, it is worthy of mentioning the relation among the reactor angle and the deviation of the solar and atmospheric angles, respectively. To do so, in the strict hierarchy case we have
then
In the almost degenerate case, one can write
subsequently
where the ± represents the π and 0 values for the αϵ phase.
2.3.2. Quark sector
As we already commented, the lepton sector was studied mainly in this paper. Then, we want to address briefly the quark sector within a particular benchmark as follows. We adopted the following alignments 〈H1〉=〈H2〉 which is consistent with the minimization of the scalar potential [49-51]. Hence, one gets
where q=u,d and the defined parameters can be read of Eq. (4). Let us remark that ℳ q has bee studied exhaustively in [52] and significant results were released. Nonetheless, we want to address the quark mass matrices in different way so that some assumption will be done. To do so, notice that ℳ q is diagonalized iv by Uq(L,R) such that Mq=U†qLMqUqR with Mq=Diag.(mq1,mq2,mq3) denoting the quark physical masses. Then, the following rotations is realized Uq(L,R)=Uπ/4uq(L,R) so that Mq=u†qLmquqR. Notice that
At this stage, two assumptions are made A q = 0 and C q = D q . To be honest, we could not eliminate the former entry by means the S4⊗Z2 discrete symmetry and the latter assumption might be realized within the left-right theory[57-60] by invoking parity symmetry. Also, as was shown in [37], the second assumption can be realized by a suitable transformation in the right-handed quarks fields (there are no right-handed currents in the model), which are SU(2)L singlets, such that the resultant quark mass matrix turns out being hermitian. Due to this fact, we could have assumed that ℳ q is hermitian but only the aforementioned simplification was carried out. In this benchmark the quark mass matrix has the generalized Fritzsch textures [37-39] which fit with great accuracy the CKM mixing matrix.
As a result, the CKM mixing matrix is given by V=U†uUd=OTuˉPqOd where ˉPq=P†uPd and the 𝐎 q orthogonal matrix has the following form
where q=u,d. In addition,
As we can show in the Appendix B, in the CKM matrix there are four parameters namely |Eq| (q = u, d) and two effective CP-violating phases (α and β) so that a numerical study will be realized to fix them.
3. Results
3.1. Lepton sector
We have shown that our theoretical formulas on the mixing angles can accommodate the experimental data where the inverted hierarchy is favored. In order to get a full set of free parameter values that fit the mixing angles, then some scattered plot will be elaborated as follows.
The mixing angles depend on three free parameters, explicitly
Hence, from the previous analytical study the three free parameters let vary on the following ranges: ϵ∈[-0.3,0], θ∈[0,π/3] and |m03|∈[0,0.09] eV. Therefore, we demand our theoretical formulas satisfy (at 3σ) the following values [4]
for the inverted hierarchy. Additionally,
Having included the experimental data, the scattered plots are constructed by using the theoretical formulas given in Eq. (16) which have to satisfy the experimental values. As a result, the mixing angles as function of the lightest neutrino mass are displayed in Fig. 1. The allowed region of values for the |m03| is consistent with the previous analytical study.
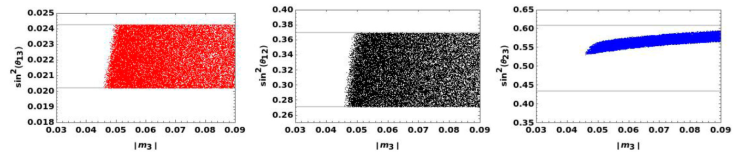
Figure 1 From left to right: the reactor, solar and atmospheric angles versus the |m03| lightest neutrino mass. The thick line stands for 3σ of C. L.
As it was already commented, the θ parameter is identified with the solar angle in the limit of μ↔τ exact. Then, the following scattered plots exhibit the region where θ parameter lies around the experimental value of the solar angle. In fact, this value is close to tribimaximal prediction since the solar angle receives a small correction from 𝜖.
In the previous analytical study, we showed the 𝜖 parameter must be negative and this may vary in the interval [0,-0.3]. The numerical study shows the favored region where the mixing angles are fitted at 3σ, see Fig. 3. Evidently, the case with |ϵ|=0 is excluded due to this stands for the limit of exact μ↔τ symmetry.
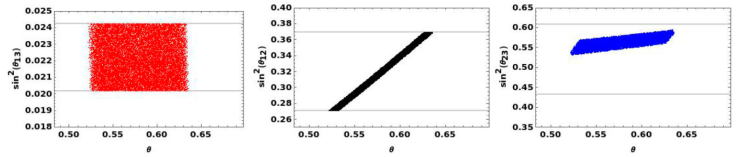
Figure 2 From left to right: the reactor, solar and atmospheric angles versus the θ parameter. The thick line stands for 3σ of C. L.
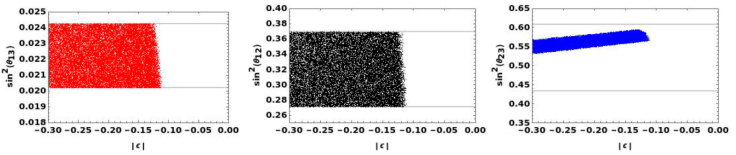
Figure 3 From left to right: the reactor, solar and atmospheric angles versus the |ϵ| parameter. The thick line stands for 3σ of C. L.
As model prediction, we have calculated numerical the effective Majorana mass of electron neutrino which is defined as follows
with m i represents the physical neutrino mass and Uei PMNS matrix elements. This effective mass has been measured by GERDA phase I[61] and II [62], and the lowest upper bound is |mee|<0.22 eV.
In our model, CP parities have been used in the neutrino masses. In particular, we utilized m02=-|m02|, m01=|m01| and m03=|m03| since this fit quite well the mixing angles. Consequently, the predicted region for the effective Majorana mass of electron neutrino is shown in the following scattered plots.
3.2. Quark sector
Our numerical study consists in making scattering plots. To do so, we compare our CKM theoretical expression with the standard parametrization one. In particular, we consider the entries (Vui)th (i=d,s,b) and (Vcb)th that depend on the free parameters
Therefore, we demand the magnitude of mentioned entries must satisfy the following experimental values [32]
In the current study, the physical quark masses are considered as input values. To be more precise, the normalized quark masses (mqi/mq3) will be used due to their ratios do not change drastically at different energy scales as one can verify directly from [63]. So that, at the top quark mass scale we have [22]
In addition, for simplicity, two dimensionless parameters have been defined yq≡|Eq|/mq3 (q = u, d), then we now have the constraint 1>yq>˜mq2≡|mq2|/mq3>˜mq1. Explicitly, for the up and down sector 1>yu>˜mc≡|mc|/mt>˜mu and 1>yd>˜ms≡|ms|/mb>˜md.
With all the above information, we calculate the allowed regions for the four CKM entries and constrain the free parameter set of values. However, let us show you only the scattered plots for |Vub| and |Vcb| since that these entries usually are complicated to fit. As we already commented the theoretical expression are required to satisfy the experimental data up to 3σ. Moreover, the normalized quark masses let vary up to 2σ and the two CP-violating phases are in the range [0,2π]. Then, as one notices, in Fig. 5, there is a set of values in which |Vub| is fitted with great accuracy.
Focusing in the dimensionless parameters yu and yd, the favorable regions lie in [0.5,1) approximately. Additionally, there are two regions of values for the CP phases, α and β, where the magnitude of |Vub| is accommodated. In the Fig. 6, we see |Vcb| as function of the four free parameters and these have the same allowed region as the above case.
To finish this section, we want to comment our naive analysis showed a large region of values for the free parameters where the theoretical CKM entries are in good agreement with the experimental data up to 3σ. A strict study, as for example an χ 2 fit, must determine better the space of values however the principal aim of this numerical study was shown the generalized Fritzsch mass textures fit the CKM matrix as it is well known.
4. Summary and conclusions
To sum up, we have built a non-renormalizable model where the fermion mixing is driven by the spontaneous breaking of the S4⊗Z2 discrete group. An appropriated alignment of the scalar vev’s allows to break the μ↔τ symmetry in the effective neutrino mass matrix. Therefore, under a perturbative study, we were able to correct the wrong predictions on the reactor and atmospheric angles, and a set of values for the free parameters was found such that the mixing angles are consistent with the latest neutrino data. Due to the lack of extra symmetries, in the quark sector, a benchmark allows to get consistent mass textures that accommodate the CKM mixing matrix.
We have learned that the flavor symmetries have been useful to eliminate spurious parameters in the Yukawa sector. At the same time, those shape the fermion mass matrices, consequently the mixing pattern can be obtained straightforwardly. Ambitious flavored models have gone beyond of fitting the mixings and prediction on some free parameters (Majorana phases, Dirac CP phase for instance) have been done. In conclusion, despite the μ↔τ is outdated, in this constrained model, we wanted to show you that a simple soft breaking is enough to correct the mixing angles. Although the model predictions are so limited and the favored inverted hierarchy goes against the data, a soft breaking of μ↔τ is still alive from theoretical point of view nevertheless the experiments have the verdict.











 nueva página del texto (beta)
nueva página del texto (beta)





