Appendix A

Derivation of Equation (9) in Detail

We start the formal derivation from equation (7)

For simplicity and tractability, let D =(I −hA) and g =(sf + e) , and write equation (A-1) as follows:

Equation (A-2) holds for any point in time with x, A, f, e, h and s. Then differencing (A-2) yields

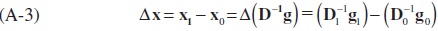
Equation (A-3) can be expressed in a way that each term on the right-hand side of the equation increases by the amounts of ΔD^-1 and Δg respectively between time 0 to time 1. We then obtain

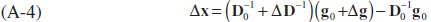
Upon expanding (B-4), we get

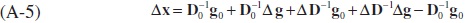
Cancelling out the similar terms, we finally derive the following expression:

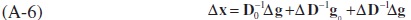
In calculating equation (A-6), it is quite important the way we handle the last interactive term (see Martin and Evans, 1981). Some similar studies in the literature recognise the presence of the last term, but none explicitly calculate it, preferring instead to calculate it as a residual. However, we here follow a different way. In the present context, we assume that either the first or the second term on the right hand side of (A-6) can compromise this last term. If the first term includes the last term, then equation (A6) become weighted by the terminal year of the structural D^-1 and the base year of the volume g, and vice versa if the this term is absorbed by the second one. This is rather similar to Paasche and Laspeyres index weightings respectively. Given this explanation, equation (A-6) respectively can be re-written as follows:

Despite the fact that the calculations using both weighting yield the analogous, we use the Laspeyres weighting for presentation. However, the same derivation can be repeated for the Paasche weighting. For our present purpose, the first term on the righthand side of (A-8) can be decomposed as follows:

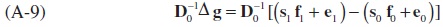
Adding and subtracting the term s₀ f₁ from the right-hand side of (A-9) yields:

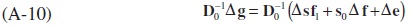
The second-term on the right-hand side of (A-8), on the other hand, can be decomposed as:

Since multiplying the first and the second term in the bracket on the right-hand side of (A-11) by (D₀^-1 D₀) and (D₁D₁^-1) does not change equation (A-11), the following can also be written:

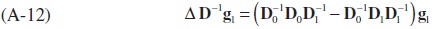
Upon re-written (A-12),

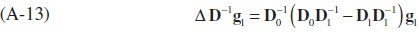
From (A-13), the following can also be derived:

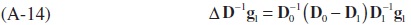
From equation (A-2), let D_{1⁻¹g1 = x1 and write (A-14) as follows:}

Substituting the definition of D₀ and D₁ in the (A-15) yields

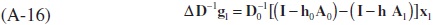
Re-arranging (A-16) gives us equation (A-17) below

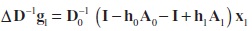
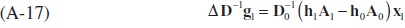
Adding and subtracting the same term h₀A₁ from (A-17),

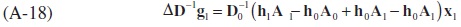
Re-arranging the resulting equation (A-18) gives,

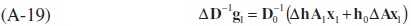
Finally substituting (A-10) and (A-19) into (A-8) yields the following:

Letting D₀ ^-1 = R₀ we can derive equation (9b) in the text:

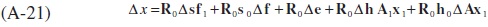
Using Paasche weighting the derivation of equation (9a) is also analogous to (A-21).