Anexo I

Derivación del portafolio óptimo en el modelo MTSL

La forma en que se determinó el portafolio óptimo W en el contexto del modelo MTSL y en la forma en que operó en el simulador programado parte de dos pasos fundamentales. El primero de ellos es la derivación del conjunto de portafolios que conforma geométricamente a la frontera eficiente ( ξ ), el cual tendrá una cardinalidad de 100. El segundo de ellos consiste, partiendo de una tasa de interés que paga un activo libre de riesgo rf, determinar cuál de los 100 miembros de if es el que maximiza la pendiente de la línea de asignación de capital o ratio de Sharpe. El primer paso se resuelve utilizando programación cuadrática empleando un algoritmo sugerido por Martin (1955), el cual utiliza métodos de optimización restringida con multiplicadores de Lagrange que permite satisfacer tanto las restricciones de no negatividad (exclusión de ventas en corto) como la restricción presupuestal que hace que w_k sea un vector de norma unidad.

Para lograr esto se resuelve la minimización de la función de varianza del portafolio, w_k, dado el nivel de rendimiento esperado E_k^* ∈ [min (r), max(r)] dado por E_k^* = e' · W_k. Esto es:

Este problema de optimización se presenta como sigue:

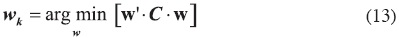
Sujeto a:

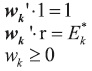
El mismo lleva al planteamiento de la siguiente ecuación lagrangeana:

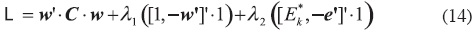
Dadas las condiciones de primer orden de (14), se llega al siguiente planteamiento matricial:

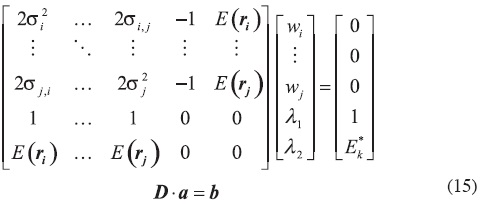
Dado que el vector a se forma del vector de multiplicadores de Lagrange y del vector de pesos W_k ( a = [w_k, λ₁, λ₂]'), se resuelve (15) y se observa cuáles elementos de W_k violan la restricción de no negatividad. Posteriormente, se eliminan de D, a y b en (15) las filas y columnas correspondientes al i-ésimo activo que incurre en dicha violación, se le asigna un valor de w_¡ =0 en el resultado final a ese activo y se resuelve el nuevo sistema planteado para (15) hasta lograr que todas las entradas del vector W_k cumplan con las restricciones dadas, lo que implica que algunos activos financieros tengan niveles de inversión de cero y se llegue incluso a colocar todo el balance de inversión en uno solo, situación que al no incorporar restricciones de cardinalidad en W_k deriva en un problema de concentración de activos observable en los resultados del presente estudio. Con la derivación de (15) para 100 valores de E_k ∈ [min (e), max (e)] , se deriva ζ. Los pasos anteriormete expuestos se realizaron en un algoritmo informático programado en MATLAB:

Algoritmo 1 para derivar W con el modelo MTSL:

Inicio

• Definir:

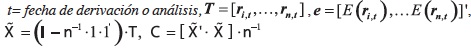
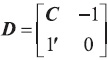con 1 y -1 de dimensión (2x1) y 0 de rango 2.

• Hacer para 100 diferentes valores de : E*_k ∈ [min(t?),max(e)]

■ Definir:

a=[w_k, λ₁, λ₂]' y b=]0',1,E^*_k]

• Determinar w_k ∈ a empleando (14): a = C^-1 . b

• Si w_k<0 , hacer mientras que encontrado=falso
∀ w_i ∈ w_k, w_i=0⇔w_i< 0
Eliminar i-ésimas columna y fila de C, a y b que verifican w_¡ < 0 .
Resolver w_k ∈ a empleando de nuevo (15): a = C^-1 ·b
Si w_k ≥ 0 ⇒ encontrado=verdadero
Se establece: w_k∈ ξ_t

• Determinar la definición de W_t por observación directa de los valores de S_ξ con (6):

• Determinar el ratio de Sharpe dado para W_t : S_W,t= (E_w —rf_t) · σ_ξ^-1
Fin

Anexo II

Lógica general del algoritmo empleado en el simulador programado.

El algoritmo que se utilizó para realizar las simulaciones de eventos discretos se programó, al igual que el previamente expuesto, en MATLAB y la lógica general y pasos realizados se exponen a continuación.

Algoritmo 2 para realizar la simulaciones de eventos discretos

Inicio

• Definir: t = 01 de febrero de 2001.

• Hacer mientras Condición de paro de Loop=falso:

o Definir ξ_t, W_t y S_W,t al realizar el Algoritmo 1 para derivar W con el modelo MTSL.

o Determinar vector niveles de inversión m por activo en definición de portafolio de mercado M_A .

o Calcular el ratio de Sharpe de M_A con (9):

o Si t=31 de diciembre de 2010 ⇒ Condición de paro de Loop = verdadero.

■  Si t ∈ [01 de febrero de2001,31 de diciembre del 2010]⇒ Condición de paro de Loop = falso

■ Definir t = fecha mensual y laborable siguiente a la actual.

• Contrastar gráficamente el conjunto de fronteras eficientes Ξ = {ξ} y valores de E_w,t σ_w,t, E_M,t, σ_M,t .

• Realizar prueba ANOVA unidireccional para contrastar S_M y S_w,t.

• Graficar los valores históricos de S_Ma y S_W,t .

o Si existen comportamientos o fluctuaciones atípicas en S_w,t ⇒ Segmentar las observaciones de S_Ma y S_W,t en periodos homogéneos atendiendo algún criterio preferentemente relacionado a los ciclos económicos.

■ Realizar de cuenta nueva la prueba ANOVA unidireccional para contrastar S_Ma y S_W,t en cada segmento temporal creado.

Fin