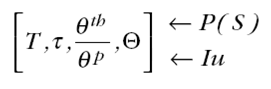Aleph
Matemáticas para la vida. Una propuesta para la profesionalización docente de profesores de matemáticas
Mathematics for life: a proposal for the professionalization of mathematics instructors
Resumen:
La sociedad espera que la formación matemática que tiene lugar en las escuelas dote a los ciudadanos de herramientas para enfrentar diversas situaciones y problemas de la vida actual. Para generar esta formación matemática, el profesor resulta un elemento fundamental. Por consiguiente, en este trabajo se presenta el curso de un programa de profesionalización docente en línea y a distancia, diseñado para proveer de herramientas teórico-metodológicas (de la Teoría Antropológica de lo Didáctico) a profesores latinoamericanos de matemáticas en servicio. Las cuatro actividades de este curso, realización, develación, diseño e implementación permitieron proponer una ruta para que los profesores diseñaran y adaptaran actividades didácticas para la vida. En este artículo se presenta a profundidad el análisis de las producciones de los profesores en la primera actividad del curso, en la cual se relaciona geometría y topografía. Esta actividad resulta crucial para que posteriormente se diseñen actividades similares.
Palabras clave::
Matemáticas para la vida, profesionalización docente, diseños didácticos
-
Sections-Introducción
Propuesta teórico-metodológica basada en elementos de la TAD
Diseño de una actividad para la vida que relaciona praxeologías topográficas con praxeologías geométrica
Un curso de profesionalización docente para el diseño de actividades que relacionan Pc con Pm
Análisis de las praxeologías topográficas-geométricas realizadas por profesores de matemáticas en el curso
Técnicas topográficas
Conclusiones
Referencias
Introducción
Una de las demandas para la enseñanza de las matemáticas, en la actualidad, es que los conocimientos matemáticos sean herramientas para abordar problemas y enfrentar situaciones de la vida (UNESCO, 2014; OECD, 2016). Sin embargo, se han evidenciado prácticas de enseñanza en las que el énfasis está en los conceptos y los saberes matemáticos, sin necesariamen- te comprender su contexto de origen o su relación y uso en otros contextos. Esto se ve reflejado, por ejemplo, en la enseñanza de la geometría que se ha centrado en el estudio de lo teórico, favoreciendo el estudio de la figuras geométricas y demostraciones, dejando el contexto de aplicación como una “vestimenta” de la actividad matemática a desarrollar (Covián, 2013; Lave, 1988). Dichas prácticas o enfoques didácticos son denominados por Chevallard (1992) como monumentalistas. Por lo que, uno de los cuestionamientos es cómo cambiar este enfoque hacia uno más abierto e innovador, en el que se explicite la razón de ser de la enseñanza de las matemáticas. Una de las rutas para generar este nuevo enfoque es a través de los profesores, que como menciona Artigue (2011,p. 7) “[…] son el elemento clave de toda evolución positiva y durable de los sistemas educativos. Constituyen hoy el reto principal de una educación matemática para todos”. Es decir, incidir en su desarrollo profesional es incidir en la formación de calidad de los futuros ciudadanos.
-
UNESCO, 2014Programas y Presupuesto Aprobados (37 C/5), 2014
-
OECD, 2016PISA 2015 Mathematics FrameworkPISA 2015 Assessment and Analytical Framework: Science, Reading, Mathematic and Financial Literacy, 2016
-
Covián, 2013La formación matemática de futuros profesionales técnicos en construcción, 2013
-
Lave, 1988La cognición en la Práctica, 1988
-
Chevallard (1992)Concepts fondamentaux de la didactique : Perspectives apportées par une approche anthropologiqueRecherches en didactique des mathématiques, 1992
-
Artigue (2011,p. 7)Les défits de l’enseignment de mathématiques dan l’education de base, 2011
En las últimas dos décadas se han desarrollado diversos programas de profesionalización docente con el objetivo de actualizar y enriquecer los conocimientos didácticos de los profesores (Tirosh, 2009). Una parte, todavía mínima, de estos programas son propuestos en la modalidad en línea y a distancia. Éstos conforman comunidades de formación y profesionalización, que permiten que los profesores generen discusiones y reflexiones profundas de su práctica, a través de la interacción con colegas de diferentes realidades educativas y con expertos en la investigación en didáctica (Scott y Scott, 2010). Sin embargo, hay muchas cuestiones todavía abiertas sobre las necesidades de los profesores y las formas en que los programas de este tipo las atienden. Algunas de ellas, son ¿Cómo acercar los múltiples resultados de la investigación en matemática educativa a los profesores? ¿Cómo lograr que las herramientas teóricas y metodológicas se vuelvan útiles para los profesores y les permitan generar una enseñanza de las matemáticas para la vida?
-
Tirosh, 2009What do we know about mathematics teacher education? What evidence do we have? What comes next?Journal Mathematics Teacher Education, 2009
-
Scott y Scott, 2010Innovations in the Use of Technology and Teacher Professional DevelopmentOnline Learning Communities and Teacher Professional Development: Methods for Improved Education Delivery, 2010
Considerando esta última pregunta, se ha diseñado un curso para un programa de profesionalización docente en la modalidad en línea y a distancia del Centro de Investigación en Ciencia Aplicada y Tecnologías Avanzada del Instituto Politécnico Nacional (CICATA-IPN), cuyo objetivo es proveer herramientas teóricas y metodológicas para que los profesores diseñen actividades didácticas para la vida. Se consideró que para poder elaborar este tipo de diseños primero es necesario analizar la actividad matemática tanto en contextos escolares como no escolares -de la vida-. Es decir, para estar en posibilidad de generar nuevas relaciones entre estos contextos a través de los conocimientos matemáticos. Se eligió como marco teórico la Teoría Antropológica de lo Didáctico (TAD), ya que ésta posee un modelo para el análisis de la actividad en su dimensión institucional (Chevallard, 1999).
-
Chevallard, 1999L’analyse des pratiques enseignantes en théorie anthropologique du didactiqueRechcerches en Didactique des Mathématiques, 1999
Esta comunicación consta de cinco secciones que se enuncian a continuación. En la primera, se presenta una propuesta teórico-metodológica basada en elementos de la TAD, que permite el diseño de actividades para la vida. En la segunda, se muestra el diseño de una actividad para la vida que relaciona conocimientos geométricos y topográficos. En la tercera, se presenta el diseño del curso implementado en el programa de profesionalización docente. En la cuarta, se presenta el análisis de las producciones de los profesores al realizar la actividad topográfica-geométrica y cómo esta vivencia incide de manera importante en los diseños didácticos que ellos generan en equipo, que se ilustran con dos ejemplos. Finalmente, en la sección cinco, se reportan las conclusiones de este trabajo.
Propuesta teórico-metodológica basada en elementos de la TAD
Esta investigación se enmarca en la Teoría Antropológica de lo Didáctico (TAD) que tiene un modelo para el análisis la actividad (actividad matemática, actividad topográfica) en su dimensión institucional. Particularmente se consideran tres de sus elementos: institución, praxeología y modelo praxeológico extendido. Las instituciones, según Castela y Romo (2011), son organizaciones sociales estables, que establecen normas y condiciones que restringen la actividad de los sujetos, pero al mismo tiempo la posibilitan, a través de recursos que ponen a su disposición. En esta investigación el interés está centrado en analizar conocimientos matemáticos en contextos escolares Ce y contextos extra-escolares (de la vida) Cv, vistos como instituciones que tienen sus propias condiciones y recursos. Podríamos decir que, en Ce la función principal del conocimiento matemático es su difusión a través de la enseñanza, mientras que en Cv, dependiendo el caso, la función principal es su uso para enfrentar o explicar situaciones. Para mostrar la utilidad de las matemáticas y las posibles razones de su enseñanza, se considera necesario establecer relaciones genuinas entre conocimientos matemáticos presentes en un determinado Ce con un determinado Cv. Para ello, es pertinente identificar y analizar estos conocimientos en cada uno de estos contextos. Y de manera más general, analizar las actividades en las cuales dichos conocimientos están involucrados, a través de la praxeología.
-
Castela y Romo (2011)Des Mathématiques A L’Automatique: Etude des effets de transposition sur la transformée de Laplace dans la formation des ingénieursRecherches en Didactique des Mathématiques, 2011
La praxeología está compuesta por dos bloques: técnico-práctico (T, τ ) y tecnológico-teórico ( θ , Θ ). Donde T es una tarea de cierto tipo, compuesta por una tarea t, que debe realizarse por una técnica τ justificada por una tecnología θ que permite producirla, validarla y justificarla a través de una teoría Θ . En resumen “toda actividad pone en obra una organización que puede escribirse [T/ τ / θ / Θ ] y que se llama praxeología u organización praxeológica” (Chevallard, 1992, p. 3). Una praxeología matemática escolar podría ser t: calcular la hipotenusa c de un triángulo rectángulo cuyos catetos miden 3 y 4 unidades. τ : c2 = (3)2 + (4)2 = 25, c = 5. θ: teorema de Pitágoras y Θ: trigonometría.
-
Chevallard, 1992, p. 3Concepts fondamentaux de la didactique : Perspectives apportées par une approche anthropologiqueRecherches en didactique des mathématiques, 1992
La praxeología también permite analizar actividades matemáticas en Cv, sin embargo, la tecnología no será únicamente matemática sino también de uso. Por ejemplo, cuando en albañilería (Cv) se busca garantizar la escuadra o ángulo recto en las esquinas de una habitación (tarea), se colocan 3 clavos en un lado y 4 en el otro, equidistantes y se comprueba que al unir sus extremos hay 5 unidades. Aunque la técnica se apoya en el teorema de Pitágoras, ciertos albañiles no lo conocen y validan la técnica de forma práctica, ya que “siempre” ha funcionado. Es decir, existen explicaciones, justificaciones y validaciones asociadas al uso de la técnica matemática. Para analizarlas, se considera el modelo praxeológico extendido (Castela y Romo, 2011) esquematizado en la figura 1.
-
Castela y Romo, 2011Des Mathématiques A L’Automatique: Etude des effets de transposition sur la transformée de Laplace dans la formation des ingénieursRecherches en Didactique des Mathématiques, 2011
Thumbnail
Figura 1
Modelo praxeológico extendido (Castela y Romo-Vázquez, 2011)
Modelo praxeológico extendido (Castela y Romo-Vázquez, 2011)
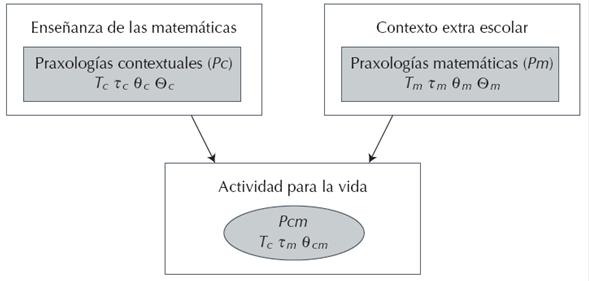
En éste, la tecnología tiene dos componentes uno teórico ( θ th ) y uno práctico ( θ p ). El componente práctico tiene seis funciones tecnológicas: describir, validar, favorecer, explicar, evaluar y justificar el uso de la técnica. Éstas, permiten analizar y evidenciar el tipo de validaciones que se producen al utilizar una técnica matemática para realizar una tarea (matemática o no) en un contexto no escolar. En este caso, P(S) es la disciplina matemática que produce y valida tecnologías matemáticas (como el teorema de Pitágoras) e Iu es una institución usuaria como la Albañilería o la Topografía. Con estos elementos teóricos es posible diseñar actividades para la vida (praxeologías didácticas) en las que se relacionen matemáticas escolares (praxeologías matemáticas o Pm) con matemáticas utilizadas en contextos extra-escolares (praxeologías contextuales Pc), ver figura 2.
Thumbnail
Figura 2
Elementos para el diseño de actividades para la vida
Elementos para el diseño de actividades para la vida
Para ilustrarlo, a continuación, se presenta el diseño de una actividad para la vida que relaciona praxeologías topográficas (Pc) con praxeologías geométricas (Pm).
Diseño de una actividad para la vida que relaciona praxeologías topográficas con praxeologías geométrica
En esta sección se presenta el diseño de una actividad topográfica-matemática, en torno al cálculo de áreas. Para su diseño se consideró y adaptó la metodología propuesta en Macias (2012) que consta de cuatro fases: la elección de un contexto extra-escolar, que en este caso es el topográfico; el análisis praxeológico para el cálculo de áreas en la topografía; el análisis praxeológico para el cálculo de áreas en la enseñanza de las matemáticas y el diseño de una actividad para la vida que relaciona praxeologías topográficas con praxeologías matemáticas. A continuación, describimos las últimas tres fases.
-
Macias (2012)Uso de las nuevas tecnologías en la formación matemática de ingenieros, 2012
Análisis praxeológico para el cálculo de áreas en la topografía
Se consideró el libro de difusión de la topografía de Pérez de Moya (1573), se identificaron dos praxeologías para el cálculo de áreas de terrenos “planos” y “no-planos” (P1 y P2), donde las técnicas y tecnologías involucran conocimientos geométricos.
-
Pérez de Moya (1573)Tratado de Geometría Prácticas y Especulativa. Observatorio de Marina de San Fernando y con licencia y privilegio Real de los Reinos de Castilla y Aragón, 1573
P1. Tipo de tarea 1
Determinar el área de un terreno “plano” (que carece de protuberancias o sinuosidades). Tarea 1. Determinar el área del terreno presentado en la figura 3.
Thumbnail
Figura 3
Terreno “plano” con forma irregular (Pérez de Moya, 1573, p. 185)
Terreno “plano” con forma irregular (Pérez de Moya, 1573, p. 185)
Técnica 1. La técnica se describe en Pérez de Moya (1573) de la siguiente forma:1
Situar el punto A (Figura 3), traza una línea al punto B y coloca una señal. Desde el punto B al punto C levanta una recta que forme un ángulo recto con AB y pon señales en cada uno. Luego, sitúate en el punto C y haz una línea al punto D y desde el punto D, una al punto A. De manera que, al final tengas un paralelogramo donde los lados menores tengan 8 y los lados mayores 12. Multiplica 8 por 12 y tendrás el área de la figura ABCD. Luego, para obtener lo demás haz en ellas cuadrados o paralelogramos o triángulos, la figura que quieras y sigue sus reglas. Para medir la figura IHKL, que por un lado tiene 3 cantidades, por otro 4, por otro 6 y por KH no se sabe qué cantidad. Pero, se puede encontrar el área. Suma 3 con 6 y será 9 toma la mitad (que es 4 y medio) y multiplícala por 4 y tendrás 18. Júntala con el área de la figura ABCD y de este modo irás midiendo las demás (Pérez de Moya 1573, p.85).
Tecnología θ th . Propiedades de las figuras conocidas (triángulos, cuadriláteros y circunferencias) y sus fórmulas para el cálculo de área, como se explicita “siguiendo la regla de la figura con la que la relacionarás” (Pérez de Moya, 1573, p.85).
-
Pérez de Moya, 1573, p.85Tratado de Geometría Prácticas y Especulativa. Observatorio de Marina de San Fernando y con licencia y privilegio Real de los Reinos de Castilla y Aragón, 1573
Tecnología θ p . Conocimiento del instrumento de medición usado, cinta o vara. La forma del terreno, irregular y “plano”, motiva el uso de ésta técnica (cercana al Método de Exhaución). La precisión en la medición y en el cálculo de áreas parece motivar las técnicas geométricas, así como la elección del instrumento.
Esto se hace más evidente en la siguiente praxeología de un terreno “no plano” porque tiene lagos o espacios de agua.
P2. Tipo de tarea 2
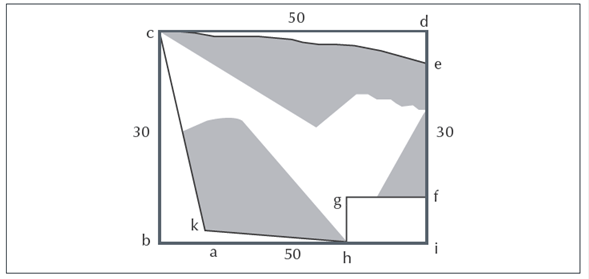
Determinar el área de un terreno “no plano” (con protuberancias o sinuosidades). Tarea 2. Determinar el área del terreno irregular con un lago en el centro, presentado en la figura 4.
Thumbnail
Figura 4
Terreno “no plano” con forma irregular (Pérez de Moya, 1573, p. 186)
Terreno “no plano” con forma irregular (Pérez de Moya, 1573, p. 186)
Técnica 2. Se describe primero una técnica general. “Se hará un paralelogramo o cuadrado circunscrito a tal terreno. Después de medido este cuadrado o paralelogramo se restará lo que vieres con lo que mide.” (Pérez de Moya, 1573, p. 186). Para facilitar la explicación de la técnica se da un ejemplo:
-
Pérez de Moya, 1573, p. 186Tratado de Geometría Prácticas y Especulativa. Observatorio de Marina de San Fernando y con licencia y privilegio Real de los Reinos de Castilla y Aragón, 1573
Como si fuese un pedazo de tierra que contenga una laguna de agua, de tal manera que se denota la figura abcd (Figura 4), haz un paralelogramo colocando tu instrumento a la redonda de manera que quede dcbi (Figura 5). Supongamos que este paralelogramo que circunscribe o abarca la tierra tiene por un lado 50 tamaños (sean varas o palos o lo que quieras) y por el otro 30. Mídela con tu regla y será 1500 y tantos tamaños o cantidades cuadradas. Mide después por la regla del triángulo la cantidad que hay entre la línea bc y el final de la tierra akc y lo que vieras entre kah y entre ihgf y entre edc. Lo que obtuvieras de restar con el paralelogramo y lo que queda, será el área de dicha tierra y de este modo se medirá cualquier otra forma. (Pérez de Moya, 1573, p. 186)
Thumbnail
Figura 5
Técnica para medir el área de un terreno “no plano” con forma irregular (Pérez de Moya, 1573, p. 186)
Técnica para medir el área de un terreno “no plano” con forma irregular (Pérez de Moya, 1573, p. 186)
Tecnología θ th . Propiedades de los paralelogramos, ángulos interiores rectos y lados opuestos iguales. La fórmula para calcular el área de triángulos.
Tecnología θ p . La tecnología práctica que motiva el uso de la técnica es la forma y tipo del terreno, irregular y que tiene lagos o espacios de agua; así como el uso que se dé a éste. Elección de puntos estratégicos para medir sin interferencia del lago.
La longitud y unidad de medida depende del lugar donde se efectúe la medición, como se ilustra en la siguiente cita: “Y por qué para medir de un modo u otro he puesto regla, no me detengo en ello, ni quiero decir otra cosa, sino que en uno y otro el Geómetra guarde la unidad del pueblo donde trabaje.” (Pérez de Moya, 1573, p. 186).
-
Pérez de Moya, 1573, p. 186Tratado de Geometría Prácticas y Especulativa. Observatorio de Marina de San Fernando y con licencia y privilegio Real de los Reinos de Castilla y Aragón, 1573
En estas dos praxeologías aparecen dos tipos de tareas no matemáticas, medir y calcular el área de terrenos planos y de terrenos con lagos o ríos en su interior. Las técnicas son matemáticas y topográficas (como el tipo de instrumento para hacer la medición). La unidad de medida aparece como un elemento clave, ya que en la época no existía una común a los diferentes pueblos. A pesar de que estos elementos, parecen no tener vigencia hoy en día, se considera que la búsqueda de precisión puede ser clave en un diseño didáctico y que los softwares de geometría (como Geogebra) pueden simular condiciones de terrenos para motivar técnicas geométricas sofisticadas.
Análisis praxeológico para el cálculo de áreas en la enseñanza las matemáticas
Se analizaron praxeologías matemáticas en libros de educación media superior (Fuenlabrada, 2007; Velasco, 2010; Zamora, Vázquez y Sánchez, 2007; Zúñiga, Zúñiga, y Zúñiga, 2012). En la mayoría se identificaron tareas para el cálculo de áreas de figuras “conocidas” (triángulos, cuadriláteros o circunferencias) y polígonos irregulares compuestos por estas figuras. Las técnicas predominantes favorecen el cálculo a través de la aplicación de fórmulas y la validación estaba relacionada con el uso ade- cuado de dichas fórmulas. Sin embargo en Zamora, et al. (2007) se identificó la praxeología para el cálculo de área de la Ciudad de México. Tarea no matemática justificada con técnicas mate- máticas pero con validaciones (tecnología) de naturaleza topográfica.
-
Fuenlabrada, 2007Geometría y Trigonometría, 2007
-
Velasco, 2010Geomtería y Trigonometría, 2010
-
Zamora, Vázquez y Sánchez, 2007Matemáticas 2: Geometría y Trigonometría, 2007
-
Zúñiga, Zúñiga, y Zúñiga, 2012Geometría y Trigonometría: Formación basada en competencias, valores y desarrollo de secuencias didácticas, 2012
-
Zamora, et al. (2007)Matemáticas 2: Geometría y Trigonometría, 2007
P3. Tipo de Tarea 3.
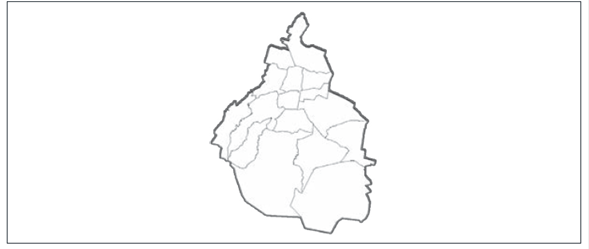
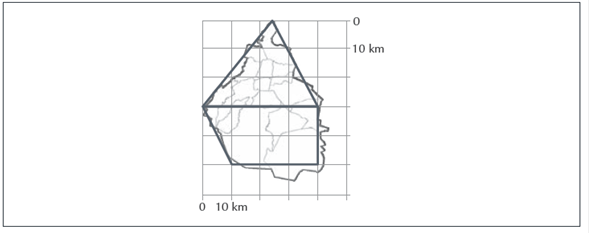
Calcular el área de terrenos irregulares. Tarea 3. Calcular el área de la Ciudad de México, dado su mapa (Figura 6).
Thumbnail
Figura 6
Mapa de la Ciudad de México (Zamora et al., 2007, p.103)
Mapa de la Ciudad de México (Zamora et al., 2007, p.103)
Técnica 3. En Zamora, et al. (2007), se presenta una técnica en tres partes, a, b y c, como se muestra a continuación:
-
Zamora, et al. (2007)Matemáticas 2: Geometría y Trigonometría, 2007
-
Datos: el mapa puede inscribirse en una figura geométrica.
-
Análisis: en primera instancia, intentaremos acotar el contorno de la figura geométrica que nos permita calcular el área correspondiente. Observemos que de las tres figuras (Figura 7) el heptágono irregular es el que se aproxima con menos error al área del mapa de la ciudad. Si triangulamos el polígono, sabemos que por ser heptágono debe contener (n - 2) triángulos, es decir: 7 - 2 = 5 triángulos. Podemos afirmar que la suma de las áreas de los cinco triángulos es aproximadamente igual al área de la Ciudad de México. Área del Heptágono = T1 + T2 + T3 + T4 + T5 = Área del mapa de la Ciudad de México.
-
Síntesis interpretativa: observa que los triángulos son diferentes, por tanto, el resultado implica obtener el área respectiva de cada uno de ellos. (Zamora et al. 2007, p. 104).
-
Zamora et al. 2007, p. 104Matemáticas 2: Geometría y Trigonometría, 2007
Thumbnail
Figura 7
Selección de la figura geométrica que se aproxima al área del mapa de la Ciudad de México (Zamora et al., 2007, p. 104)
Selección de la figura geométrica que se aproxima al área del mapa de la Ciudad de México (Zamora et al., 2007, p. 104)
Esta técnica puede reconocerse como matemática y topográfica, ya que se circunscribe a la figura, polígonos que permitan “encerrarla” de la mejor manera, como se propone en P2. Esto permite en un segundo momento triangular y calcular el área.
Tecnología θ th . Cálculo de área de figuras irregulares a partir de una descomposición en figuras regulares conocidas y sus fórmulas.
Tecnología θ p . Lo que motiva la técnica realizada es la aproximación de una figura lo más parecida al contorno de la figura de la Ciudad de México.
Esta praxeología se conforma de una tarea no matemática, elaborada a través de una técnica matemática cuya validación es matemática. Sin embargo, aunque no se presenta en la explicación del libro, la justificación práctica está basada en el grado de aproximación, elemento determinante en P1 y P2. Una vez identificados estos elementos (la unidad de medida, la asignación de medidas arbitrarias, el instrumento de medición y la búsqueda de proximidad) se procede a diseñar una actividad didáctica.
Diseño de una actividad para la vida que involucra tareas geométricas y topográficas.
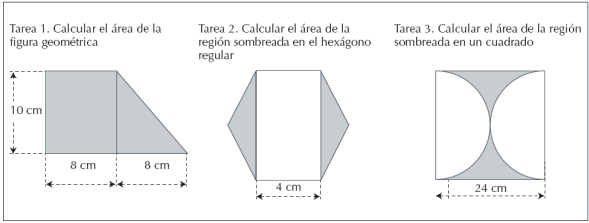
La actividad propuesta tiene seis tareas, geométricas y topográficas-geométricas, propuestas en un orden que permita a los profesores reconocer la riqueza de la actividad matemática de las tareas topográficas-geométricas. Así, las primeras tareas provienen de la enseñanza de la geometría, tienen formas conocidas, valores y unidades de medida asignadas.
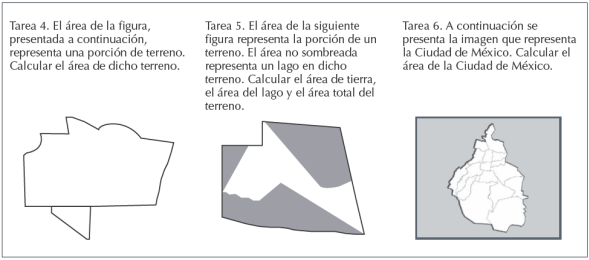
Las tareas 4, 5 y 6 son tareas topográficas basadas en P1, P2 y P3. En cada tarea se representa un terreno particular y para cada uno de pide calcular el área.
Como se observa, los dibujos presentados para las tareas 4 y 5 (figura 9) se basan en los terrenos representados en P1 y P2. Pero, se omiten los “datos”, como puntos de referencia (letras), unidades de medida y dimensiones. El dibujo de la tarea 6 se toma tal cual de P3.
En las tareas 1, 2 y 3 se solicitan técnicas matemáticas con validaciones (tecnologías) geométricas: conocimiento de las propiedades de las figuras y uso adecuado de las fórmulas. Mientras que las tareas 4, 5 y 6 poseen datos que caracterizan el terreno (planos, no planos, irregulares o forma de una ciudad conocida) más que una figura geométrica, lo que solicita el uso de técnicas sofisticadas y creativas que involucren elementos geométricos. La validación está asociada al grado de aproximación que se busque, entre mayor sea, la técnica más sofisticada será. Las potencialidades de estas últimas tres tareas, como se puede ver, están asociadas a una actividad matemática mucho más rica cercana a la matemática para la vida, pues para su realización requiere tanto de conocimientos geométricos, como de creatividad y de reflexión; de un trabajo autónomo y de capacidad para adaptar conocimientos conocidos a tareas nuevas, así como generar validaciones más allá de las matemáticas (precisión asociada al instrumento y a la unidad de medida). Se considera que, para acercar estas tareas y sus potencialidades a los profesores de matemáticas, es necesario que éstos las realicen y a partir de esta experiencia y de sus conocimientos profesionales puedan, en un segundo momento adaptarlas o implementarlas con sus estudiantes. Para ilustrarlo, se muestra a continuación un curso de profesionalización docente, donde la primera actividad es ésta del cálculo de áreas que involucra geometría y topografía.
Un curso de profesionalización docente para el diseño de actividades que relacionan Pc con Pm
Se diseñó un curso para el primer semestre (de la generación 2014-2016) de la maestría en Matemática Educativa del CICATA-IPN, la cual, está dirigida a profesores de matemáticas en servicio, en la modalidad en línea y a distancia. Los profesores participantes, de primaria hasta profesional, fueron 13 en total (9 mexicanos, 2 uruguayos y 1 paraguayo). El objetivo principal, en el curso, era proporcionar herramientas (presentadas en la sección 2 de esta comunicación) para el diseño de actividades didácticas para la vida que involucran relaciones entre Pc y Pm. El curso tuvo cuatro actividades, una por semana, que se detallan a continuación:
Thumbnail
Figura 8
Dibujos de las tareas 1, 2 y 3 de la Actividad 1
Dibujos de las tareas 1, 2 y 3 de la Actividad 1
Thumbnail
Figura 9
Dibujos de las tareas 4, 5 y 6 de la Actividad 1
Dibujos de las tareas 4, 5 y 6 de la Actividad 1
Develación de los elementos teórico-metodológicos que sustentan la actividad para la vida (Actividad 2). Se les devela, a los profesores, los elementos teóricos y metodológicos que sirvieron para diseñar la actividad realizada. Para ello, se solicitó la lectura y análisis del artículo (Covián y Romo, 2014), en el cual, se presenta un análisis praxeológico de la construcción de la vivienda maya y del levantamiento y trazo topográfico en la cultura egipcia. En ambos contextos se utilizan conocimientos matemáticos, como son la medida de la inclinación, la proporcionalidad, el teorema de Pitágoras y la construcción de figuras geométricas. Para guiar su análisis se propusieron preguntas del tipo: ¿qué conocimientos matemáticos aparecen en el análisis de construcción de la vivienda maya?, ¿estos conocimientos son objeto de enseñanza?, ¿en qué nivel?, ¿consideras que podría proponerse una actividad didáctica basada en el análisis de la construcción de la vivienda maya?, ¿tendría sentido?
-
Covián y Romo, 2014Modelo Praxeológico Extendido una Herramienta para Analizar las Matemáticas en la Práctica: el caso de la vivienda Maya y el levantamiento y trazo topográficoBolema, 2014
Diseño de una actividad para la vida (Actividad 3). Se solicitó a los profesores trabajar en equipo y diseñar una actividad didáctica. Esta actividad debía contener dos o más tareas que involucraran al menos un uso de cierto tema matemático. Es decir, hacer aparecer una utilidad actual de las matemáticas, y en cierta medida, real para los estudiantes. Para presentar su diseño, los profesores debían considerar al menos seis aspectos: tema matemático, utilidad de la enseñanza de este tema, nivel educativo, objetivos de la actividad, material necesario y la actividad didáctica.
Implementación de la actividad para la vida diseñada (Actividad 4). Se solicitó implementar la actividad diseñada (Activi- dad 3), a un grupo de estudiantes (pequeño grupo de voluntarios o bien a su clase). Esto para que ellos tuvieran una validación experimental de la actividad diseñada.
Estas cuatro actividades en su conjunto debían permitir a los profesores diseñar una actividad que involucrara un contexto de la vida (extra-escolar) y experimentarla con estudiantes. Este tipo de diseños están asociados a la complejidad de comprender la lógica del contexto considerado y la forma en que los conocimientos matemáticos se relacionan con otro tipo de conocimientos (prácticos, contextuales). Debido a esta gran complejidad, se considera que la Actividad 1 del curso resulta crucial para “convencer” a los profesores de que el diseño de actividades para la vida es sumamente importante y necesario para formar ciudadanos capaces de utilizar eficazmente las matemáticas en su vida. Para ilustrar este rol crucial de la Actividad 1, se presenta a detalle su análisis en la siguiente sección.
Análisis de las praxeologías topográficas-geométricas realizadas por profesores de matemáticas en el curso
Los profesores generaron una gran diversidad de técnicas para las tareas 4, 5 y 6 de la Actividad 1 del curso: trazo de figuras conocidas, cuadriculación de figuras, técnica mixta (fusión de las dos anteriores), trazo de un polígono sobre la figura utilizando un software y técnicas topográficas. La búsqueda de una “buena” aproximación fue un factor determinante para justificar, controlar y validar las técnicas. Para mostrar la riqueza de las técnicas y el rol de la precisión, se presenta a continuación el análisis del trabajo de 10 de los profesores, debido a que fueron los que presentaron con más detalle sus resoluciones y justificaciones.
Trazo de figuras conocidas
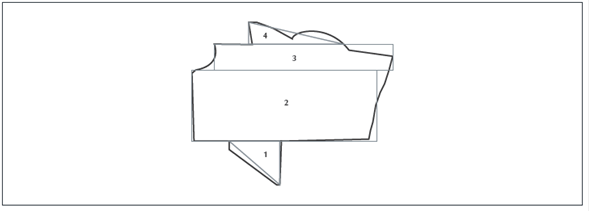
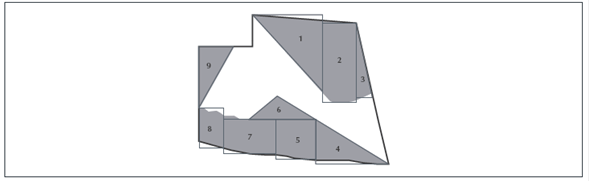
Para calcular el área del terreno plano (tarea 4), algunos profesores optaron por técnicas similares a las presentadas en P1. Insertaron figuras (triángulos o rectángulos) que abarcaran la mayor área posible. Seguido, insertaron figuras como triángulos y trapecios que también abarcaran el máximo de área restante y así sucesivamente. Luego calcularon el área de cada figura y las sumaron para obtener el total (figuras 10 y 11).
Thumbnail
Figura 10
Técnica de trazo de figuras conocidas en terreno plano por Karla
Técnica de trazo de figuras conocidas en terreno plano por Karla
Thumbnail
Figura 11
Técnica de trazo en figuras conocidas en terreno plano por Santiago
Técnica de trazo en figuras conocidas en terreno plano por Santiago
Ambos profesores buscaban una “buena” aproximación, como se ilustra en las descripciones que hacen sobres sus técnicas. Karla señala: “El resultado sería una aproximación. Si quisiera una buena aproximación entonces lo que haría es trazar una mayor cantidad de polígonos para tratar de cubrir mejor el área en cuestión”. Santiago demás explicita la escala como elemento que facilita la precisión: “El área de la figura es aproximadamente 18.62 cm2. El área aproximada de la porción de terreno dependerá de la escala empleada para realizar dicha figura”. Sin embargo, estos profesores usan nuevamente sus técnicas (1 y 2) en tareas donde ya no son óptimas. Karla privilegia el uso de rectángulos (ver figuras 12 y 13), lo que impide una buena aproximación, particularmente en el cálculo del área de la Ciudad de México. No investiga esta área, ya conocida 1.485 km2, lo que le impide buscar otra técnica, que resulte más precisa.
Thumbnail
Figura 12
Técnica de trazo de figuras conocidas en terreno con lago por Karla
Técnica de trazo de figuras conocidas en terreno con lago por Karla
Thumbnail
Figura 13
Técnica de trazo de figuras conocidas para calcular el área de la Ciudad de México por Karla
Técnica de trazo de figuras conocidas para calcular el área de la Ciudad de México por Karla
Thumbnail
Figura 14
Técnica de trazo de figuras conocidas en terreno con lago por Santiago
Técnica de trazo de figuras conocidas en terreno con lago por Santiago
Thumbnail
Figura 15
Técnica de trazo de figuras conocidas para calcular el área de la Ciudad de México por Santiago
Técnica de trazo de figuras conocidas para calcular el área de la Ciudad de México por Santiago
Entre mayor sea la aproximación buscada, se dibujaría un mayor número de polígonos conocidos, los más adecuados a la forma del terreno. Es decir, la precisión es una tecnología que regula y controla técnica, lo que se confirmará en las otras técnicas como se muestra a continuación.
Cuadriculación de figuras
Esta técnica consiste en sobreponer una cuadrícula o “rejilla” sobre la figura considerada, contar los cuadritos y determinar el área. La colocación de la “rejilla” se hace manualmente (a lápiz y papel) o con programas computacionales, como GeoGebra, Paint o Word.
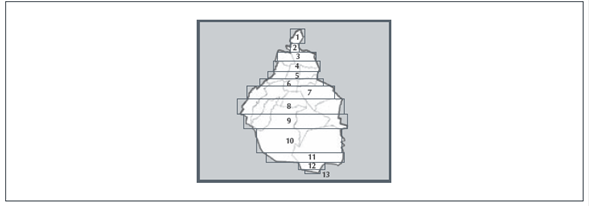
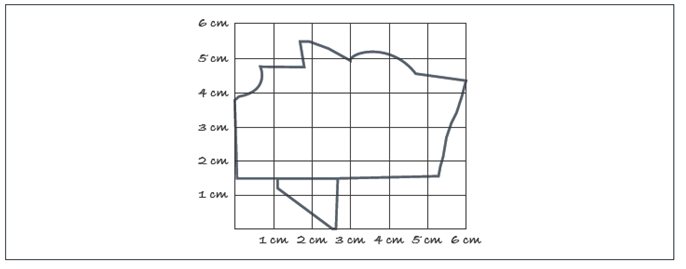
La cuadriculación manual la utilizan sólo dos profesores Alfonso y Horacio. Alfonso establece como unidad de medida 1 cm2 y determina un área de 21 cm2 para el terreno plano y un área total de 24 cm2 para el terreno con lago, donde 15 cm2 corresponden a la tierra firme (ver figuras 16 y 17). Horacio utiliza esta misma técnica para el cálculo del área de la Ciudad de México, el papel milimétrico es un medio que le permite obtener diferentes unidades de medida y por tanto determinar una mayor o menor aproximación (ver figura 18)
Thumbnail
Figura 16
Técnica de cuadriculación para terreno plano por Alfonso
Técnica de cuadriculación para terreno plano por Alfonso
Thumbnail
Figura 17
Técnica de cuadriculación para terreno con lago por Alfonso
Técnica de cuadriculación para terreno con lago por Alfonso
Thumbnail
Figura 18
Técnica de cuadriculación para calcular el área de la Ciudad de México por Horacio
Técnica de cuadriculación para calcular el área de la Ciudad de México por Horacio
[…] haciendo alarde de buena vista y concentración se procede a contar los “cuadritos” realizando ajustes en el caso de los bordes. Es decir, contar 2 por 1 o incluso 3 por 1, dependiendo del porcentaje ocupado. Cabe mencionar que, al realizarlo con otras personas, alumnos voluntarios, se obtuvo una medida de 593 a 600 unidades cuadradas o 5.93 a 6.00 cm2. (Extracto de reporte de Horacio, p. 3).
Para tener una mayor precisión, tres profesores usaron esta misma técnica, pero apoyándose en el uso de un software que permite ajustar la unidad de medida de área (cada cuadro).
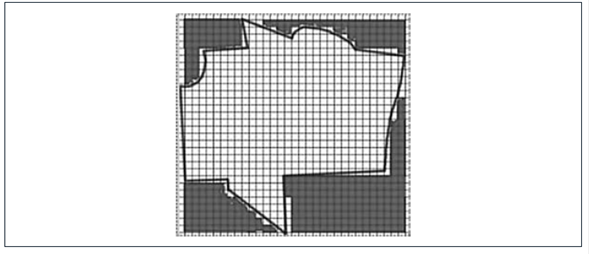
En el caso de María (figura 19), aunque no hizo el cálculo, la búsqueda de precisión está presente en su justificación, al mencionar que se pueden hacer aproximaciones al área por exceso (asignando cuadros grandes) o por defecto (dividiendo los cuadros grandes en cuadros cada vez más pequeños). En contraste César y Juan Pablo sí hacen los cálculos y determinan que el área del terreno plano es de 130 u2 y 2008.51 mm2, respectivamente (ver figuras 20 y 21). César considera la forma del terreno y en los bordes de la figura decide contar los cuadros como la mitad de la unidad considerada, mientras que Juan Pablo disminuye el tamaño de la unidad cuadrada de área para alcanzar una mayor precisión.
Thumbnail
Figura 19
Técnica de cuadriculación para terreno plano por María
Técnica de cuadriculación para terreno plano por María
Thumbnail
Figura 20
Técnica de cuadriculación para terreno plano por César
Técnica de cuadriculación para terreno plano por César
Thumbnail
Figura 21
Técnica de cuadriculación para terreno plano por Juan Pablo
Técnica de cuadriculación para terreno plano por Juan Pablo
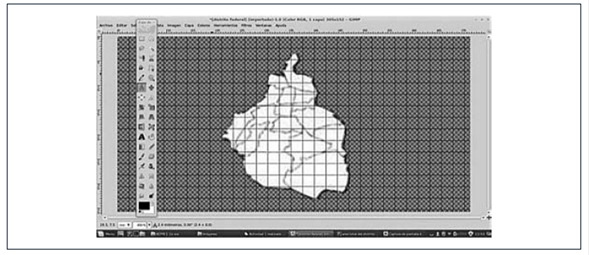
Esta misma técnica las adaptan César y Juan Pablo para obtener el área de la Ciudad de México (Figuras 22 y 23) con 1 mm2 de unidad.
Thumbnail
Figura 22
Técnica de cuadriculación para calcular el área de la Ciudad de México por César
Técnica de cuadriculación para calcular el área de la Ciudad de México por César
Thumbnail
Figura 23
Técnica de cuadriculación para calcular el área de la Ciudad de México por Juan Pablo
Técnica de cuadriculación para calcular el área de la Ciudad de México por Juan Pablo
En particular, se observó que el trabajar con una imagen “conocida” los llevó a cuestionar la precisión de su técnica. César menciona
[…] del conteo resultan 297 unidades de 4 km2, esto es, un total de 297 × 4 = 1 188 km2. Al final, el método tuvo sus deficiencias, puesto que el área de la Ciudad de México, según diversas fuentes, fluctúa entre 1 485 y 1 499 km2. (Extracto de reporte de César, p. 5)
Juan Pablo justifica el valor obtenido, considerando que no se calcula el área de los relieves presentes en la ciudad, lo cual es una justificación que tiene sentido al considerar el contexto “real” de la tarea:
Área calculada igual a 451 584 km2. Donde se da la escala de 1 mm2:1 km2. Se hace notar aquí que esto no corresponde a la superficie de la Ciudad de México, pues faltan los relieves del terreno. Lo que se calculó de manera aproximada fue entonces la superficie plana de la Ciudad de México. (Extracto de reporte de Juan Pablo, p. 4)
Se nota cómo el tipo de terreno juega un rol fundamental en la elección y refinamiento de la técnica, pero también el contexto “real”, particularmente de la Ciudad de México, permite contrastar el valor obtenido con el valor real de área. Efectuar el cálculo de área deja de ser una técnica únicamente geométrica y por tanto que tiene justificarse de acuerdo al contexto, como es el considerar montañas, cerros y relieves que también tienen una superficie.
Técnica Mixta
La técnica que se ha denominado Mixta es una “fusión” entre las dos técnicas analizadas previamente. Primero se cuadricula la figura, luego se insertan figuras geométricas conocidas (triángulos y rectángulos principalmente), se cuentan los cuadros en cada figura geométrica y se suman. Dos profesores usan software, mientras que Horacio vuelve a utilizar el papel milimétrico (ver figuras 24, 25 y 26).
Thumbnail
Figura 24
Técnica mixta en terreno plano por Carmen
Técnica mixta en terreno plano por Carmen
Thumbnail
Figura 25
Técnica mixta en terreno con lago por María
Técnica mixta en terreno con lago por María
Thumbnail
Figura 26
Técnica mixta en terreno plano por Horacio
Técnica mixta en terreno plano por Horacio
Carmen hace el cálculo de área “por compensación”, y describe la técnica así:
Considero que la zona del terreno que no quedó coloreada compensa aproximadamente los sobrantes que tengo en el polígono rojo y en el polígono celeste. Por lo que el área del terreno es aproximadamente la suma de las áreas de los polígonos rojo, violeta y celeste. La cuadrícula tiene relación 1:1.
El área de cada cuadradito es de 1 unidad cuadrado. Polígono rojo medio: 46 unidades cuadrado. Polígono rojo: 12 unidades cuadrado. Polígono rojo claro: 4 unidades cuadrado. El área del terreno es aproximadamente 62 unidades cuadro (Extracto del reporte de Carmen, p. 5)
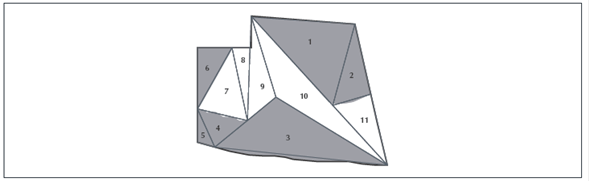
Se resalta que no utiliza “unidades cuadradas” sino unida- des cuadrado, que muestran claramente lo que representa el área calculada (62 unidades cuadrado). Por su parte, Horacio presentó un procedimiento que busca mayor precisión: estableció una unidad de medida (1 cm2) e insertó cuatro rectángulos, siete triángulos y una sección de círculo en la figura procesada (ver figura 26). María traza triángulos sobre tierra firme y cuenta los cuadros (ver figura 25). Esta técnica fue también utilizada para calcular el área de la Ciudad de México, asumiendo que esta tarea es del mismo tipo que la anterior: calcular el área de un terreno plano, pero con un contorno más irregular. Lamentablemente, para ellos el contexto “real” es obviado (ver figuras 27, 28 y 29).
Thumbnail
Figura 27
Técnica mixta para calcular el área de la Ciudad de México por Carmen
Técnica mixta para calcular el área de la Ciudad de México por Carmen
Thumbnail
Figura 28
Técnica mixta para calcular el área de la Ciudad de México por Julio César
Técnica mixta para calcular el área de la Ciudad de México por Julio César
Thumbnail
Figura 29
Técnica mixta para calcular el área de la Ciudad de México por María
Técnica mixta para calcular el área de la Ciudad de México por María
Trazo de un polígono sobre la figura con el apoyo de un software
Esta técnica consiste en trazar un polígono sobre la figura la figura de terreno plano y del terreno con un lago, apoyándose en la ayuda de un software (GeoGebra o Free Map Tool) que tiene herramientas para el cálculo de áreas. Una cuestión que apareció fue la preservación de la escala al escanear y procesar la imagen. Los profesores buscaron que el cálculo obtenido mediante el software fuera realmente el de las figuras “originales”. Esta técnica fue presentada por los profesores Gilberto, Alfonso y Julio César. A continuación, se ilustran las dos primeras (ver figuras 30 y 31).
Thumbnail
Figura 30
Técnica de trazo de un polígono en terreno plano por Gilberto
Técnica de trazo de un polígono en terreno plano por Gilberto
Thumbnail
Figura 31
Técnica de trazo de un polígono en terreno con lago por Alfonso
Técnica de trazo de un polígono en terreno con lago por Alfonso
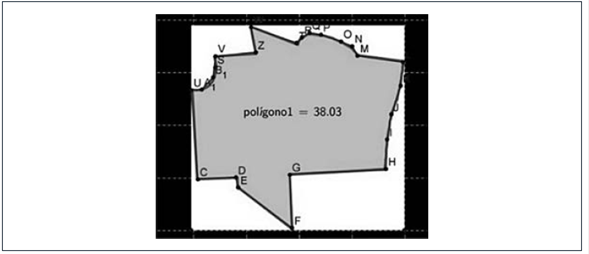
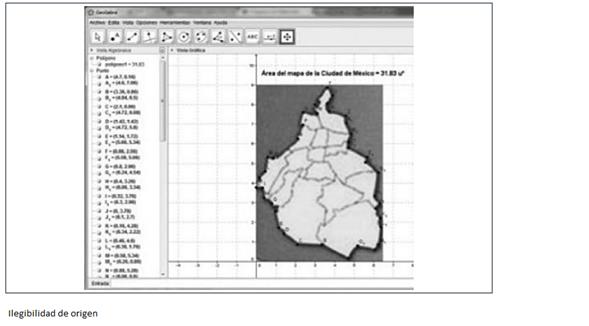
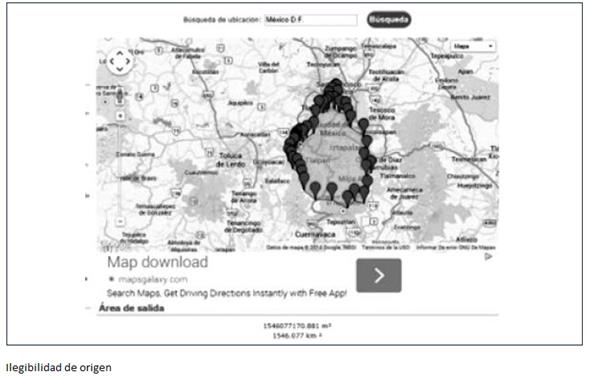
Dado que el software permite el trazo de polígonos con gran cantidad de lados, entonces “un polígono con mayor número de lados” asegura “mayor precisión en el cálculo del área”. Esto se ilustra particularmente bien en las técnicas presentadas por Alfonso y Julio César para el cálculo del área de la Ciudad de México. Alfonso utilizó GeoGebra y obtuvo el valor del área. Julio César investigó en la red y ubicó el software Free Tool Maps, en éste es posible pedir la representación del mapa de cualquier ciudad, por lo que él solicitó el de la Ciudad de México, luego insertó un polígono y obtuvo el valor del área con un error de 61 077 km2 con respecto al valor “real”. Aunque él explicita en su reporte que, si dibujaba polígonos con mayor número de lados, obtendría una mejor aproximación, no lo hizo. Un trabajo sobre este software permitió corroborar que efectivamente es posible hacer cálculos con mayores aproximaciones.
Thumbnail
Figura 32
Técnica de trazo de un polígono para calcular el área de la Ciudad de México por Alfonso
Técnica de trazo de un polígono para calcular el área de la Ciudad de México por Alfonso
Thumbnail
Figura 33
Técnica de trazo de un polígono para calcular el área de la Ciudad de México por Julio César
Técnica de trazo de un polígono para calcular el área de la Ciudad de México por Julio César
Técnicas topográficas
Las dos técnicas presentadas a continuación, cálculo de áreas por medio de coordenadas rectangulares y el cálculo de áreas por medio de la inscripción de círculos, son topográficas, puesto que son usadas en Topografía para determinar el área de terrenos delimitados por polígonos o poligonales “muy irregulares”.
Cálculo de áreas por medio de coordenadas rectangulares
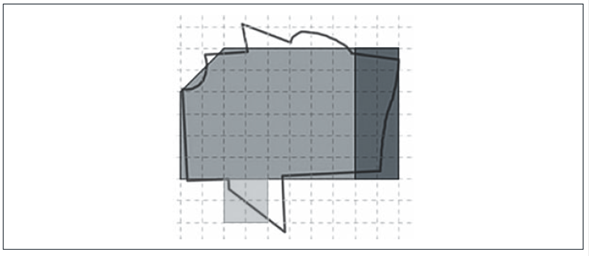
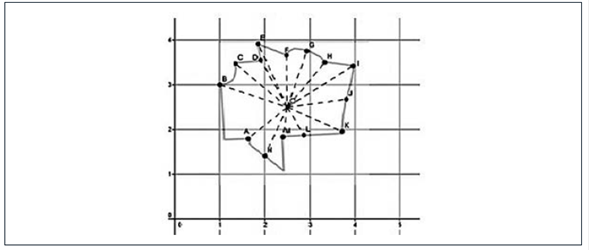
Esta técnica, como su nombre lo indica, consiste en asignar coordenadas a cada uno de los vértices que componen el polígono o la poligonal que representa el terreno. Una vez que se tienen las coordenadas de cada vértice se procede a efectuar el cálculo del área por medio de determinantes, conocida como Gauss Jordan. Generalmente se asignan las coordenadas con datos del terreno (como la altura o distancia a cierto punto de referencia), sin embargo, los profesores asignan las coordenadas de manera “arbitraria”. César y Horacio usan esta técnica para calcular el área del terreno que contiene un lago. Horacio asignó coordenadas generales (ver figura 34) y César procesó la imagen y la ubicó en un plano cartesiano para poder determinar los valores de las coordenadas y hacer los cálculos (ver figura 35).
Thumbnail
Figura 34
Técnica de cálculo de coordenadas para el terreno con lago por Horacio
Técnica de cálculo de coordenadas para el terreno con lago por Horacio
Thumbnail
Figura 35
Técnica de cálculo de coordenadas para el terreno con lago por César
Técnica de cálculo de coordenadas para el terreno con lago por César
En el planteamiento de Horacio, AT es el área total de la figura 34, AL es el área del lago y AF el área final que se quiere calcular, es decir, el área de tierra firme.
e1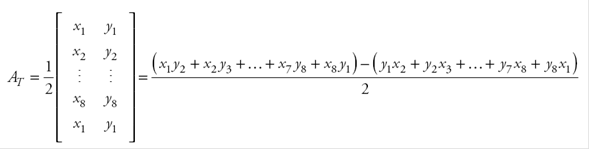
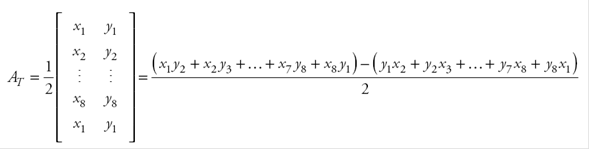
e2

César al hacer los cálculos obtiene 40.16 u2, que al analizarlos tienen una aproximación bastante buena.
Cálculo de áreas por medio de la construcción de círculos
Esta técnica consiste en ubicar un punto lo más cercano al centro del terreno considerado, luego trazar un radio cada 10 grados, a puntos del terreno (36 radios, de diferentes circunferencias), sumar los radios y promediarlos, el resultado es el radio de la circunferencia que se supone representa el área del terreno. Finalmente, se calcula el área de dicha circunferencia. Esta técnica está diseñada para el cálculo de áreas de terrenos “muy irregulares” y no muy extensos (ya que discrimina la curvatura de la tierra).
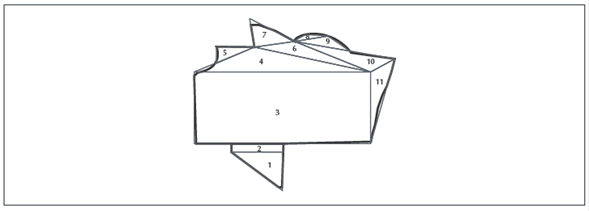
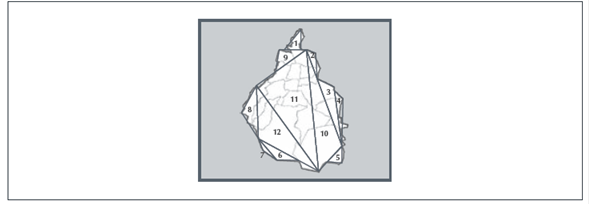
María usa esta técnica para calcular el área del terreno plano, traza radios a puntos “arbitrarios” y se guía por los vértices que representa la figura, adaptándola “no muy fortuitamente” (ver figura 36). Horacio la usa para calcular el área de la Ciudad de México, tal como se describió más arriba y como usa en Topografía, trazando los 36 radios, promediando y calculando el área de la circunferencia (ver figura 37).
Thumbnail
Figura 36
Técnica de trazo de radios para terreno plano por María
Técnica de trazo de radios para terreno plano por María
Thumbnail
Figura 37
Técnica de trazo de radios en la figura de la Ciudad de México por Horacio
Técnica de trazo de radios en la figura de la Ciudad de México por Horacio
Es importante señalar que en el curso se analizó con los profesores, las técnicas que ellos presentaron para realizar estas tareas (las adecuadas, las óptimas, las “incorrectas”), lo que mostró que considerar la realidad es complejo, pero lleva a una actividad matemática significativa, lo que tuvo un impacto en el diseño de las actividades para sus estudiantes.
Principales resultados del análisis de las técnicas de los profesores a las tareas geométrico-topográficas
El análisis previo permitió identificar que los elementos contextuales, tipo de terreno (plano, con lago, con relieves) y la forma (irregularidad) determinan la técnica más eficaz para el cálculo de áreas. Por ejemplo, en el cálculo de área de la Ciudad de México, algunos profesores calculan el área de un terreno plano, que no tiene relieves. Para ellos, da lo mismo que se diga que representa la Ciudad de México, mostrando valores numéricos completamente irreales. Por el contrario, los profesores que toman en cuenta “la realidad” del contexto, investigan técnicas utilizadas para este tipo de tareas en la Topografía (vida real) como es la de radiaciones o la de los determinantes. Asimismo, investigan la existencia de software utilizados para ello y los utilizan. Es decir, el tipo de tarea los lleva a producir técnicas que involucran conocimientos geométricos, ciertamente, pero también topográficos, informáticos y tecnológicos. Esta tarea resulta ser la más importante ya que muestra una actividad matemática rica en la que la precisión juega un rol determinante para controlar la va- lidez de la técnica. En las otras dos tareas aparece otro elemento de realidad, la representación de un lago y un contorno irregular, que lleva a varios de los profesores a generar técnicas que permitan el cálculo del área, cuadriculaciones finas, compensaciones, trazo de figuras geométricas, elección de la escala y de la unidad de medida. Esto muestra cómo la geometría de la precisión tiene una razón de ser importantísima, pero no por sí misma, sino porque permite resolver tareas reales. Obviar el lago, usar la misma técnica en tipos de tareas diferentes puede ser un efecto del paradigma tradicional en la enseñanza, “una vez que identifiques una técnica óptima la usas si las tareas se parecen un poco: cálculo de áreas”. Para mostrar cómo la realización de estas tareas les permitió a los profesores identificar las potencialidades, pero también la complejidad de proponer tareas en contextos reales, se presentan los diseños de los equipos 1 y 2.
El equipo 1 elaboró un diseño para el tratamiento de la función exponencial en el bachillerato. Éste se presenta en las figuras 38 y 39.
Thumbnail
Figura 38
Tareas 1, 2 y 3 del diseño del equipo 1
Tareas 1, 2 y 3 del diseño del equipo 1
Thumbnail
Figura 39
Tarea 4 del diseño del equipo 1
Tarea 4 del diseño del equipo 1
Como se observa, este equipo de profesores contextualizó la función exponencial en la medicina, particularmente en el tratamiento del cáncer. Para ello, buscan acercar a los estudiantes a este contexto a través del tráiler de una película y de una lectura (tareas 1 y 2). En las tareas 3 y 4 se presenta la exponencial como un modelo matemático de tiempo de vida del Radón 222 y el crecimiento de células cancerígenas. Se observa que estos modelos sólo representan una parte de los comportamientos del Radón 222 y del crecimiento de células cancerígenas y que un análisis más fino es necesario para asegurar el uso real de los modelos en medicina. Sin embargo, estos profesores comienzan a buscar tareas en contextos extra-escolares (de la vida) para dar sentido a la enseñanza del modelo exponencial.
Por su parte, el equipo 2, planteó un diseño basado en el contexto de corte y confección, como se observa en la figura 40. La actividad está planteada para estudiantes de nivel secundaria y bachillerato. Los conocimientos que se pretenden movilizar son los de proporcionalidad. Sin embargo, la técnica óptima no se apoya en la proporcionalidad ya que no se trata de hacer un dibujo a escala, sino de trazar un dibujo en el que la longitud varía, pero no proporcionalmente. La tarea propuesta, sin embargo, permitirá generar técnicas matemáticas y no-matemáticas (por ejemplo, cómo determinar la sisa y el cuello si se modifica la longitud del chaleco) validadas por conocimientos contextuales (de corte y confección).
Thumbnail
Figura 40
Tareas 1 y 2 del diseño del equipo 2
Tareas 1 y 2 del diseño del equipo 2
En estos diseños puede percibirse una primera apropiación de la metodología expuesta en la sección 3, eligen un contexto, lo analizan y buscan una relación de las matemáticas de éste con las escolares. Es decir, estos dos equipos identificaron tareas no matemáticas (en contextos de medicina y corte y confección) que permiten movilizar técnicas, validaciones y justificaciones matemáticas y contextuales. Se considera que en estos diseños subyace la idea de que conocer la utilidad de las matemáticas requiere seguir una ruta metodológica compleja, pero insoslayable para la formación de ciudadanos competentes matemáticos.
Conclusiones
El curso presentado permitió mostrar un camino para comunicar, una propuesta teórica-metodológica para el diseño de actividades didácticas, en un programa de profesionalización docente. Un elemento clave del curso fue proponer la actividad didáctica topográfica-geométrica a los profesores, para que al enfrentarla pudieran experimentar la potencialidad de las tareas, determinar el área de terrenos planos, determinar el área de terrenos con un lago y determinar el área de la Ciudad de México, ya que éstas provocan la generación de una diversidad de técnicas geométricas normadas por la precisión. Estas técnicas: cuadriculación, trazo de figuras conocidas, radiación, determinantes, trazo de polígonos de numerosos lados y cálculo de su área usando software, requieren tomar en cuenta el tipo de terreno, la unidad de medida, la escala, las propiedades de figuras geométricas conocidas, las propiedades de polígonos irregulares, los medios a disposición (papel milimétrico, software) y el grado de aproximación al “valor buscado”.
Además de realizar la actividad didáctica topográfica-geométrica y analizar los elementos antes mencionados, los profesores acceden a los elementos teóricos que subyacen al diseño, generan un nuevo diseño y lo implementa con estudiantes. Todo esto los lleva a cuestionar el paradigma tradicional, centrado en conceptos, definiciones y mecanización de técnicas, y a considerar que una manera de modificarlo es utilizar las herramientas teóricas-metodológicas puestas a su disposición, para generar una enseñanza más rica cuya razón de ser esté asociada al uso de las matemáticas en situaciones reales.
Referencias
- Artigue, M. (2011). Les défits de l’enseignment de mathématiques dan l’education de base. UNESCO: París Links
- Castela, C. y Romo-Vázquez, A. (2011). Des Mathématiques A L’Automatique: Etude des effets de transposition sur la transformée de Laplace dans la formation des ingénieurs. Recherches en Didactique des Mathématiques, 31(1), 79-130. Links
- Chevallard, Y. (1999). L’analyse des pratiques enseignantes en théorie anthropologique du didactique. Rechcerches en Didactique des Mathématiques, 19 (2), 221-266. Links
- Chevallard, Y. (1992). Concepts fondamentaux de la didactique : Perspectives apportées par une approche anthropologique. Recherches en didactique des mathématiques, 12(1), 73-112. Links
- Covián, O y Romo-Vázquez, A. (2014). Modelo Praxeológico Extendido una Herramienta para Analizar las Matemáticas en la Práctica: el caso de la vivienda Maya y el levantamiento y trazo topográfico. Bolema, 28(48), pp. 128-148. Links
- Covián, O. (2013). La formación matemática de futuros profesionales técnicos en construcción. Tesis de doctorado no publicada. México: CINVESTAV-IPN. Links
- Fuenlabrada, S. (2007). Geometría y Trigonometría (Tercera ed.). D.F., México: Mc Graw Hill. Links
- Lave, J. (1988). La cognición en la Práctica. Ediciones Paidós Ibérica. Links
- Macias, M. (2012). Uso de las nuevas tecnologías en la formación matemática de ingenieros. Tesis de maestría no publicada. México: CICATA-IPN. Links
- OECD (2016). PISA 2015 Mathematics Framework. In PISA 2015 Assessment and Analytical Framework: Science, Reading, Mathematic and Financial Literacy, OECD Publishing, París. DOI: http://dx.doi.org/10.1787/9789264255425-5-en Links
- Pérez de Moya, J. (1573). Tratado de Geometría Prácticas y Especulativa. Observatorio de Marina de San Fernando y con licencia y privilegio Real de los Reinos de Castilla y Aragón. Links
- Scott, D. & Scott, S. (2010). Innovations in the Use of Technology and Teacher Professional Development. In J. O. Lindberg & A.D. Olofsson (Eds.), Online Learning Communities and Teacher Professional Development: Methods for Improved Education Delivery (pp. 169-189). Hershey, New York: Information Science Reference. Links
- Tirosh, D. (2009). What do we know about mathematics teacher education? What evidence do we have? What comes next? Journal Mathematics Teacher Education, 12, 83-87. Links
- UNESCO. (2014). Programas y Presupuesto Aprobados (37 C/5). Recuperado de http://unesdoc.unesco.org/images/0022/002266/226695s.pdf Links
- Velasco, G. (2010). Geomtería y Trigonometría. Ciudad de México, México: Trillas. Links
- Zamora, S., Vázquez, G. y Sánchez, L. (2007). Matemáticas 2: Geometría y Trigonometría. D.F., México: ST Editorial. Links
- Zúñiga, J. A., Zúñiga, E., & Zúñiga, H. I. (2012). Geometría y Trigonometría: Formación basada en competencias, valores y desarrollo de secuencias didácticas. Ciudad de México, México: IURE Editores. Links